福建省三明市2015年普通高中毕业班质量检查理科数学试卷

'2015年三明市普通高中毕业班质量检查理科数学本试卷分第I卷(选择题)和第II卷(非选择题)，第II卷第21题为选考题，其他题为必考题．本试卷共6页．满分150分．考试时间120分钟．注意事项：1．答题前，考生先将自己的姓名、准考证号填写在答题卡上．2．考生作答时，将答案答在答题卡上．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案无效．在草稿纸、试题卷上答题无效.3．选择题答案使用2B铅笔填涂，如需改动，用橡皮擦干净后，再选涂其他答案标号；非选择题答案使用0．5毫米的黑色中性(签字)笔或碳素笔书写，字体工整、笔迹清楚．4．做选考题时，考生按照题目要求作答，并用2B铅笔在答题卡上把所选题目对应的题号涂黑．5．保持答题卡卡面清洁，不折叠、不破损．考试结束后，将本试卷和答题卡一并交回．参考公式：样本数据，，…，的标准差锥体体积公式　　其中为样本平均数其中S为底面面积，h为高柱体体积公式球的表面积、体积公式，其中S为底面面积，h为高其中R为球的半径第Ⅰ卷（选择题共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合，，那么等于A．　　　　　　　　　　B． 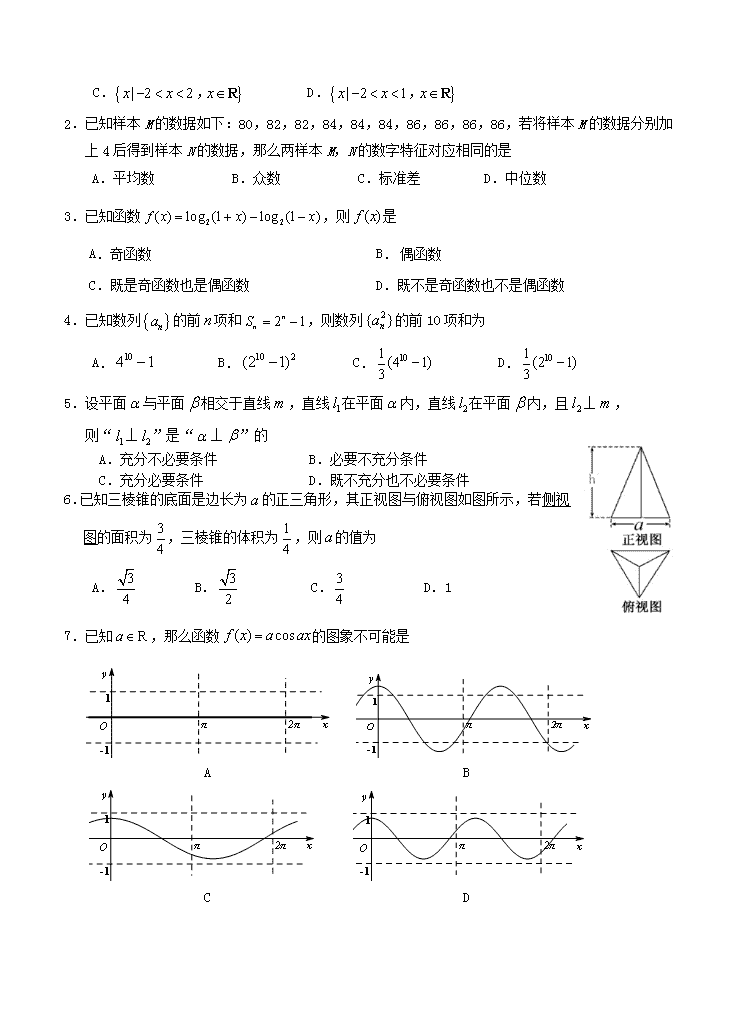C．　　　D．2．已知样本M的数据如下：80，82，82，84，84，84，86，86，86，86，若将样本M的数据分别加上4后得到样本N的数据，那么两样本M，N的数字特征对应相同的是A．平均数　B．众数C．标准差D．中位数3．已知函数，则是　A．奇函数B．偶函数　C．既是奇函数也是偶函数D．既不是奇函数也不是偶函数4．已知数列的前项和，则数列的前10项和为A．　B．C．D．5．设平面与平面相交于直线，直线在平面内，直线在平面内，且⊥，则“⊥”是“⊥”的A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件6．已知三棱锥的底面是边长为的正三角形，其正视图与俯视图如图所示，若侧视图的面积为，三棱锥的体积为，则的值为A．　　　　B．　　　　C．　　　　　D．17．已知，那么函数的图象不可能是　A　　　　　　　　　　　　　　　　　　B　C　　　　　　　　　　　　D 8．已知函数将函数的零点按从小到大的顺序排列，构成数列，则该数列的通项公式为A．B．C．D．an＝2n－29．已知区域，区域，在内随机投掷一点，则点落在区域内的概率是A．　　B．　　C．　　D．10．若曲线在点处切线的斜率为，曲线在点处切线的斜率为（），将的值称为这两曲线在，间的“异线曲度”，记作．现给出以下四个命题：①已知曲线，，且，则；②存在两个函数，，其图像上任意两点间的“异线曲度”为常数；③已知抛物线，，若，则；④对于曲线，，当时，若存在实数，使得恒成立，则的取值范围是．其中正确命题的个数是A．1B．2C．3D．4第Ⅱ卷（非选择题共100分） 二、填空题:本大题共5小题，每小题4分，共20分．把答案填在答题卡相应位置．11．二项式的展开式中，的系数是，则实数＝_____．12．某学校为调查高中三年级男生的身高情况，选取了名男生作为样本，右图是此次调查统计的流程图，若输出的结果是，则身高在以下的频率为＿＿＿＿＿．13．若命题“”为假命题，则实数的取值范围是．14．过双曲线的一个焦点作一条渐近线的垂线，若垂足恰在线段(为原点)的垂直平分线上，则双曲线的离心率为．15．如图，三条平行直线把平面分成①、②、③、④四个区域（不含边界），且直线到的距离相等．点在直线上，点在直线上，为平面区域内的点，且满足．若所在的区域为④,则的取值范围是是．三、解答题：本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤.16.（本小题满分13分）已知集合，从中随机抽取两个不同的元素，作为复数(为虚数单位)的实部和虚部．（Ⅰ）求复数在复平面内的对应点位于第一象限的概率；（Ⅱ）设，求的分布列及其数学期望.17．（本小题满分13分）如图1，在矩形中，，，将沿矩形的对角线 翻折，得到如图2所示的几何体，使得＝．(Ⅰ)求证：；(Ⅱ)若在上存在点，使得，求二面角的余弦值．图1图218.（本小题满分13分）已知点在以为右焦点的椭圆上，斜率为1的直线过点与椭圆交于两点，且与直线交于点．(Ⅰ)求椭圆的离心率；(Ⅱ)试判断直线，，的斜率是否成等差数列？若成等差数列，给出证明；若不成等差数列，请说明理由．19．（本小题满分13分）如图是某种可固定在墙上的广告金属支架模型，其中，是的中点，，设，且．(Ⅰ)若，求的长；(Ⅱ)求的长，并求的最小值；(Ⅲ)经市场调查发现，某地对该种金属支架的需求量与有关，且需求量的函数关系式为（单位：万件），试探究是否存在某种规格 的金属支架在当地需求量为零？并说明理由．20．（本小题满分14分）已知函数．（Ⅰ）当时，求函数的单调区间；（Ⅱ）当时，函数图象上的点都在所表示的平面区域内，求实数的取值范围．（Ⅲ）将函数的导函数的图象向右平移一个单位后，再向上平移一个单位，得到函数的图象，试证明：当时，．21．本题有（1）、（2）、（3）三个选答题，每题7分，请考生任选2题作答，满分14分．如果多做，则按所做的前两题记分．作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中．（1）（本小题满分7分）选修4－2：矩阵与变换已知矩阵（）．（Ⅰ）当时，求矩阵的特征值以及属于每个特征值的一个特征向量；（Ⅱ）当时，曲线在矩阵的对应变换作用下得到曲线：，求的值．（2）（本小题满分7分)选修4—4：极坐标与参数方程在平面直角坐标系中，已知直线的参数方程为(为参数)．以直角坐标原点 为极点，轴的非负半轴为极轴建立极坐标系，曲线的极坐标方程为．（Ⅰ）求曲线的直角坐标方程；（Ⅱ）若是直线与曲线的内部的公共点，求的取值范围．（3）（本小题满分7分)选修4—5：不等式选讲已知不等式的解集与不等式的解集相同．（Ⅰ）求，的值；（Ⅱ）求函数的最大值及取得最大值时的值．2015年三明市普通高中毕业班质量检查理科数学试题参考答案及评分标准一．选择题：　　1—5BCACB　　6—10DDABC二、填空题：11．；　12．；　13．；　14．；　15．；三．解答题：16．解：（Ⅰ）从集合中随机抽取两个不同的元素，组成复平面内的对应点有种，其中位于第一象限的点有种，所以所求的概率为.　　　……………………6分（Ⅱ）,．　　　　　　……………………7分,，，．251013　　　　　　　　　　　　　　　　　　　……………………11分 ∴.……………………13分17．解：（Ⅰ）当时，，，∴，又，∴平面，而平面，∴．　　　　……………………5分（Ⅱ）如图，以为原点，所在直线为轴，所在直线为轴，建立空间直角坐标系，由（Ⅰ）知，又，∴平面，∵平面，∴平面⊥平面，过作，则轴，　　　　　　　　……………………7分在中，，，可得．故，∵，∴为中点，∴．设平面的法向量为，则∴　即……………9分取，则，又平面的法向量为，………11分则＝＝．故二面角的余弦值为．　　　　……………………13分18．解：（Ⅰ）因为点在椭圆上，所以.整理得，，即，解得或(舍)，所以离心率.　　　　　　　……………………5分（Ⅱ）直线，，的斜率成等差数列，证明如下： 由(Ⅰ）知，，∴椭圆直线的方程为．代入椭圆方程并整理，得.　……………………6分设，直线，，的斜率分别为k1，k2，k3，则有.　　　　　　　　　……………………8分可知的坐标为．所以，　　　　　……………………12分∴.故直线，，的斜率成等差数列．　　　……………………13分19．解法一：（Ⅰ）在中，已知，，，由正弦定理得：，故.　……………………2分当时,＝故的长为．　　　……………………4分（Ⅱ）在中，已知，，，由余弦定理得：　　　……………………5分 　　　　　　……………………7分因为，所以，即，则的最小值为，此时=1，即.　　……………………9分(用其它方法求出的表达式及最小值酌情给分)（Ⅲ）设x=6θ,,令,,问题转化为在是否存在的值，使是,　　　　……………………10分①当时,|sinx|≤1，必有；②当时,，因为，所以，从而,在恒成立，在区间递减，于是综上，在,恒成立，故不存在某种规格的金属支架,在当地需求量为零.　　　　　　　　　　……………………13分解法二：（Ⅰ），（Ⅱ）同解一．（Ⅲ）设x=6θ,，令,,　　 问题转化为在是否存在x的值，使得使是,　………………10分,令，得,∵,故存在,,使得,易知在单调递，在(递减，在递增，故在,,∵,注意到,且,∴,．这样．……………12分综上：在,恒成立，故不存在某种规格的金属支架,在当地需求量为零．　　　　　　　　　　　　　　……………………13分20．解法一：（Ⅰ）当时，，，故函数的单调递增区间为.……………………3分（Ⅱ）因函数图象上的点都在所表示的平面区域内，则当时，不等式恒成立，即恒成立，、设()，只需即可．由，　　　　　　…………………4分(ⅰ)当时，， 当时，，函数在上单调递减，故成立．　　　　　　　　　　　　　……………………5分(ⅱ)当时，由，因，所以，①若，即时，在区间上，，则函数在上单调递增，在上无最大值，当时，，此时不满足条件；②若，即时，函数在上单调递减，在区间上单调递增，同样在上无最大值，当时，，不满足条件．　　　　　　　　　……………………7分(ⅲ)当时，由，∵，∴，∴，故函数在上单调递减，故成立．……………………8分综上所述，实数的取值范围是．……………………9分（Ⅲ），∴，当时，　　　　…………………10分∴.令，则.∵，∴. ∴，即.　　　　　　……………………14分解法二：（Ⅰ），（Ⅱ）同解一．（Ⅲ），∴，当时，，…………………10分∴设，当时，结论成立；当时，∵当时，∴，当时，上式显然成立.∴当时，；当时，∴∴，.　　　……………………14分解法三：（Ⅰ），（Ⅱ）同解一．（Ⅲ），∴，当时，　　　…………………10分∴以下用数学归纳法证明不等式. ①当时，左边，右边，不等式成立；②假设当时，不等式成立，即，则.也就是说，当时，不等式也成立.由①②可得，对，都成立.………………14分21．（1）解：（Ⅰ），令＝＝0，得或，当时，由，得，当时，由，得，所以对应特征值为2的一个特征向量是；对应特征值为3的一个特征向量是．　　　　……………………4分（Ⅱ）设曲线上的点在矩阵的作用下变成，则，即将变换公式代入曲线：可得，，即，即为曲线，∴，又，∴．　　　　　……………………7分 （2）解法一：（Ⅰ）∵，∴，∴，即，所以曲线的直角坐标方程为．　　　……………………4分（Ⅱ）法一：∵，而，∴，∴，即的范围是．……………………7分解法二：（Ⅰ）同解法一．（Ⅱ）联立解得或∴的范围是．　　　　……………………7分（3）解：（Ⅰ）不等式的解集为，所以方程的两根为.∴解得.　　　　　……………………4分（Ⅱ）由（Ⅰ）可知，＝，定义域为.所以.则，当且仅当时取等号. 故当时，的最大值为.　　　…………………7分欢迎访问“高中试卷网”——http://sj.fjjy.org'