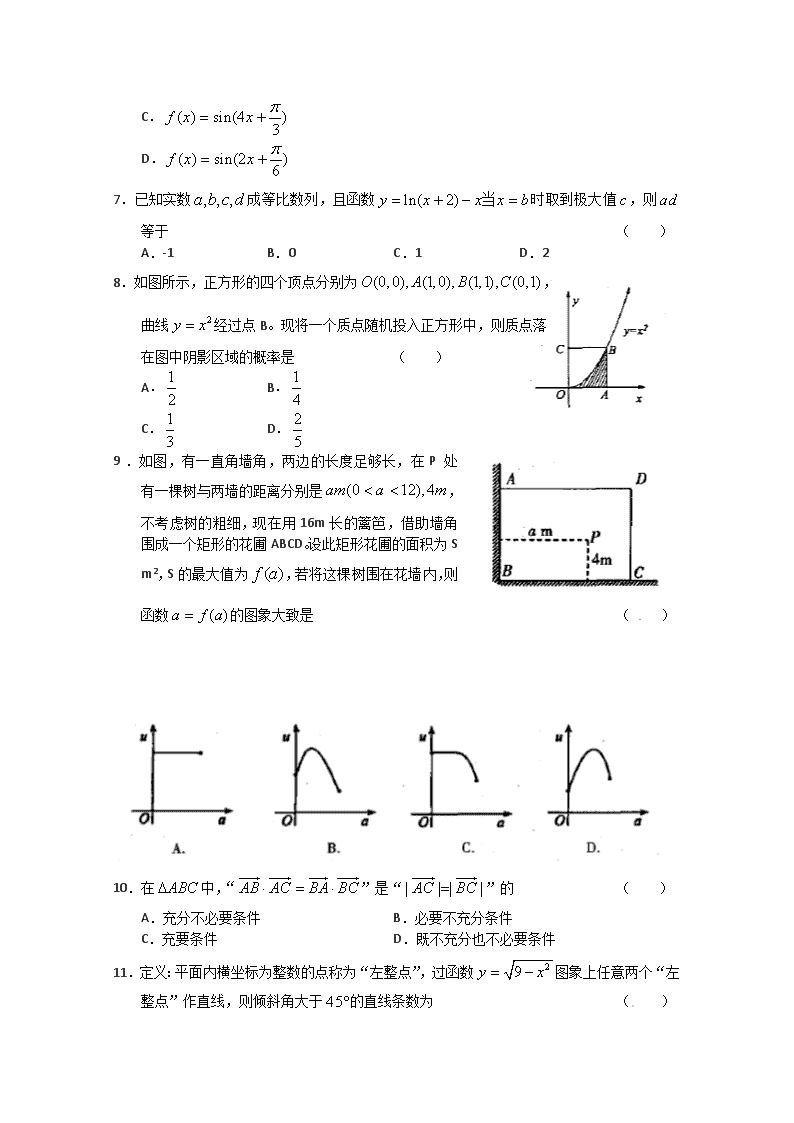
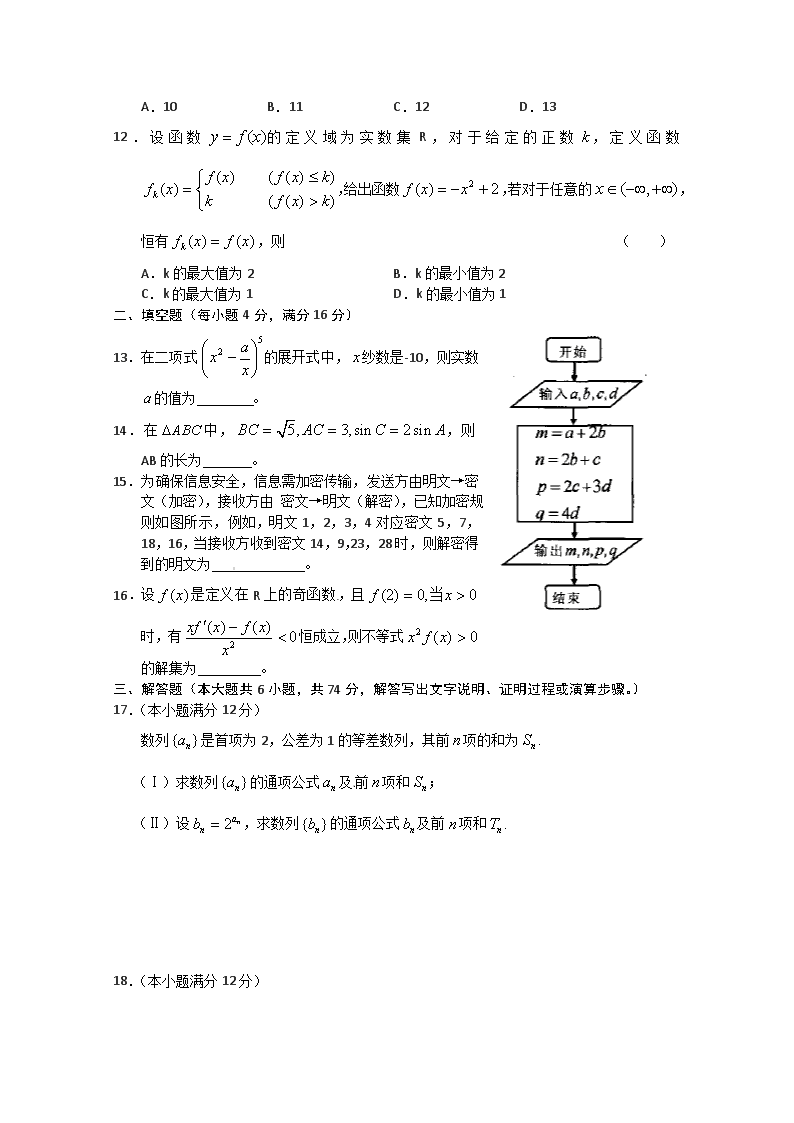
- 782.00 KB
- 11页
- 1、本文档共5页,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,可选择认领,认领后既往收益都归您。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形,可联系本站下载客服投诉处理。
- 文档侵权举报电话:19940600175。
'福建省福州市2011届高三上学期期末质量检查数学试题(理科)(满分:100分;完卷时间:90分钟)友情提示:答案一律填写在答题卡上。一、选择题(每小题5分,满分60分)1.已知集合等于()A.(0,1),(1,2)B.{(0,1),(1,2)}C.D.2.设复数等于()A.-3B.3C.D.3.如图是歌手大奖赛中,七位评委为甲,乙两名选手打出的分数的茎叶图(其中为数字0—9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为,则一定有()A.B.C.D.的大小不确定4.已知实数满足的最小值为()A.2B.3C.4D.55.若双曲线的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为()A.B.5C.D.26.设函数的部分图象如图所示,直线是它的一条对称轴,则函数的解析式为()A.B.
C.D.7.已知实数成等比数列,且函数时取到极大值,则等于()A.-1B.0C.1D.28.如图所示,正方形的四个顶点分别为,曲线经过点B。现将一个质点随机投入正方形中,则质点落在图中阴影区域的概率是()A.B.C.D.9.如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是,不考虑树的粗细,现在用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD。设此矩形花圃的面积为Sm2,S的最大值为,若将这棵树围在花墙内,则函数的图象大致是()10.在中,“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件11.定义:平面内横坐标为整数的点称为“左整点”,过函数图象上任意两个“左整点”作直线,则倾斜角大于的直线条数为()
A.10B.11C.12D.1312.设函数的定义域为实数集R,对于给定的正数,定义函数,给出函数,若对于任意的,恒有,则()A.k的最大值为2B.k的最小值为2C.k的最大值为1D.k的最小值为1二、填空题(每小题4分,满分16分)13.在二项式的展开式中,纱数是-10,则实数的值为。14.在中,,则AB的长为。15.为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则如图所示,例如,明文1,2,3,4对应密文5,7,18,16,当接收方收到密文14,9,23,28时,则解密得到的明文为。16.设是定义在R上的奇函数,且时,有恒成立,则不等式的解集为。三、解答题(本大题共6小题,共74分,解答写出文字说明、证明过程或演算步骤。)17.(本小题满分12分)数列是首项为2,公差为1的等差数列,其前项的和为(Ⅰ)求数列的通项公式及前项和;(Ⅱ)设,求数列的通项公式及前项和18.(本小题满分12分)
已知函数的最小正周期为(Ⅰ)求的值;(Ⅱ)求函数在区间上的取值范围。19.(本小题满分12分)一个袋子内装有若干个黑球,3个白球,2个红球(所有的球除颜色外其它均相同),从中一次性任取2个球,每取得一个黑球得0分,每取一个白球得1分,每取一个红球得2分,用随机变量表示取2个球的总得分,已知得0分的概率为(Ⅰ)求袋子内黑球的个数;(Ⅱ)求的分布列与期望。20.(本小题满分12分)某货轮匀速行驶在相距300海里的甲、乙两地间运输货物,运输成本由燃料费用和其它费用组成,已知该货轮每小时的燃料费用与其航行速度的平方成正比(比例系数为0.5),其它费用为每小时800元,且该货轮的最大航行速度为50海里/小时。(Ⅰ)请将从甲地到乙地的运输成本y(元)表示为航行速度(海里/小时)的函数;(Ⅱ)要使从甲地到乙地的运输成本最少,该货轮应以多大的航行速度行驶?
21.(本小题满分12分)(文题满分14分)如图,为半圆,AB为半圆直径,O为半圆圆心,且,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变。(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;(Ⅱ)过点B的直线与曲线C交于M、N两点,与OD所在直线交于E点,若为定值。22.(本小题满分14分)已知函数在(-∞,0)上是减函数,在(0,1)上是增函数,函数在R上有三个零点,且1是其中一个零点。(Ⅰ)求的值;(Ⅱ)求的取值范围;(Ⅲ)设,且的解集为(-∞,1),求实数的取值范围。
参考答案一、选择题(每小题5分,满分60分)1.D2.A3.B4.A5.A6.D7.A8.C9.C10.C11.B12.B二、填空题(每小题4分,满分16分)13.114.15.6,4,1,716.(-∞,-2)∪(0,2)三、解答题(本大题共6小题,共74分.解答写出文字说明、证明过程或演算步骤.)17.(本小题满分12分)解:(Ⅰ)依题意:2分=4分(Ⅱ)由(Ⅰ)知5分7分9分12分18.(本小题满分12分)解:(Ⅰ)2分5分因为函数的最小正周期为,且,
所以,解得.7分(Ⅱ)由(Ⅰ)得因为,所以,9分所以,因此,即的取值范围为.12分19.(本小题满分12分)解:(Ⅰ)设袋中黑球的个数为n,由条件知,当取得2个黑球时得0分,概率为:2分化简得:,解得或(舍去),即袋子中有4个黑球4分(Ⅱ)依题意:=0,1,2,3,45分6分7分8分∴的分布列为10分12分
20.(本小题满分12分)解:(Ⅰ)由题意,每小时的燃料费用为,从甲地到乙地所用的时间为小时,2分则从甲地到乙地的运输成本,6分故所求的函数为,.7分(Ⅱ)由(1),9分当且仅当,即时取等号.…11分故当货轮航行速度为40海里/小时时,能使该货轮运输成本最少.12分21.(本小题满分12分)(文22题满分14分)解:(Ⅰ)以AB、OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系,∵动点P在曲线C上运动且保持|PA|+|PB|的值不变.且点Q在曲线C上,∴|PA|+|PB|=|QA|+|QB|=2>|AB|=4.∴曲线C是为以原点为中心,A、B为焦点的椭圆设其长半轴为a,短半轴为b,半焦距为c,则2a=2,∴a=,c=2,b=1.∴曲线C的方程为+y2=15分(Ⅱ)证法1:设点的坐标分别为,又易知点的坐标为.且点B在椭圆C内,故过点B的直线l必与椭圆C相交.∵,∴.∴,.7分将M点坐标代入到椭圆方程中得:,去分母整理,得.10分同理,由可得:.∴,是方程的两个根,∴.12分
(Ⅱ)证法2:设点的坐标分别为,又易知点的坐标为.且点B在椭圆C内,故过点B的直线l必与椭圆C相交.显然直线的斜率存在,设直线的斜率为,则直线的方程是.将直线的方程代入到椭圆的方程中,消去并整理得.8分∴,.又∵,则.∴,同理,由,∴.10分∴.12分22.(本小题满分14分)解:(Ⅰ)∵f(x)=-x3+ax2+bx+c,∴.1分∵f(x)在在(-∞,0)上是减函数,在(0,1)上是增函数,∴当x=0时,f(x)取到极小值,即.∴b=0.3分(Ⅱ)由(1)知,f(x)=-x3+ax2+c,∵1是函数f(x)的一个零点,即f(1)=0,∴c=1-a.5分∵的两个根分别为,.∵f(x)在(0,1)上是增函数,且函数f(x)在上有三个零点,∴,即.7分∴.故f(2)的取值范围为.9分(Ⅲ)解法1:由(Ⅱ)知,且.
∵1是函数的一个零点,∴,∵∴,∴点是函数和函数的图像的一个交点.10分结合函数和函数的图像及其增减特征可知,当且仅当函数和函数的图像只有一个交点时,的解集为.即方程组(1)只有一个解.11分由,得.即.即.∴或.12分由方程,(2)得.∵,当,即,解得13分此时方程(2)无实数解,方程组(1)只有一个解.所以时,的解集为.14分(Ⅲ)解法2:由(Ⅱ)知,且.∵1是函数的一个零点又的解集为,10分11分
12分14分www.ks5u.com'
您可能关注的文档
- 2006年永春县初中毕业班教学质量检查(数学)
- 2005年泉州市初中教学质量检查(新课改)试题
- 凤城中学教研片2011-2012学年初三语文第一学期期中质量检查卷
- 安徽省蚌埠市2013届高三第二次教学质量检查考试语文试题详解
- 2013年漳州市初中毕业班质量检查数学试卷解析及解析检测题测试题解析北师大版
- 2008-2009学年初一数学下册期中考试质量检查卷
- 福州一中2011-2012学年高三语 文(下)质量检查试题卷
- 2007年泉州市高中毕业班理科质量检查数学试题,试卷
- 福建省2015年普通高中毕业班4月质量检查语文
- 2009年高三理科数学普通高中毕业班质量检查模拟试卷及答案【福建省宁德市】
- 2009届高三理科数学毕业班质量检查模拟试题及答案【湖北省荆州市】
- 2006年暑假广东广雅中学高三升学辅导班质量检查试题数学(文科)
- 2009届高三文科数学毕业班质量检查模拟试题及答案【湖北省荆州市】
- 2011届福建漳州市初中毕业班数学质量检查试卷及答案
- 2005年福建省泉州市初中教学质量检查(省级课改实验区)数学试题试题
- 2009年高三文科数学普通高中毕业班质量检查模拟试卷及答案【福建省宁德市】
- 2010年福建省福州市初中毕业班质量检查考试数学试题及答案(扫描)
- 2011届福建福州市高三上学期期末数学文科质量检查试题及答案