杨氏模量不确定度的评定方法

'第26卷第5期吉林建筑工程学院学报Vo1．26No．52009年10月JournalofJilinInstituteofArchitecture&CiviIEngineeringOct．2009杨氏模量不确定度的评定方法宋晓东(吉林建筑工程学院基础科学部，长春130021)摘要：在拉伸法测金属丝的杨氏弹性模量实验中，对结果的不确定度的评定一般有多种方法．笔者讨论了教学中用逐差法处理数据时不确定度的简化评定方法：单次测量量根据具体实验条件进行估计，多次测量量采用合成法．关键词：杨氏模量：不确定度；逐差法中图分类号：0433文献标识码：A文章编号：1009-0185(2009)05-0100-03EvaluationMethodoftheUncertaintyofYoung’SModulusSONGXiao—。dong(DepartmentofBasicScience，JilinInstituteofArchitectureandCivilEngineering，Changchun，China130021)Abstract：IntheexperimentofmeasuringYoung’Selasticitymodulusofmetalfilamentbyusingtensilemethod，gen·erallythereareanumberofwaystomeasuretheresultsoftheevaluationofuncertainty．Thispapermainlydiscussesthesimplifiedevaluationofuncertaintywhichprocessedbymethodofsuccessiveminusinteaching：measuringthevolumeofasingleexperimentinaccordancewiththetermsofthespecificestimates，repeatedmeasurementusingsyn·theticmethod．Keywords：theexperimentofYoung’Smodulus；uncertainty；methodofsuccessiveminus0引言在普通物理实验中，用拉伸法测金属丝杨氏模量的数据处理一般有作图法、逐差法、最／J~--乘法．由j作图法的局限(图纸的大小、连线的任意性和连线的粗细等)，不可避免地会引入误差．而最小二乘法进行不确定度分析过程较为繁琐，对初学者较难．笔者讨论拉伸法测量金属丝的杨氏弹性模量的实验教学中用逐差法处理数据时的不确定度的简化评定方法．1拉伸法测金属丝杨氏弹性模量的原理物体在外力作用下要发生形变，当形变不超过某一限度时，撤消外力之后形变能随之消失，这种形变叫弹性形变，发生弹性形变时物体内部将产生恢复原状的内应力Ⅲ．设有一截面为S，长度为L的均匀棒状(或线状)材料，受拉力列立伸时，伸长了△￡，其单位截面所受到的拉力F／S称为应力，而单位长度的伸长量△称为应变．根据胡克定律，在弹性形变范围内，棒状(或线状)固体应变与它所受的应力成正比，其比例系数E取决于固体材料的性质，反应了材料形变和内应力之间的关系，称为杨氏弹性模量：收稿日期：2009—03—20．作者简介：宋晓东(1969~)，男，吉林省长舂市人，讲师 第5期宋晓东：扬氏模量不确定度的评定方法l0lFL也=一＆拉伸法测金属丝杨氏弹性模量的装置和原理如图1所示，其中以由所挂砝码的重量求出，截面积可通过螺旋测微计测量金属丝的直径计算得出，工可用米尺等常规测量器具测量，但△三由于其值非常微小，用常规的测量方法很难精确测量．实验将用“光杠杆豳|4-．法”来测量这一微小的长度改变量△三．和为挂砝码前后光杠卜反射镜；2一活动托台：3-周定托台：4一标尺：5一望远镜杆平面镜的位置，和玎为望远镜中先后观察到的标尺读数．由公图I光杠杆装置及测量原理式(1)和测量原理图可以得到杨氏模量的计算公式为：8LDF(2)=——：_—一6(△，，)式中，为杨氏模量；三为金属丝长度；，为对应标尺读数改变量,An的改变荷重；D为光杠杆镜面到标尺的距离；d为金属丝的直径；b为光杠杆的长度．2杨氏模量不确定度的简化评定方法2．1由计算公式导出杨氏模量的不确定度传递公式=E·(3)2．2各直接测量量的不确定度评定(1)金属丝长度三在测量时，由于有上下端的紧固夹头，通常用米尺较难测准．镜尺之间的距离D在测量时，应尽可能将钢卷尺拉成水平，所以在不确定度的估计时，考虑示值误差和读数误差，其不确定度和估计为2m．(2)的估计可由实验室给出．(3)光杠杆的长度b在测量时是将光杠杆兰足放在白纸上，用钢直尺测压痕的距离(单次测量)．钢直尺的示值误差设为均匀分布，则：：．一o．o8mm(4)3(4)金属丝的直径是用螺旋测微计多次测量，其合成不确定度为：=(5)式中，为螺旋测微计的示值误差．(5)对应荷重F标尺读数的变化量△力采用逐差法处理，其测量不确定度为：U=(6) 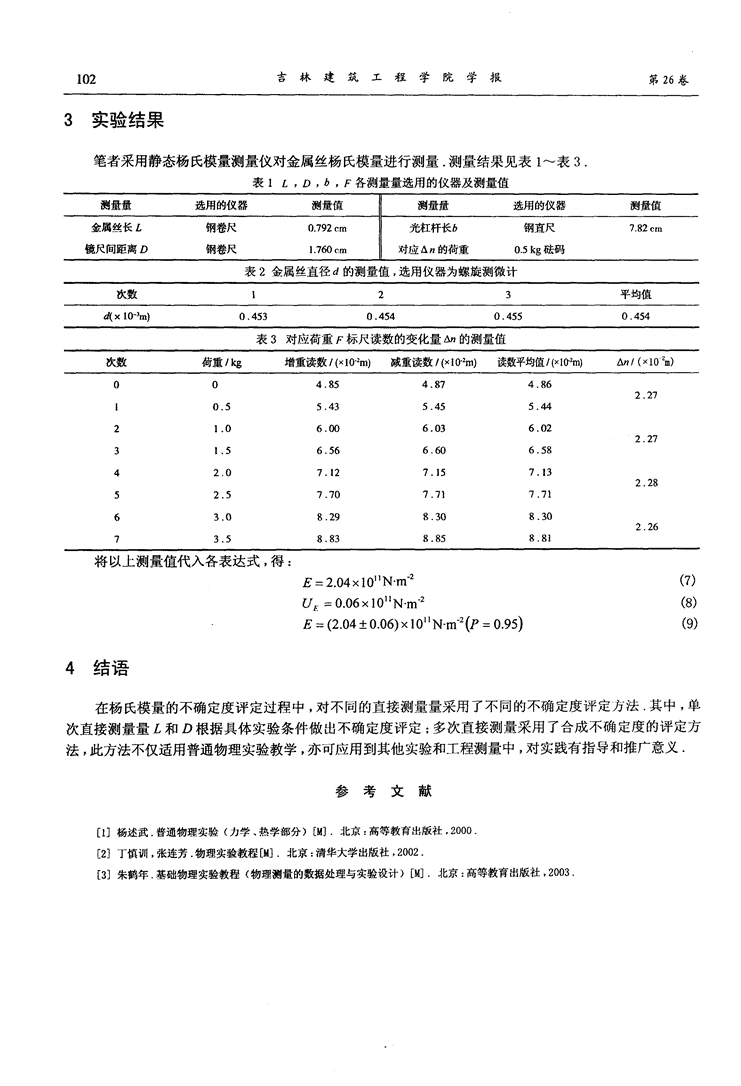102吉林建筑工程学院学报第26卷3实验结果笔者采用静态杨氏模量测量仪对金属丝杨氏模量进行测量．测量结果见表1～表3．表1￡，D，b，F各测量量选用的仪器及测量值测量量选用的仪器测量值测量量选用的仪器测量值金属丝长￡钢卷尺O．792cm光杠杆长b钢直尺7．82cm镜尺间距离D钢卷尺1．760cm对应△的荷重O．5砝码表2金属丝直径d的测量值，选用仪器为螺旋测微计将以上测量值代入各表达式，得：E：2．04×10"N·m’(7)：0．06×l0”N·m‘(8)E=(2．04_+0．05)xl0“N-m也(尸=0．95)(9)4结语在杨氏模量的不确定度评定过程中，对不同的直接测量量采用了不同的不确定度评定方法．其中，单次直接测量量￡和D根据具体实验条件做出不确定度评定；多次直接测量采用了合成不确定度的评定方法，此方法不仅适用普通物理实验教学，亦可应用到其他实验和工程测量中，对实践有指导和推广意义．参考文献[1]杨述武．普通物理实验(力学、热学部分)[．北京：高等教育出版社，2000．[2]丁慎训，张连芳．物理实验教程[M]．北京：清华大学出版社，2002．[3]朱鹤年．基础物理实验教程(物理测鼍的数据处理与实验设计)[M]．北京：高等教育出版社，2003'