2012年福州市初中毕业班质量检查数学试卷

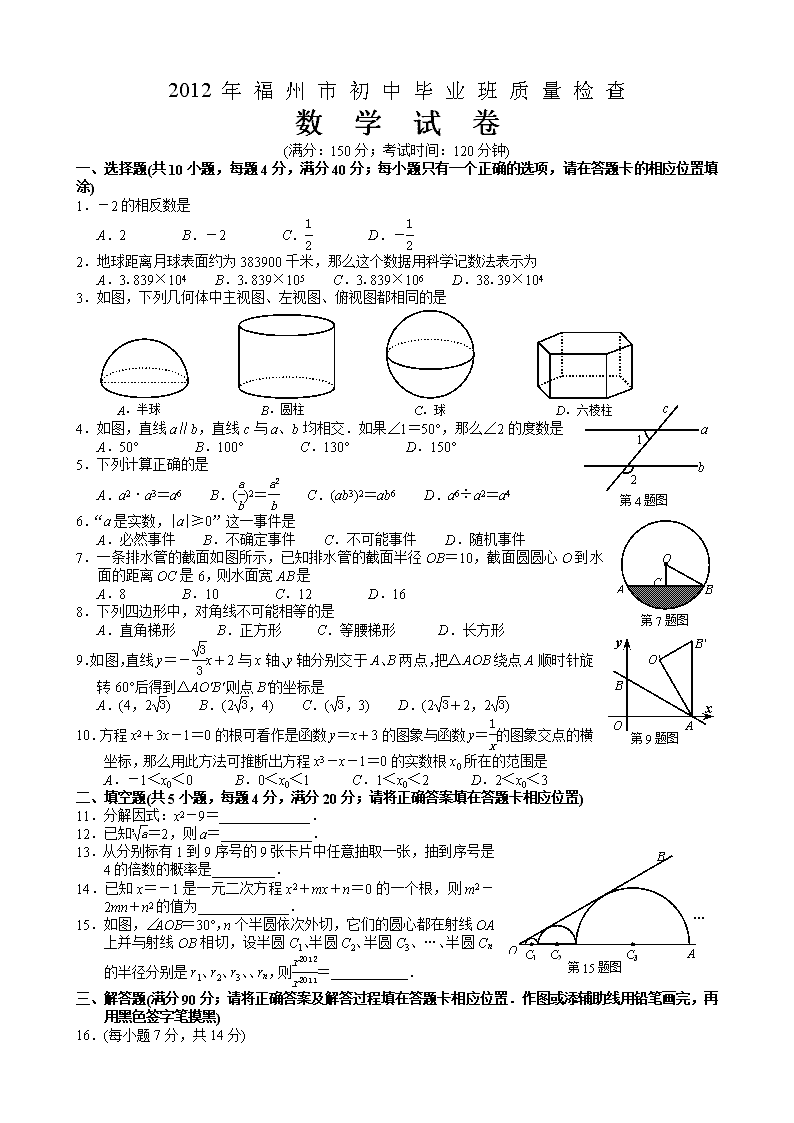
'2012年福州市初中毕业班质量检查数学试卷(满分：150分；考试时间：120分钟)一、选择题(共10小题，每题4分，满分40分；每小题只有一个正确的选项，请在答题卡的相应位置填涂)1．－2的相反数是A．2B．－2C．D．－2．地球距离月球表面约为383900千米，那么这个数据用科学记数法表示为A．3.839×104B．3.839×105C．3.839×106D．38.39×1043．如图，下列几何体中主视图、左视图、俯视图都相同的是D．六棱柱C．球B．圆柱A．半球b第4题图12ac4．如图，直线a∥b，直线c与a、b均相交．如果∠1＝50°，那么∠2的度数是A．50°B．100°C．130°D．150°5．下列计算正确的是A．a2·a3＝a6B．()2＝C．(ab3)2＝ab6D．a6÷a2＝a4ABCO第7题图6．“a是实数，|a|≥0”这一事件是A．必然事件B．不确定事件C．不可能事件D．随机事件7．一条排水管的截面如图所示，已知排水管的截面半径OB＝10，截面圆圆心O到水面的距离OC是6，则水面宽AB是A．8B．10C．12D．168．下列四边形中，对角线不可能相等的是ABOxyB"第9题图O"A．直角梯形B．正方形C．等腰梯形D．长方形9．如图，直线y＝－x＋2与x轴、y轴分别交于A、B两点，把△AOB绕点A顺时针旋转60°后得到△AO"B"，则点B"的坐标是A．(4，2)B．(2，4)C．(，3)D．(2＋2，2)10．方程x2＋3x－1＝0的根可看作是函数y＝x＋3的图象与函数y＝的图象交点的横坐标，那么用此方法可推断出方程x3－x－1＝0的实数根x0所在的范围是A．－1＜x0＜0B．0＜x0＜1C．1＜x0＜2D．2＜x0＜3二、填空题(共5小题，每题4分，满分20分；请将正确答案填在答题卡相应位置)11．分解因式：x2－9＝_____________．12．已知＝2，则a＝_____________．ABOC1C2C3第15题图…13．从分别标有1到9序号的9张卡片中任意抽取一张，抽到序号是4的倍数的概率是_________．14．已知x＝－1是一元二次方程x2＋mx＋n＝0的一个根，则m2－2mn＋n2的值为_____________．15．如图，∠AOB＝30°，n个半圆依次外切，它们的圆心都在射线OA上并与射线OB相切，设半圆C1、半圆C2、半圆C3、…、半圆Cn的半径分别是r1、r2、r3、、rn，则＝___________．三、解答题(满分90分；请将正确答案及解答过程填在答题卡相应位置．作图或添辅助线用铅笔画完，再用黑色签字笔摸黑)16．(每小题7分，共14分) (1)计算：|－1|＋＋(－3.14)0－()－1．(2)先化简，再求值：(x＋1)2＋x(x－2)，其中x＝．17．(每小题7分，共14分)ABCDαβ第17(2)题图(1)如图，在平行四边形ABCD中，E为BC中点，AE和延长线与DC的延长线相交于点F．证明：△ABE≌△FCE．ABCDEF第17(1)题图(2)如图，热气球的探测器显示，从热气球看一栋高楼顶部的仰角α为45°，看这栋高楼底部的俯角β为60°，热气球与高楼的水平距离AD＝80m，这栋高楼有多高(≈1.732，结果保留小数点后一位)？18．(满分12分)某市教育局为了了解初一学生第一学期参加社会实践活动的天数，随机抽查本市部分初一学生第一学期参加社会实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图(如图)．2030105060403天4天5天6天7天和7天以上人数时间3天4天5天6天7天和7天以上30%15%10%20%a请你根据图中提供的信息，回答下列问题：(1)a＝_______%，并写出该扇形所对圆心角的度数为_________；补全条形图；(2)在这次抽样调查中，众数和中位数分别是多少？(3)如果该市有初一学生20000人，请你估计“活动时间不少于5天”的大约有多少人？ABCDEO第19题图19．(满分11分)如图，在△ABC中，AB＝AC，以AC为直径的半圆O分别交AB、BC于点D、E．(1)求证：点E是BC的中点；(2)若∠COD＝80°，求∠BED的度数．20．(满分12分)某文化用品商店计划同时购进一批A、B两种型号的计算器，若购进A型计算器10只和B型计算器8只，共需要资金880元；若购进A型计算器2只和B型计算器5只，共需要资金380元．(1)求A、B两种型号的计算器每只进价各是多少元？(2)该经销商计划购进这两种型号的计算器共50只，而可用于购买这两种型号的计算器的资金不超过2520元．根据市场行情，销售一只A型计算器可获利10元，销售一只B型计算器可获利15元．该经销商希望销售完这两种型号的计算器，所获利润不少于620元．则该经销商有哪几种进货方案？ABCDEF第21题图21．(满分13分)如图，在△ABC中，AB＝AC＝10cm，BC＝16cm，DE＝4cm．动线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动，当端点E到达点C时运动停止．过点E作EF∥AC交AB于点F(当点E与点C重合时，EF与CA重合)，连接DF，设运动的时间为t秒(t≥0)．(1)直接写出用含t的代数式表示线段BE、EF的长；(2)在这个运动过程中，△DEF能否为等腰三角形？若能，请求出t的值；若不能，请说明理由；(3)设M、N分别是DF、EF的中点，求整个运动过程中，MN所扫过的面积．22．(满分14分)如图，已知抛物线y＝x2＋bx＋c经过A(3，0)、B(0，4)两点．(1)求此抛物线的解析式； (2)若抛物线与x轴的另一个交点为C，求点C关于直线AB的对称点C"的坐标；(3)若点D是第二象限内点，以D为圆心的圆分别与x轴、y轴、直线AB相切于点E、F、H，问在抛物线的对称轴上是否存在一点一点P，使得|PH－PA|的值最大？若存在，求出该最大值；若不存在，请说明理由．ABCOxyDEFH第22(3)题图ABCOxy第22(2)题图 2012年福州市初中毕业班质量检查数学试卷参考答案及评分标准一、选择题：1．A2．B3．C4．C5．D6．A7．D8．A9．B10．C二、填空题：11．(x＋3)(x－3)12．813．14．115．3三、解答题：16．(1)解：|－1|＋＋(－3.14)0－()－1＝1＋×2＋1－24分＝．7分(2)解：(x＋1)2＋x(x－2)＝x2＋2x＋1＋x2－2x4分＝2x2＋1，5分当x＝时，原式＝2×()2＋1＝5．7分17．(1)证明：∵AB与CD是平行四边形ABCD的对边，∴AB∥CD，2分∴∠F＝∠FAB．4分∵E是BC的中点，∴BE＝CE，5分又∵∠AEB＝∠FEC，6分∴△ABE≌△FCE．7分(2)解：如图，α＝45°，β＝60°，AD＝80．ABCDαβ在Rt△ADB中，∵tanα＝，∴BD＝AD·tanα＝80×tan45°＝80．………2分在Rt△ADC中，∵tanβ＝，∴CD＝AD·tanβ＝80×tan60°＝80．……5分∴BC＝BD＋CD＝80＋80≈218.6．答：这栋楼高约为218.6m．………………7分18．(1)a＝25%，90º．2分补全条形图．4分(2)众数是5，中位数是5．8分(3)该市初一学生第一学期社会实践活动时间不少于5天的人数约是：20000×(30%＋25%＋20%)＝15000(人)．12分ABCDEO19．(1)证法一：连接AE，1分∵AC为⊙O的直径，∴∠AEC＝90º，即AE⊥BC．4分∵AB＝AC，∴BE＝CE，即点E为BC的中点．6分ABCDEO证法二：连接OE，1分∵OE＝OC，∴∠C＝∠OEC．∵AB＝AC，∴∠C＝∠B，∴∠B＝∠OEC， ∴OE∥AB．4分∴＝＝1，∴EC＝BE，即点E为BC的中点．6分(2)∵∠COD＝80º，∴∠DAC＝40º，8分∵∠DAC＋∠DEC＝180º，∠BED＋∠DEC＝180º，∴∠BED＝∠DAC＝40º．11分20．解：(1)设A型计算器进价是x元，B型计算器进价是y元，1分得：，3分解得：．5分答：每只A型计算器进价是40元，每只B型计算器进价是60元．6分(2)设购进A型计算器为z只，则购进B型计算器为(50－z)只，得：，9分解得：24≤z≤26，因为z是正整数，所以z＝24，25，26．11分答：该经销商有3种进货方案：①进24只A型计算器，26只B型计算器；②进25只A型计算器，25只B型计算器；③进26只A型计算器，24只B型计算器．12分21．解：(1)BE＝(t＋4)cm，1分AB(D)CEFEF＝(t＋4)cm．4分(2)分三种情况讨论：①当DF＝EF时，有∠EDF＝∠DEF＝∠B，ABCDEF∴点B与点D重合，∴t＝0．…5分②当DE＝EF时，∴4＝(t＋4)，ABCDEF解得：t＝．7分③当DE＝DF时，有∠DFE＝∠DEF＝∠B＝∠C，∴△DEF∽△ABC．ABCDEMPFN∴＝，即＝，解得：t＝．9分ABCQLKPRTS综上所述，当t＝0、或秒时，△DEF为等腰三角形．(3)设P是AC的中点，连接BP，∵EF∥AC，∴△FBE∽△ABC．∴＝，∴＝．又∠BEN＝∠C，∴△NBE∽△PBC，∴∠NBE＝∠PBC．10分∴点N沿直线BP运动，MN也随之平移．如图，设MN从ST位置运动到PQ位置，则四边形PQST是平行四边形．11分 ∵M、N分别是DF、EF的中点，∴MN∥DE，且ST＝MN＝DE＝2．分别过点T、P作TK⊥BC，垂足为K，PL⊥BC，垂足为L，延长ST交PL于点R，则四边形TKLR是矩形，当t＝0时，EF＝(0＋4)＝，TK＝EF·sin∠DEF＝××＝；当t＝12时，EF＝AC＝10，PL＝AC·sinC＝×10×＝3．∴PR＝PL－RL＝PL－TK＝3－＝．∴S□PQST＝ST·PR＝2×＝．∴整个运动过程中，MN所扫过的面积为cm2．13分…………………1分…………………2分22．解：(1)由题意得：，解得：．∴抛物线解析式为y＝x2－x＋4．3分ABCOxyQTC"(2)令y＝0，得：x2－x＋4＝0．解得：x1＝1，x2＝3．∴C点坐标为(1，0)．4分作CQ⊥AB，垂足为Q，延长CQ，使CQ＝C"Q，则点C"就是点C关于直线AB的对称点．由△ABC的面积得：CQ·AB＝CA·OB，∵AB＝＝5，CA＝2，∴CQ＝，CC"＝．6分作C"T⊥x轴，垂足为T，则△CTC"∽△BOA．∴＝＝，∴C"T＝，CT＝．∴OT＝1＋＝∴C"点的坐标为(，)8分(3)设⊙D的半径为r，∴AE＝r＋3，BF＝4－r，HB＝BF＝4－r．∵AB＝5，且AE＝AH，ABCOxyDEFHPN∴r＋3＝5＋4－r，∴r＝3．10分HB＝4－3＝1．作HN⊥y轴，垂足为N，则＝，＝，∴HN＝，BN＝，∴H点坐标为(－，)．12分根据抛物线的对称性，得PA＝PC，∵|PH－PA|＝|PH－PC|≤HC，∴当H、C、P三点共线时，|PH－PC|最大．∵HC＝＝， ∴|PH－PA|的最大值为．14分'