2014年泉州市初中学业质量检查数学试题含答案(word版)

'2014年福建省泉州市初中学业质量检查数学试卷（试卷满分:150分；考试时间:120分钟）友情提示：所有答案必须填写到答题卡相应的位置上．一、选择题（每小题3分，共21分）每小题有四个答案，其中有且只有一个答案是正确的，请在答题卡上相应题目的答题区域内作答，答对的得3分，答错或不答的一律得0分．1．计算：3×（-1）等于（）．A．B．C．D．2．计算：等于（）．A．B．　C．　D．3．如图，数轴上表示的是某不等式组的解集，则这个不等式组可以是（）．3210-1-2（第3题图）A．B．C．D．4．在某次体育测试中，九年级某班7位同学的立定跳远成绩（单位：m）分别为：2.15，2.25，2.25，2.31，2.42，2.50，2.51，则这组数据的中位数是（　　）．A．2.15B．2.25C．2.31D．2.425．若边形的内角和是，则的值是（　　）．A．B．C．D．6．如图是一个正方体被截去一角后得到的几何体，它的俯视图是（　　）．正面（第6题图）A．B．C．D．A（第7题图）BCDEF7．如图，在中,,D、E分别是AB、BC的中点,F在CA的延长线上，，AC=6，AB=8，则四边形AEDF的周长为（）．A．22　　Ｂ．20　Ｃ．18　Ｄ．16二、填空题（每小题4分，共40分）在答题卡上相应题目的答题区域内作答．8．-2的相反数是．9．分解因式：．10．世界文化遗产长城总长约为6700000m，将6700000用科学记数法表示为．11．计算：．12．方程的解是．13．在菱形ABCD中，AB=3cm，则菱形ABCD的周长为．14．已知扇形的圆心角为，弧长是cm，则扇形的半径是．15．如图，点C在直线MN上，于点C，°，则°．BACMN12（第15题图）（第16题图）AHPOxy（第17题图）ABCDP16．如图，点A在函数．（x>0）的图象上，过点A作轴，点P是x轴上的一个动点，连结PA、PH，则的面积为．17．如图，在边长为1的小正方形网格中，点A、B、C、D都在这些小正方形的顶点上，连结AB．（1）AB的长为；（2）连结CD与AB相交于点P，则的值是．三、解答题（共89分）在答题卡上相应题目的答题区域内作答．18．（9分）计算：．19．（9分）先化简，再求值：，其中．20．（9分）已知：如图，在中，AB=AC，D为BC的中点，过点D作DE⊥AB，DF⊥AC，垂足分别为E、F．求证：≌．ABCDEF（第20题图） 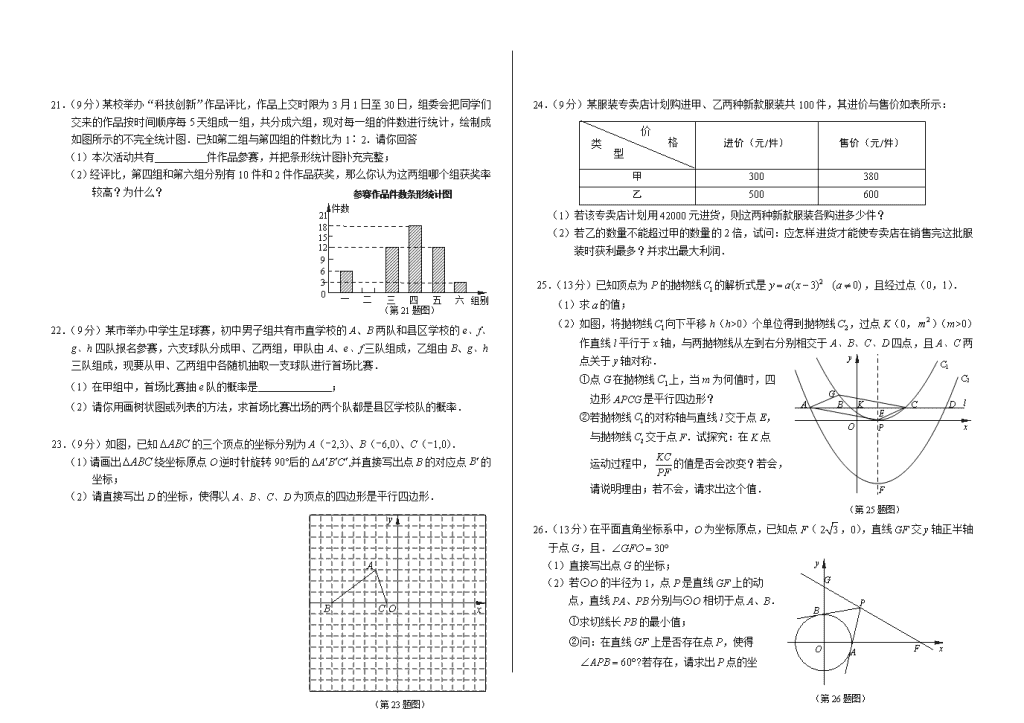21．（9分）某校举办“科技创新”作品评比，作品上交时限为3月1日至30日，组委会把同学们交来的作品按时间顺序每5天组成一组，共分成六组，现对每一组的件数进行统计，绘制成如图所示的不完全统计图．已知第二组与第四组的件数比为1∶2．请你回答（1）本次活动共有件作品参赛，并把条形统计图补充完整；组别36912151821一1六二三四五件数参赛作品件数条形统计图（第21题图）0（2）经评比，第四组和第六组分别有10件和2件作品获奖，那么你认为这两组哪个组获奖率较高？为什么？22．（9分）某市举办中学生足球赛，初中男子组共有市直学校的A、B两队和县区学校的e、f、g、h四队报名参赛，六支球队分成甲、乙两组，甲队由A、e、f三队组成，乙组由B、g、h三队组成，现要从甲、乙两组中各随机抽取一支球队进行首场比赛．（1）在甲组中，首场比赛抽e队的概率是；（2）请你用画树状图或列表的方法，求首场比赛出场的两个队都是县区学校队的概率．23．（9分）如图，已知的三个顶点的坐标分别为A（-2,3）、B（-6,0）、C（-1,0）．（1）请画出绕坐标原点O逆时针旋转90°后的,并直接写出点B的对应点的坐标；（2）请直接写出D的坐标，使得以A、B、C、D为顶点的四边形是平行四边形．Ay一yBBCOx（第23题图）24．（9分）某服装专卖店计划购进甲、乙两种新款服装共100件，其进价与售价如表所示：进价（元/件）售价（元/件）甲300380乙500600价格类型（1）若该专卖店计划用42000元进货，则这两种新款服装各购进多少件？（2）若乙的数量不能超过甲的数量的2倍，试问：应怎样进货才能使专卖店在销售完这批服装时获利最多？并求出最大利润．25．（13分）已知顶点为P的抛物线的解析式是，且经过点（0，1）．（1）求的值；（2）如图，将抛物线向下平移h（h>0）个单位得到抛物线，过点K（0，）（m>0）Ay一yBx（第25题图）OGPKCDBEFlC2C1作直线l平行于x轴，与两抛物线从左到右分别相交于A、B、C、D四点，且A、C两点关于y轴对称．①点G在抛物线上，当m为何值时，四边形APCG是平行四边形？②若抛物线的对称轴与直线l交于点E，与抛物线交于点F．试探究：在K点运动过程中，的值是否会改变？若会，请说明理由；若不会，请求出这个值．（第26题图）yBAFxOPG26．（13分）在平面直角坐标系中，O为坐标原点，已知点F（，0），直线GF交y轴正半轴于点G，且．（1）直接写出点G的坐标；（2）若⊙O的半径为1，点P是直线GF上的动点，直线PA、PB分别与⊙O相切于点A、B．①求切线长PB的最小值；②问：在直线GF上是否存在点P，使得?若存在，请求出P点的坐 标；若不存在，请说明理由．2014年福建省泉州市初中学业质量检查数学试题参考答案及评分标准说明：（一）考生的正确解法与“参考答案”不同时，可参照“参考答案及评分标准”的精神进行评分．（二）如解答的某一步出现错误，这一错误没有改变后续部分的考查目的，可酌情给分，但原则上不超过后面应得的分数的二分之一；如属严重的概念性错误，就不给分．（三）以下解答各行右端所注分数表示正确做完该步应得的累计分数．一、选择题（每小题3分，共21分）1．D　2．B　3．A　4．C　5．C　6．A7．D二、填空题（每小题4分，共40分）8．　9．　10．　11．　12．13．　14．15．　16．17．（1）；（2）2三、解答题（共89分）18.（本小题9分）解：原式……………………………………………………………8分………………………………………………………………………9分19．（本小题9分）解：原式…………………………………………………4分………………………………………………………………6分当时，原式………………………………………7分…………………………………………………9分20．（本小题9分）证明：∵,ABCDEF（第20题图）∴……………3分∵，∴.…………………6分∵为边的中点,∴,……8分∴≌.………………………9分组别36912151821一1六二三四五件数参赛作品件数条形统计图(第21题图)021．（本小题9分）解：（1）60，补图如右；（填空3分，补图2分，共5分）（2）由图可得：第四组的件数是18件，第六组的件数是3件，故第四组的获奖率为：，第六组的获奖率为：,……………………8分∵，∴第六组获奖率较高.…………………………………………………………………9分22．（本小题9分）解：（1）（e队出场）=;…………………………………………………………3分AefBghBghBgh甲组乙组（2）解法一:画树状图……………………6分由树状图可知，共有9种机会均等的情况，其中首场比赛出场的两个队都是县区学校队的有4种情况，（两队都是县区队）=.………………………………………9分解法二：列表甲组乙组…………………6分由树状图可知，共有9种机会均等的情况，其中首场比赛出场的两个队都是县区学校队的有4种情况，（两队都是县区队）=.………………………9分Ay一yBBCOx（第23题图）B′BB′BB′B23．（本小题9分）解：（1）如图所示：…………………………3分点的对应点的坐标为（0，-6）；……6分（2）第四个顶点D的坐标、、；……………………………………9分 24．（本小题9分）解：（1）设甲种新款服装购进件，那么乙种新款服装购进件，由题意可得，解得.………………………………2分经检验,符合题意.当时，(件).答：甲种新款服装购进40件，乙种新款服装购进60件.………………………………4分（2）解法一：设甲种新款服装购进件，那么乙种新款服装购进件，由题意可得,解得.…………………………………………………………………6分的取值范围为.同样售出一件新款服装,甲的获利比乙少,只能取,此时获利为（元）.答：甲种新款服装购进34件，乙种新款服装购进66件，才能使专卖店在销售完这批服装时获利最多,最大利润为元.…………………………………………………9分解法二：设该专卖店销售完这批服装可获利润元，甲种服装件.依题意可得，,整理得.∴是的一次函数，且.∴随的增大而减小.∵乙的数量不能超过甲的数量的倍，∴，解得,…………………………………………………………6分的取值范围为.∵为整数，∴时，取得最大值，此时（元）.答：该专卖店购进甲种服装34件，乙种服装66件，销售完这批服装时获利最多，此时利润为元．…………………………………………………………………………9分25．（本小题13分）解：（1）∵抛物线的过点，∴，解得：.∴设抛物线的解析式为.…………3分(2)①∵点、关于轴对称，∴点为的中点.若四边形是平行四边形，则必有点是的中点.Ay一yBx(第25题图)OGPKCDBEFlC2C1Q过点作轴于点，可得：≌，∴，，.∴点.……………………………5分∵顶点在抛物线上，∴，解得：，又，∴.∴当时，四边形是平行四边形.……………………………………8分②在抛物线中，令，解得：，又，且点在点的右侧，∴，.…………………………………………………9分∵点、关于轴对称， ∴.∵抛物线向下平移个单位得到抛物线，∴抛物线的解析式为：.∴，解得：，∴.∴……………………13分26．（本小题13分）yBAFxOPG(P1)P2(第26题图)H解：（1）点的坐标是；………………………3分（2）解法一：①连结、.∵切⊙于点，∴；根据勾股定理得：，∵不变，若要最小，则只须最小.即当时，线段最短，………………6分在中，,∴，∴==…………8分解法二：设直线解析式为.∵直线过点、,,∴解得：∴.……………………………………………………………………………5分设.过作轴于点,连结、,在中,.与⊙相切，,.在中,.∵均与⊙相切,∴.当，为最小，最小，此时.………………………8分②方法一：存在．∵均与⊙相切，∴平分.∵，∴.∵，∴.∴点是以点为圆心，为半径的圆与直线的交点，即图中的两点.∵，∴点与点重合.………………………………………………10分在中，，∴.∵，∴是等边三角形,∴.∵，∴，∴为的中点,∴.综上所述，满足条件的点坐标为或.……………………………………13分方法二：假设在直线上存在点，使得，则必须有. ,.，.……………………………………………………………………10分由①解法二可知，，解得，.满足条件的点坐标为或.…………………………………13分'