定稿2010年漳州一中高三毕业班质量检查数学试卷

'学校___________________班级_________________姓名_________________座号________________线封密2010年漳州一中高三毕业班质量检查数学科（文科）试卷第Ⅰ卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．设全集S={a，b，c，d，e}，集合A={a，c}，B={b，e}，则下面论断正确的是（）（A）A∪B=S（B）ACSB（C）CSAB（D）CSA∩CSB=2．已知向量=(2，1)，=(1，k)，若⊥，则实数k等于（）（A）（B）3（C）-7（D）-23．复数z1＝1＋bi，z2＝－2＋i，若的实部和虚部互为相反数，则实数b的值为（）（A）7（B）（C）（D）-74．某同学使用计算器求30个数据的平均数时，错将其中一个数据105输入为15，那么由此求出的平均数与实际平均数的差是()（A）3.5（B）-3（C）3（D）-0.55．已知，，则的图象（）（A）与的图象相同（B）向左平移个单位，得到的图象（C）与的图象关于y轴对称（D）向右平移个单位，得到的图象6.下面四个命题：　　①“直线a∥直线b”的充要条件是“a平行于b所在的平面”；②“直线l⊥平面内所有直线”的充要条件是“l⊥平面”；③“直线a、b为异面直线”的充分不必要条件是“直线a、b不相交”；④“平面∥平面”的必要不充分条件是“平面内存在不共线三点到平面的距离相等”．其中正确命题的序号是()数学（文科）试卷第5页（共4页） （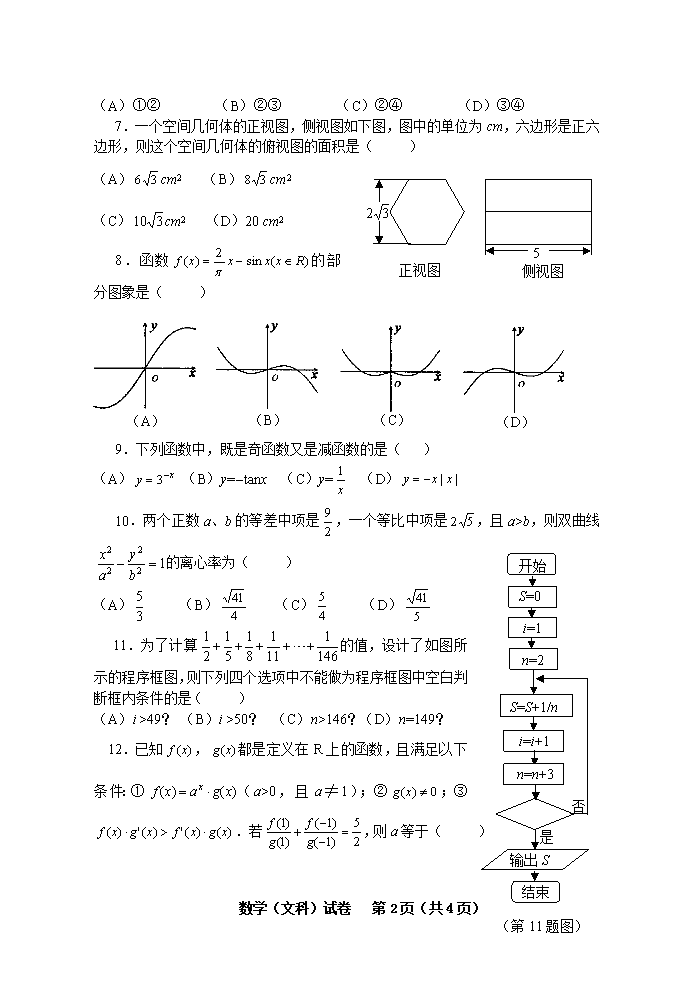A）①②（B）②③（C）②④（D）③④5正视图侧视图7．一个空间几何体的正视图，侧视图如下图，图中的单位为cm，六边形是正六边形，则这个空间几何体的俯视图的面积是（）（A）cm2（B）cm2（C）cm2（D）20cm2（A）（B）（C）（D）8．函数的部分图象是（）9．下列函数中，既是奇函数又是减函数的是（）（A）（B）y=-tanx（C）y=（D）开始S=0i=1S=S+1/n是i=i+1否输出S结束n=2n=n+3（第11题图）10．两个正数a、b的等差中项是，一个等比中项是，且a>b，则双曲线的离心率为（）（A）（B）（C）（D）11．为了计算的值，设计了如图所示的程序框图，则下列四个选项中不能做为程序框图中空白判断框内条件的是（）（A）i>49？（B）i>50？（C）n>146？（D）n=149？12．已知，都是定义在R上的函数，且满足以下条件：①（a>0，且a≠1）；②；③．若，则a等于（）数学（文科）试卷第5页（共4页） （A）（B）2（C）（D）2或第Ⅱ卷（非选择题共90分）二、填空题（本大题共4小题，每小题4分，共16分）13．在约束条件下，z=4-2x+y的最大值是______________．14．设等差数列的前项和为，若，则．15．过点M(1，2)的直线l与圆C：(x-3)2+(y-4)2=25交于A，B两点，C为圆心，当∠ACB最小时，直线l的方程是．16．有些计算机对表达式的运算处理过程实行“后缀表达式”：运算符号紧跟在运算对象的后面，按照从左到右的顺序运算，如表达式，其运算为：，若计算机进行运算：，那么使此表达式有意义的的范围为___________________________．三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）ABC17．（本小题满分12分）把一个棋子放在△ABC的顶点A，棋子每次跳动只能沿△ABC的一条边从一个顶点跳到另一个顶点，并规定：抛一枚硬币，若出现正面朝上，则棋子按逆时针方向从棋子所在的顶点跳到△ABC的另一个顶点；若出现反面朝上，则棋子按顺时针方向从棋子所在的顶点跳到△ABC的另一个顶点．现在抛3次硬币，棋子按上面的规则跳动3次．（Ⅰ）列出棋子从起始位置A开始3次跳动的所有路径（用△ABC顶点的字母表示）；（Ⅱ）求3次跳动后，棋子停在A点的概率．OCAB18．（本小题满分12分）如图，△OAB是等边三角形，∠AOC=，OC=，A、B、C三点共线，（Ⅰ）求sin∠BOC的值；（Ⅱ）求线段BC的长．数学（文科）试卷第5页（共4页） 19．（本小题满分12分）已知是等比数列｛｝的前n项和，，，．（Ⅰ）求和；（Ⅱ）设各位上的数字之和为，求数列｛｝的前n项和．ABCDP20．（本小题满分12分）如图，四棱锥P-ABCD中，PA=AB=AD=1．（Ⅰ）请你在下面四个选项中选择2个作为条件，使得能推出平面PCD⊥平面PAD，并证明．①PB=PD=；②四边形ABCD是正方形；③PA⊥平面ABCD；④平面PAB⊥平面ABCD．（Ⅱ）在（Ⅰ）选择的条件下，在四棱锥P-ABCD的表面上任取一个点，求这个点在四棱锥P-ABCD侧面内的概率．OxyABCMF21．（本题满分12分）已知椭圆，直线l与椭圆交于A、B两点，M是线段AB的中点，连接OM并延长交椭圆于点C．直线AB与直线OM的斜率分别为k、m，且．（Ⅰ）求的值；（Ⅱ）若直线AB经过椭圆的右焦点F，问：对于任意给定的不等于零的实数k，是否存在a∈[2，+∞)，使得四边形OACB是平行四边形，请证明你的结论．22．（本小题满分14分）已知函数．（Ⅰ）求函数的单调区间和极值；数学（文科）试卷第5页（共4页） （Ⅱ）设P(x1，y1)，Q(x2，y2)是函数图象上的两点且，，若直线PQ是函数图象的切线且P、Q都是切点，求证：；（参考数据：ln2≈0.6931，ln3≈1.0986）（Ⅲ）设函数g(x)的定义域为D，区间ID，若函数g(x)在I上可导，对任意的x0∈I，g(x)的图象在(x0，g(x0))处的切线为l，函数g(x)图象上所有的点都在直线l上方或直线l上，则称区间I为函数g(x)的“下线区间”．类比上面的定义，请你写出函数“上线区间”的定义，并根据你所给的定义，判断区间（-∞，）是否是函数的“上线区间”（不必证明）．数学（文科）试卷第5页（共4页）'