2012届广东省梅州市高三总复习质量检查数学文科试卷及答案

'试卷类型：B梅州市高三总复习质检试卷（2012.5）数学（文科）本试卷共4页，21小题，满分150分。考试用时120分钟。注意事项：1．答卷前，考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。将条形码横贴在答题卡右上角“条形码粘贴处”。2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。不按以上要求作答的答案无效。4．作答选做题时，请先用2B铅笔填涂选做题的题号对应的信息点，再作答。漏涂、错涂、多涂的，答案无效。5．考生必须保持答题卡的整洁。考试结束后，将试卷和答题卡一并交回。一、选择题：本大题共10个小题，每小题5分，满分50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．设，若复数，则在复平面上对应的点在A．第一象限B．第二象限C．第三象限D．第四象限2．已知集合，则集合等于A．B．C．D．3．设表示两条直线，表示两个平面，下列命题中的真命题是A．B．C．D．4．设，函数的图象向右平移个单位后与原图象重合，则的最小值为A．B．C．D．35．平面向量共线的充要条件是A．方向相同B．两向量中至少有一个为零向量C．D．存在不全为零的实数，6．以双曲线的左焦点为焦点，顶点在原点的抛物线方程是A．B．C．D． 7．函数的图象大致为A．B．C．D．8．在区间上随机取一个数的值介于于0到之间的概率为A．B．C．D．9．己知函数是上的偶函数，若对于，都有，且当时，，则的值为A．B．C．1D．210．设是一个至少含有两个数的数集，若对任意，都有（除数），则称是一个数域，例如有理数集是数域.有下列命题：①数域必含有0，1两个数；②整数集是数域；③若有理数集，则数集必为数域；④数域必为无限集．其中正确命题的个数是A．1个B．2个C．3个D．4个二、填空题：本大题共5小题，考生作答4小题，每小题5分，满分20分．（一）必做题（11~13小题）11．若，则的最小值为．12．执行如图所示的程序框图，若输入10，则输出的值为．13．设等差数列的前项和为，若，则．（二）选做题（14、15题，考生只能从中选做一题）T14．（坐标系与参数方程选做题）在极坐标系中，直线与圆的交点个数为．15．（几何证明选讲选做题）如图所示，过外一点作一条直线与交于两点，己知弦，点到的切线长则． 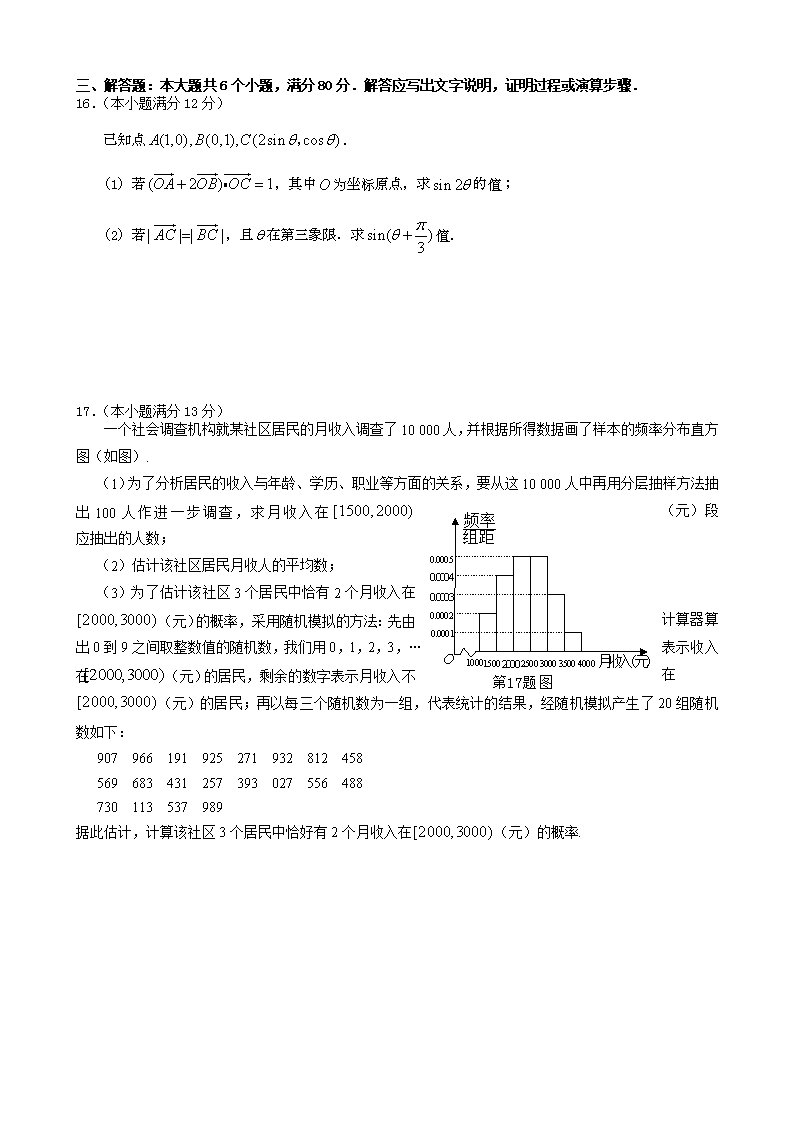三、解答题：本大题共6个小题，满分80分．解答应写出文字说明，证明过程或演算步骤．16．（本小题满分12分）己知点.（1）若，其中为坐标原点，求的值；（2）若，且在第三象限．求值.17．（本小题满分13分）一个社会调查机构就某社区居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图（如图）.（1）为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法抽出100人作进一步调查，求月收入在（元）段应抽出的人数；（2）估计该社区居民月收人的平均数；（3）为了估计该社区3个居民中恰有2个月收入在（元）的概率，采用随机模拟的方法：先由计算器算出0到9之间取整数值的随机数，我们用0，1，2，3，…表示收入在（元）的居民，剩余的数字表示月收入不在（元）的居民；再以每三个随机数为一组，代表统计的结果，经随机模拟产生了20组随机数如下：907966191925271932812458569683431257393027556488730113537989据此估计，计算该社区3个居民中恰好有2个月收入在（元）的概率. 18．（本小题满分14分）已知直三棱柱的三视图如图所示；(1)求此三棱柱的体积和表面积；(2)画出此三棱柱，并证明：19.（本小题14分）己知椭圆的离心率为，不等式所表示的平面区域的面积为.(1)求椭圆的方程；(2)设椭圆的左项点为，上顶点为，圆过两点．当圆心与原点的距离最小时，求圆的方程．20．（本小题14分）定义在上的函数满足：，且当时，.(1)求的值，并证明是定义域上的增函数：(2)数列满足，，求数列的通项公式及前项和.21．（本小题14分）已知函数.（1）当时，求的最大值；（2）试讨论函数的零点情况；（3）设均为正数，若，求证：． '