2010年福建省福州市高中毕业班质量检查理科数学试卷

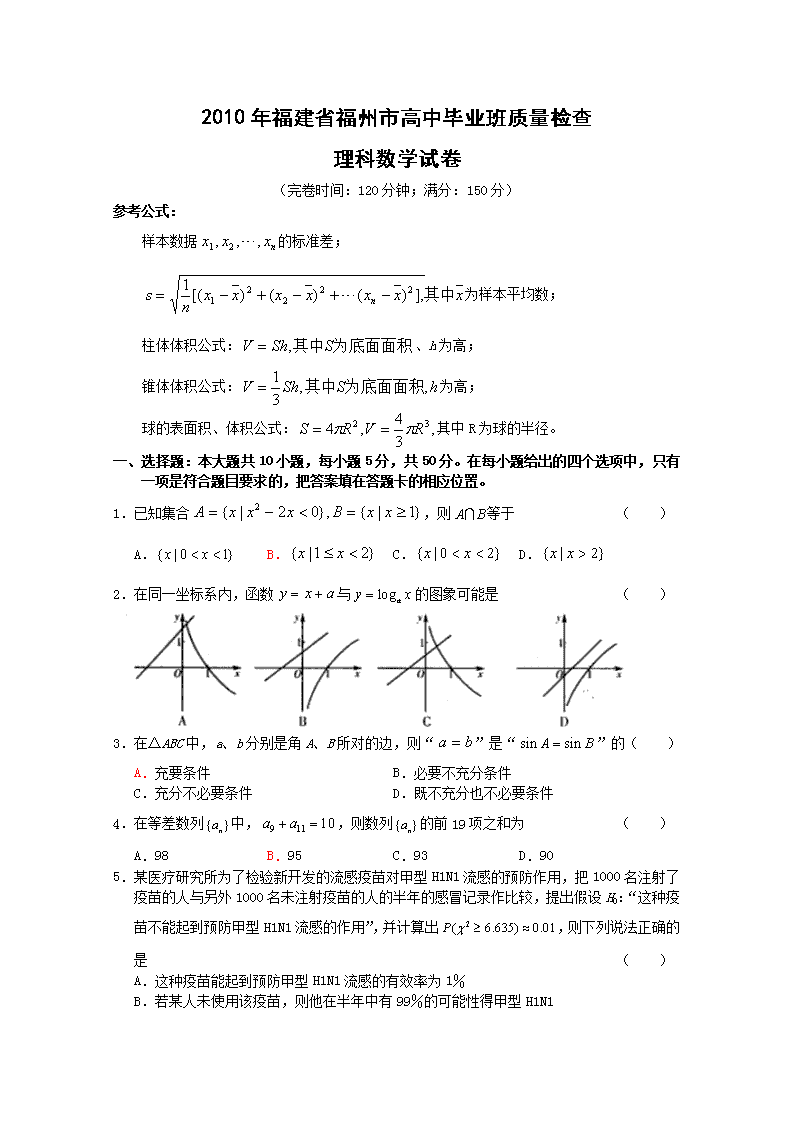
'2010年福建省福州市高中毕业班质量检查理科数学试卷（完卷时间：120分钟；满分：150分）参考公式：样本数据的标准差；为样本平均数；柱体体积公式：、h为高；锥体体积公式：为高；球的表面积、体积公式：其中R为球的半径。一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的，把答案填在答题卡的相应位置。1．已知集合，则等于（）A．B．C．D．2．在同一坐标系内，函数与的图象可能是（）3．在△ABC中，a、b分别是角A、B所对的边，则“”是“”的（）A．充要条件B．必要不充分条件C．充分不必要条件D．既不充分也不必要条件4．在等差数列中，，则数列的前19项之和为（）A．98B．95C．93D．905．某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用，把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录作比较，提出假设H0：“这种疫苗不能起到预防甲型H1N1流感的作用”，并计算出，则下列说法正确的是（）A．这种疫苗能起到预防甲型H1N1流感的有效率为1％B．若某人未使用该疫苗，则他在半年中有99％的可能性得甲型H1N1 C．有1％的把握认为“这种疫苗能起到预防甲型H1N1流感的作用”D．有99％的把握认为“这种疫苗能起到预防甲型H1N1流感的作用”6．设、是两个不同的平面，l、m是两条不重合的直线，下列命题中正确的是（）A．若，则B．若，则C．若，则D．若，则7．如图为互相垂直的单位向量，向量可表示为（）A．B．C．D．8．设的展开式的常数项是（）A．12B．6C．4D．29．已知函数的解，且的值（）A．恒为负B．等于零C．恒为正D．不小于零10．若直线没有公共点，则过点的一条直线与椭圆的公共点的个数是（）A．0B．1C．2D．1或2二、填空题：本大题共5小题，每小题4分，共20分。把答案填在答题卡的相应位置。11．如右图，一个空间几何体的正视图和侧视图都是边长为2的正三角形，俯视图是一个圆，那么该几何体的体积是。12．已知i是虚数单位，使为实数的最小正整数n是。13．农科院小李在做某项实验中，计划从花生、大白菜、土豆、玉米、小麦、苹果这6种种子中选出4种，分别种植在四块不同的空地上（一块空地只能种一种作物），若小李已决定在第一块空地上种玉米或苹果，则不同的种植方案有种（用数字作答）。 14．某程序流程框图如图所示，现执行该程序，输入下列函数，则可以输出的函数是=。15．函数的定义域为D，若对于任意，当时，都有，则称函数在D上为非减函数。设函数在[0，1]上为非减函数，且满足以下三个条件：①；②；③则的值为。三、解答题：本大题共6小题，共80分。解答写在答题卡相应位置，应写出文字说明、证明过程或演算步骤16．（本小题满分13分）数列上，（I）求数列的通项公式；（II）若17．（本小题满分13分）从某自动包装机包袋的食盐中，随机抽取20袋作为样本，按各袋的质量（单位：g）分成四组， ，相应的样本频率分布直方图如图所示。（I）估计样本中的位数是多少？落入的频数是多少？（II）现从这台自动包装机包袋的大批量食盐中，随机抽取3袋，记表示食盐质量属于的袋数，依样本估计总体的统计思想，求的分布列及期望18．（本小题满分13分）已知三棱柱ABC－A1B1C1的侧棱垂直于底面，，分别是的中点．（Ⅰ）证明：平面；（II）求二面角M—AN—B的余弦值。19．（本小题满分13分）如图，以原点O为顶点，以y轴为对称轴的抛物线E的焦点为F（0，1），点M是直线上任意一点，过点M引抛物线E的两条切线分别交x轴于点S，T，切点分别为B，A。（I）求抛物线E的方程；（II）求证：点S，T在以FM为直径的圆上；（III）当点M在直线l上移动时，直线AB恒过焦点F，求m的值。 20．（本小题满分14分）已知函数（I）求的最小值；（II）讨论关于x的方程的解的个数；（III）当21．（本小题满分14分）本题（1）、（2）、（3）三个选答题，每小题7分，任选2题作答，满分14分，如果多做，则按所做的前两题计分。作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中。（I）（本小题满分7分）选修4—2：矩阵与变换已知矩阵经矩阵A所对应的变换得直线l2，直线l2又经矩阵B所对应的变换得到直线，求直线l2的方程。（II）（本小题满分7分）选修4—4：坐标系与参数方程求直线截得的弦长。 （III）（本小题满分7分）选修4—5：不等式选讲若存在实数x满足不等式，求实数a的取值范围。 参考答案一、选择题：本大题共10小题，每小题5分，共50分。1—5BCABD6—10DCBAC二、填空题：本大题共5小题，每小题4分，共20分。11．12．413．12014．15．1三、解答题：本大题共6小题，共80分。16．（本小题满分13分）解：（I）上。………………2分是以3为首项，以2为公差的等差数，………………3分………………5分（II）①…………6分②…………7分由①—②得………………9分………………12分………………13分17．（本小题满分13分） 解：（I）由已知可得直线，把频率分布直方图分为左右两侧等面积，故估计样本的中位数是502.5（直接写出答案不扣分）…………2分样本落入………………4分故落入………………6分另解：样本落入………………4分故样本落入所以样本落入………………6分（II）依样本的频率代替概率，可得………………8分故的分布列为0123P0.0270.1890.4410.343………………11分从而或………………13分18．（本小题满分13分）解法一：依条件可知AB、AC，AA1两两垂直，如图，以点A为原点建立空间直角坐标系根据条件容易求出如下各点坐标： （I）证明：是平面ACCA1的一个法向量，且所以………………4分又，………………6分（II）设是平面AMN的法向量，因为，由………………8分得解得平面AMN的一个法向量………………10分由已知，平面ABC的一个法向量为………………11分………………12分………………13分解法二：（I）证明：设AC的中点为D，连结DN，A1D∵D，N分别是AC，BC的中点，∴………………1分 ∴A1D//MN………………4分………………6分（II）如图，设AB的中点为H，连结MH，∴MH//BB1∵BB1⊥底面ABC，∵BB1⊥AC，BB1⊥AB，∴MH⊥AC，AH⊥AB∴AB∩AC=A∴MH⊥底面ABC………………7分在平面ABC内，过点H做HG⊥AN，垂足为G连结MG，AN⊥HG，AN⊥MH，HG∩MH=H∴AN⊥平面MHG，则AN⊥MG∴∠MGH是二面角M—AN—B的平面角………………9分∵MH=BB1=2，由△AGH∽△BAC，得所以所以………………13分19．（本小题满分13分）解：（I）设抛物线E的方程为，依题意，所以抛物线E的方程为…………3分（II）设点，否则切线不过点M ………………5分………………7分∴AM⊥FT，即点T在以FM为直径的圆上；同理可证点S在以FM为直径的圆上，所以S，T在以FM为直径的圆上。………………8分（III）抛物线由则………………10分由（II）切线AM的方程为，同理消去………………12分………………13分20．（本小题满分14分）解：（I）………………1分的变化的情况如下： —0+极小值………………3分所以，………………4分（II）当单调递减且的取值范围是；当单调递增且下面讨论的解；所以，当时，原方程无解；………………6分当时，原方程有唯一解；当时，原方程有两解………………8分（III）原不等式可化为：令………………10分上单调递减，在上单调递增，………………12分 令…………14分21．（本小题满分14分）本题（1）、（2）、（3）三个选答题，每小题7分，任选2题作答，满分14分，如果多做，则按所做的前两题计分。作答时，先用2B铅笔在答题卡上把所选题目对应的题号涂黑，并将所选题号填入括号中。（1）（本小题满分7分）解：，，………………2分则有………………4分此时，同理可得即………………7分（2）（本小题满分7分）解：直线………………2分曲线半径为4的圆………………4分则圆心（1，—1）到直线…………5分设直线被曲线截得的弦长为t，则，∴直线被曲线截得的弦长为………………7分（3）（本小题满分7分）解法一：令则有，………………2分 由图象可得………………4分又因为原不等式有实数解，所以a的取值范围是………………7分解法二：的几何意义是x在数轴上对应点P到3、4对应的点A、B的距离之和|PA|+|PB|，………………2分通过讨论三种情况的点P位置，可得|PA|+|PB|的最小值为1，………………4分又因为原不等式有实数解，所以a的取值范围是………………7分解法三：………………2分的最小值为1………………4分又因为原不等式有实数解，所以a的取值范围是………………7分'