2010年莆田市初中毕业班质量检查数学试卷及答案

'2010年莆田市初中毕业班质量检查试卷数学（满分：150分；考试时间：120分钟）友情提醒：本试卷分为“试题”和“答题卡”两部分，答题时，请按答题卡中的“注意事项”认真作答，答案写在答题卡上的相应位置。一、精心选一选：本大题共8小题，每小题4分，共32分，每小题给出的四个选项中有且只有一个选项是正确的，请把正确选项的代号写在题后的括号内，答对的得4分；答错、不答或答案超过一个的一律得0分.1．下列运算正确的是（　　）A．B．C．D．2．方程的解是（）A．B．C．或D．或3．某鞋店试销一种新款女鞋，销售情况如下表所示：型号2222.52323.52424.525数量（双）351015832鞋店经理最关心的是，哪种型号的鞋销量最大．对他来说，下列统计量中最重要的是（）A．平均数B．众数C．中位数D．方差4．如图，把直线L沿x轴正方向向右平移2个单位得到直线L′，则直线L/的解析式为（）A.B.C.D.5．下列说法正确的是（）A．有两个角为直角的四边形是矩形B．矩形的对角线互相垂直C．等腰梯形的对角线相等（第4题图）D．对角线互相垂直的四边形是菱形6．如图，为一个圆锥的三视图，则此圆锥的侧面积是（）11 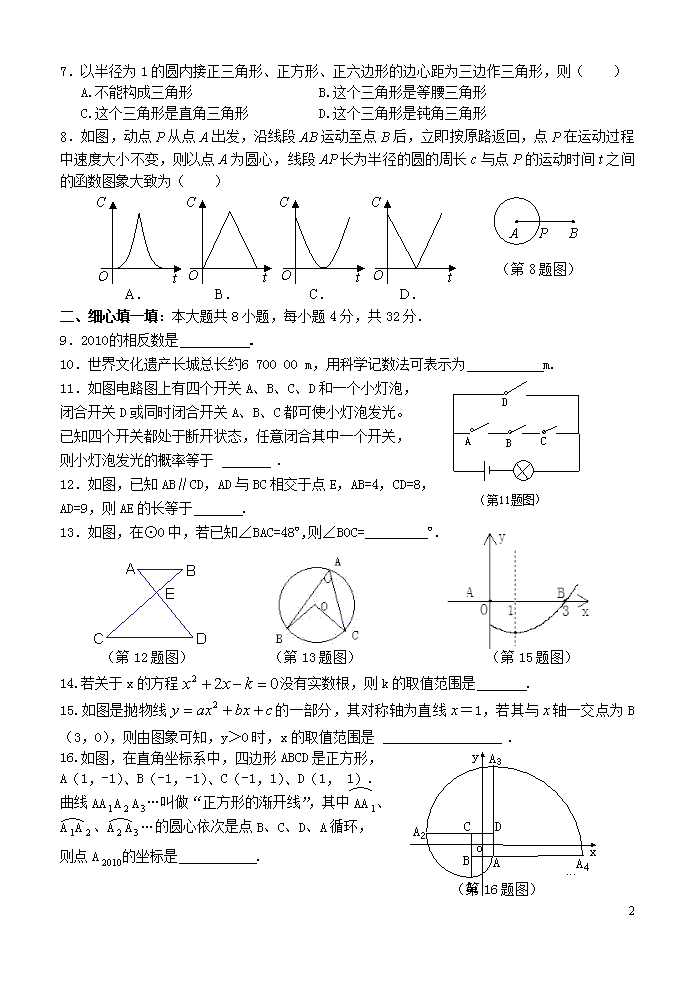7．以半径为1的圆内接正三角形、正方形、正六边形的边心距为三边作三角形，则（）A.不能构成三角形B.这个三角形是等腰三角形C.这个三角形是直角三角形D.这个三角形是钝角三角形8．如图，动点P从点A出发，沿线段AB运动至点B后，立即按原路返回，点P在运动过程中速度大小不变，则以点A为圆心，线段AP长为半径的圆的周长c与点P的运动时间t之间的函数图象大致为（）OCtOCtOCtOCtAPBA．B．C．D．（第8题图）二、细心填一填：本大题共8小题，每小题4分，共32分.9．2010的相反数是.10．世界文化遗产长城总长约670000m，用科学记数法可表示为m.11．如图电路图上有四个开关A、B、C、D和一个小灯泡，闭合开关D或同时闭合开关A、B、C都可使小灯泡发光。已知四个开关都处于断开状态，任意闭合其中一个开关，则小灯泡发光的概率等于.12．如图，已知AB∥CD，AD与BC相交于点E，AB=4，CD=8，AD=9，则AE的长等于.13．如图，在⊙O中，若已知∠BAC=48º,则∠BOC=_________º.（第12题图）（第13题图）（第15题图）14.若关于x的方程没有实数根，则k的取值范围是.15.如图是抛物线的一部分，其对称轴为直线＝1，若其与轴一交点为B（3，0），则由图象可知，y＞0时，x的取值范围是.16.如图，在直角坐标系中，四边形ABCD是正方形，A（1，-1）、B（-1，-1）、C（-1，1）、D（1，1）.曲线AAAA…叫做“正方形的渐开线”，其中AA、AA、AA…的圆心依次是点B、C、D、A循环，则点A的坐标是.（第16题图）11 三．耐心做一做：本大题共9小题，共86分，解答应写出必要的文字说明、证明过程或演算步骤17.（本小题满分8分）已知，求的值.18．（本小题满分8分）解不等式，并把解集在数轴上表示出来。ODCABEF19．（本小题满分8分）如图，线段与相交于点，E、F分别为OB、OC的中点，连接AB、DC、EF分别将“”记为①，“”记为②，“”记为③，要求同学从这三个等式中选出两个作为条件，一个作为结论.(在横线上填上序号)（第19题图）(1)写出一个真命题:如果、，那么.并证明这个真命题．(2)写出一个假命题：如果、，那么.20.（本小题满分8分）为了提高农民抵御大病风险的能力，全国农村推行了新型农村合作医疗政策，农民只需每人每年交10钱，就可以加入合作医疗，若农民患病住院治疗，出院后可到新型农村合作医疗办公室按一定比例报销医疗费.小军与同学随机调查了他们镇的一些村民，根据收集的数据制成如图所示的统计图。根据以上信息，解答下列问题：（1）本次共调查多少村民？有多少人参加合作医疗并的到报销款？（2）若该镇有村民10000人，请你估计大约有多少人参加了合作医疗保险？要使两年后参加合作医疗保险的人数达到9680人，假设这两年的增长率相同，求这个年增长率.11 21．（本小题满分8分）（1）如图1，D是△ABC的边BC上的一点，且,若△ABD的面积为,△ABC的面积为S，则:S=；（2）利用图1的结论在图2、3中将△ABC分别按以下两种方式分为三个面积相等的三角形，并说明分点所在的位置.22．（本小题满分10分）如图，以菱形ABCD的边AB为直径的⊙O交对角线AC于点P，过P作PE⊥BC，垂足为E。⑴求证：PE是⊙O的切线。⑵若菱形ABCD的面积为24，tan,求PE的长.23．（本小题满分10分）某水产品养殖企业为指导该企业某种水产品的养殖和销售，对历年市场行情和水产品养殖情况进行了调查．调查发现这种水产品的每千克售价y（元）与销售月份x（月）满足关系式，而其每千克成本y（元）与销售月份x（月）满足的函数关系，其图象如图所示．（1）求y的解析式；（2）问这种水产品下半年几月份出售每千克的利润最大？最大利润是多少？11 24．（本小题满分12分）某课题组在探究“泵站问题”时抽象出数学模型：直线l同旁有两个定点A、B，在直线l上存在点P，使得PA+PB的值最小.解法：作点A关于直线l的对称点A，连接AB，则AB与直线l的交点即为P，且PA+PB的最小值为AB.请利用上述模型解决下列问题：（1）几何应用：如图1，等腰直角三角形ABC的直角边长为2，E是斜边AB的中点，P是AC边上的一动点，则PB+PE的最小值为；（2）几何拓展：如图2,△ABC中，AB=2，∠BAC=30,若在AC、AB上各取一点M、N使BM+MN的值最小，求这个最小值；（3）代数应用：求代数式（0≤x≤4）的最小值.25．如图，矩形ABCD(点A在第一象限)与x轴的正半轴相交于M,，与y的负半轴相交于N，AB∥x轴，反比例函数y=的图象过A、C两点，直线AC与x轴相交于点E、与y轴相交于点F。(1)若B（-3，3），直线AC的解析式为y=.①求a的值；②连结OA、OC，若△OAC的面积记为S，△ABC的面积记为S，记S=S－S，问S是否存在最小值？若存在，求出其最小值；若不存在，请说明理由(2)AE与CF是否相等？请证明你的结论。11 （第25题图）2010年莆田市初中毕业班数学质量检查试卷参考答案一、精心选一选：1.D2.D3.B4.C5.C6.B7.C8.B二、细心填一填：9.-201010.6.711.12.313.14.k<-115.x<-1或x>316．（-4021，1）三．耐心做一做：17.解：∵2sin60∴(a+1)(a-1)=a=218.解：原不等式可化为2（2x-1）-3(5x+1)≤64x-2-15x-3≤6-11x≤11x≥-119.（1）①②→③或①③→②证明：∵∠OEF=∠OFE证明：∵∠A=∠D，AB=DC，∠AOB=∠DOC∴OE=OF∴△OAB≌△ODC∵E、F分别为OB、OC的中点∴OB=OC∴OB=OC∵E、F分别为OB、OC的中点在△OAB与△ODC中∴OE=OF∵∠A=∠D，∠AOB=∠DOC，OB=OC∴∠OEF=∠OFE∴△OAB≌△ODC∴AB=DC（2）②③→①20.答:（1）本次共调查500名村民被调查的村民中有400×5%=20人参加合作医疗并的到报销款（2）10000×（人）设这个增长率为x。依题意得解得：，（不合题意舍去）答：该镇大约有8000人参加了合作医疗保险,这个年增长率为10%。21.（1）:S=（2）11 22.（1）证明：连接OP、BP.∵四边形ABCD是菱形∴AB=BC∵AB是直径∴∠APB=90∴AP=PC又∵AO=OB∴OP∥BC∵PE⊥BC∴PE⊥OP所以PE是⊙O的切线.(2)∵=∴设PB=3x,则PA=4xS∴x=1PA=PC=4，PB=3∴AB=BC=5在Rt△BPC中，23.解(1)依题意得：解得（2）设这种水产品每千克的利润为y，则∵当x>4时，y随着X的增大而减小。x的取值范围是：7≤x≤12的整数∴当x=7时，即下半年7月份出售每千克的利润最大，最大利润是。24．（1）解：作点B关于AC的对称点B，连接BE交AC于P，此时PB+PE的值最小.连接AB.11 AB=AB=AE=∵∠BAC=∠BAC=45∴∠BAB=90∴PB+PE的最小值=BE=（2）作点B关于AC的对称点B，过B作BN⊥AB于N，交AC于M.此时BM+MN的值最小.BM+MN=BN.理由：如图1，在AC上任取一点M（不与点M重合），在AB上任取一点N，连接BM、BM、MN、BN.∵点B与点B关于AC对称∴BM=BM∴BM+MN=BM+MN>BN又∵BN>BN，BM+MN=BN∴BM+MN>BM+MN计算：如图2∵点B与点B关于AC对称∴AB=AB又∵∠BAC=30∴∠BAB=60图2∴△BAB是等边三角形∴BB=AB=2，∠BBN=60又∵BN⊥AB∴BN=BB=（3）方法一：构造图形如图所示其中：AB=4，AC=1，DB=2，AC=x，CA⊥AB于A，DB⊥AB于B.那么PC+PD=所求的最小值就是求PC+PD的最小值.作点C关于AB的对称点C，过C作CE垂直DB的延长线于E。则CE=AB=4，DE=2+1=3，CD=11 所求的最小值是5.方法二：构造图形如图所示在直角坐标系中，点A(0,1)、B(4,2)、P(x，0)（0≤x≤4）那么PA+PB=所求的最小值就是求PA+PB的最小值.作点C关于x轴的对称点A，过A作AC垂直于y轴，过点B作BC垂直于x轴交AC于点C。则AC=4，BC=3，AB=所求的最小值是5.25．解：（1）①方法一：∵四边形ABCD是矩形，AB∥x轴，B（-3，3）∴A（C（）∵y=经过A、C两点∴∴∵∴∴方法二：∵四边形ABCD是矩形，AB∥x轴，B（-3，3）∴A（C（）D(∴AB=，AD=∴AB=AD四边形ABCD是正方形，∴∠AEO=∠ACD=45∴OE=OF=bE(-b，0)∴∵∴②∵S=S=S11 ∴S=∴当k>时，S随着k的增大而增大.又∵k>0，k没有最小值，∴S没有最小值.（2）答：AE=CF，理由如下：方法一：连接MN，设AB交y轴于P点，BC角x轴于Q点.∵S∴∴又∵∠D=∠D∴△DNM∽△DCA∴∠DNM=∠DCA∴AF=MN∴MN∥AC同理CE=MN又∵AD∥y轴∴AF=CE∴四边形AFNM是平行四边形∴AE=CF方法二：设A(、C则AM=，AD=，CN=-，CD=∵EM∥CD又∵FN∥AD∴△AEM∽△ACD∴△CFN∽△CAD∴∴∴∴∴AE=CF方法三：设A(、C则M（m，0）、N(0，).则∴∴直线AC为：∴E(m+n,0)∴EM=∵CN=-∴EM=CN∵EM∥BA∥CN11 ∴∠AEM=∠FCN又∵∠AME=∠FNC=90∴△AEM≌△FCN∴AE=CF11'