第31届全国中学生物理竞赛决赛理论试题word

第31届全国中学生物理竞赛决赛理论考试试题一、（12分）一转速测量和控制装置的原理如图所示．在O点有电量为Q的正电荷，内壁光滑的轻质绝缘细管可绕通过O点的竖直轴在水平面内转动，在管内距离O为L处有一光电触发控制开关A，在O端固定有一自由长度为L／4的轻质绝缘弹簧，弹簧另一端与一质量为m、带有正电荷q`的小球相连接．开始时，系统处于静态平衡．细管在外力矩作用下，作定轴转动，小球可在细管内运动．当细管转速ω逐渐变大时，小球到达细管的A处刚好相对于细管径向平衡，并触发控制开关，外力矩瞬时变为零，从而限制转速过大；同时O点的电荷变为等量负电荷-Q．通过测量此后小球相对于细管径向平衡点的位置B，可测定转速．若测得OB的距离为L/2，求(1)弹簧系数k0及小球在B处时细管的转速；(2)试问小球在平衡点B附近是否存在相对于细管的径向微振动？如果存在，求出该微振动的周期．二、（14分）多弹头攻击系统是破解导弹防御体系的有效手段，如图所示，假设沿某海岸有两个军事目标W和N，两者相距L，一艘潜艇沿乎行于该海岸线的航线游弋，并监视这两个目标，其航线离海岸线的距离为d．潜艇接到攻击命令后浮出海面发射一颗可分裂成多弹头的母弹，发射速度为vo（其大小远大于潜艇在海里游弋速度的大小），假设母弹到达最高点时分裂成三个分弹头，每个分弹头的质量相等，分离时相对原母弹的速度大小均为v，且分布在同一水平面内，分弹头1、2为实弹，分弹头3为迷惑对方雷达探测的假弹头．如果两个实弹能够分别击中军事目标W和N，试求潜艇发射母弹时的位置与发射方向，并给出相应的实现条件．三、（14分)如图所示，某绝热容器被二块装有阀门K1和K2的固定绝热隔板分隔成相等体积Vo的三室A、B、C，VA=VB=VC=VO．容器左端用绝热活塞H封闭，左侧A室装有v1=1摩尔单原子分子气体，处在压强为P0、温度为To的平衡态；中段B室为真空；右侧c室装有V25 =2摩尔双原子分子气体，测得其平衡态温度为Tc＝0.50To．初始时刻K1和K2都处在关闭状态．然后系统依次经历如下与外界无热量交换的热力学过程：(1)打开K1，让vA中的气体自由膨胀到中段真空VB中；等待气体达到平衡态时，缓慢推动活塞H压缩气体，使得A室体积减小了30%（=0.70Vo）．求压缩过程前后，该部分气体的平衡态温度及压强；(2)保持K1开放，打开K2，让容器中的两种气体自由混合后共同达到平衡态．求此时混合气体的温度和压强；(3)保持K1和K2同时处在开放状态，缓慢拉动活塞H，使得A室体积恢复到初始体积=Vo．求此时混合气体的温度和压强．提示：上述所有过程中，气体均可视为理想气体，计算结果可含数值的指数式或分式；根据热力学第二定律，当一种理想气体构成的热力学系统从初态（Pi，Ti，Vi）经过一个绝热可逆过程（准静态绝热过程）到达终态(pf，Tf，Vf)时，其状态参数满足方程：其中，vI为该气体的摩尔数，Cv1为它的定容摩尔热容量，R为普适气体常量．而当热力学系统由二种理想气体组成，则方程(I)需修改为四、（20分）光纤光栅是一种介质折射率周期性变化的光学器件．设一光纤光栅的纤芯基体材料折射率为n1=1.51；在光纤中周期性地改变纤芯材料的折射率，其改变了的部分的材料折射率为n2=1.55；折射率分别为，n2和n1、厚度分别为d2和d1的介质层相间排布，总层数为N，其纵向剖面图如图(a所示．在该器件设计过程中，一般只考虑每层界面的单次反射，忽略光在介质传播过程中的吸收损耗，假设入射光在真空中的波长为λ=1.06μm，当反射光相干叠加加强时，则每层的厚度d1和d2最小应分别为多少？若要求器件反射率达到8%，则总层数N至少为多少？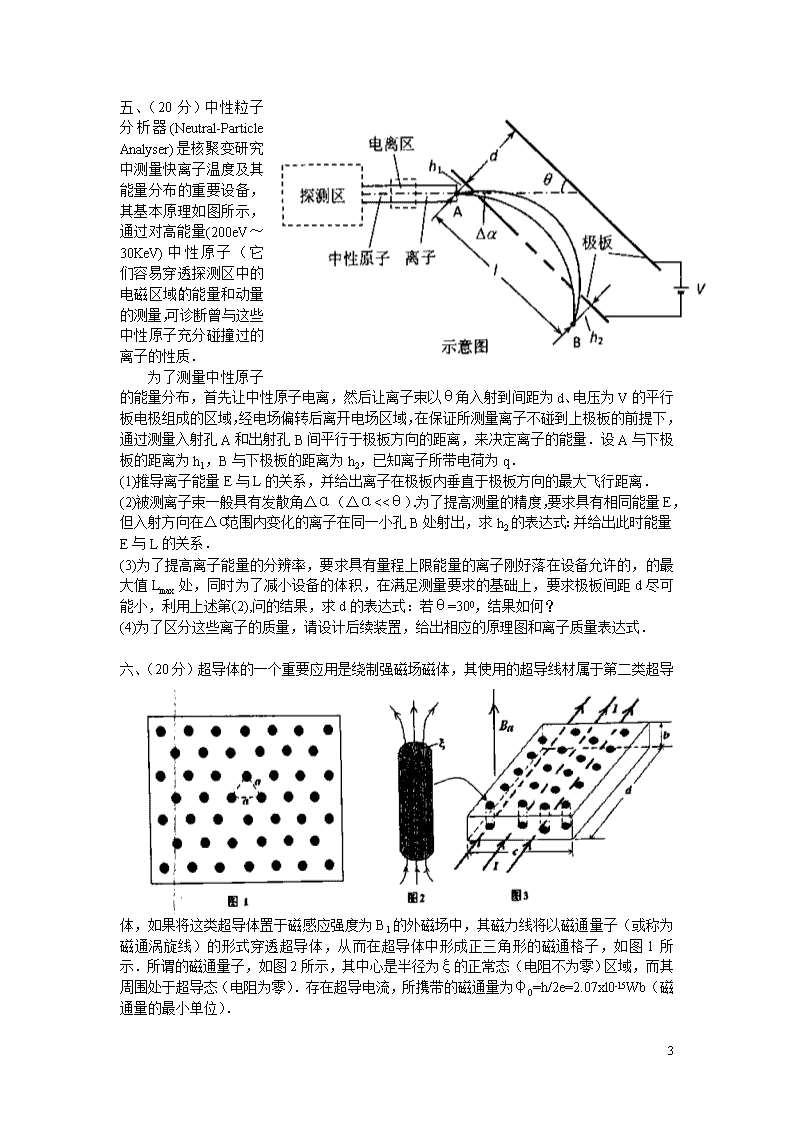提示：如图(b)所示，当光从折射率n1介质垂直入射到折射率n2介质时，界面上产生反射和透射，有：5 五、（20分）中性粒子分析器(Neutral-ParticleAnalyser)是核聚变研究中测量快离子温度及其能量分布的重要设备，其基本原理如图所示，通过对高能量(200eV～30KeV)中性原子（它们容易穿透探测区中的电磁区域）的能量和动量的测量，可诊断曾与这些中性原子充分碰撞过的离子的性质．为了测量中性原子的能量分布，首先让中性原子电离，然后让离子束以θ角入射到间距为d、电压为V的平行板电极组成的区域，经电场偏转后离开电场区域，在保证所测量离子不碰到上极板的前提下，通过测量入射孔A和出射孔B间平行于极板方向的距离，来决定离子的能量．设A与下极板的距离为h1，B与下极板的距离为h2，已知离子所带电荷为q．(1)推导离子能量E与L的关系，并给出离子在极板内垂直于极板方向的最大飞行距离．(2)被测离子束一般具有发散角Δα（△α<<θ）．为了提高测量的精度，要求具有相同能量E，但入射方向在△α范围内变化的离子在同一小孔B处射出，求h2的表达式：并给出此时能量E与L的关系．(3)为了提高离子能量的分辨率，要求具有量程上限能量的离子刚好落在设备允许的，的最大值Lmax处，同时为了减小设备的体积，在满足测量要求的基础上，要求极板间距d尽可能小，利用上述第(2),问的结果，求d的表达式：若θ=300，结果如何？(4)为了区分这些离子的质量，请设计后续装置，给出相应的原理图和离子质量表达式．六、（20分）超导体的一个重要应用是绕制强磁场磁体，其使用的超导线材属于第二类超导体，如果将这类超导体置于磁感应强度为B1的外磁场中，其磁力线将以磁通量子（或称为磁通涡旋线）的形式穿透超导体，从而在超导体中形成正三角形的磁通格子，如图1所示．所谓的磁通量子，如图2所示，其中心是半径为ξ的正常态（电阻不为零）区域，而其周围处于超导态（电阻为零）．存在超导电流，所携带的磁通量为φ0=h/2e=2.07xl0-l5Wb（磁通量的最小单位）．5 (1)若Ba=5xl0-2T，求此时磁通涡旋线之间距离a：(2)随着Ba的增大，磁通涡旋线密度不断增加．当Ba达到莱一临界值BC2时，整块超导体都变为正常态，假设磁通涡旋线芯的半径为ξ＝5xl0－9m．求所肘应的临界磁场BC2；(3)对于理想的第二类超导体，当有电流I通过超导带材时，在安培力的驱动下，磁通涡旋线将会粘滞流动，在超导惜内产生电阻（也称为磁通流阻）．从而产生焦耳损耗，不利于超导磁体的运行，磁通涡旋线稳定粘滞流动的速度v与单位体积磁通涡旋线所受到的驱动力fA和Ba的关系为fA=ηBav/φ0其中η为比例系数．外加磁场、电流方向，以及超导带材的尺寸如图3所示，请指出磁通涡旋线流动的方向，并求出磁通涡旋线流动所产生的电阻率（用Ba，φ0，η,导体尺寸b,c．d表示）(4)要使越导材料真正实用化，消除这种磁通流阻成了技术的关键，请给出你的解决方案．七、(20分)如图，两个质量均为m的小球A和B（均可视为质点），固定在中心位于C、长为2L的刚性轻质细杆的两端，构成一质点系，在竖直面内建立Oxy坐标，Ox方向沿水平向右，Oy方向竖直向上，初始时质点系中心C位于原点O，并以初速度vo竖直上抛，上抛过程中，ACB三点连线始终水平，风速大小恒定为u、方向沿x轴正向，小球在运动中所受空气阻力f的大小与相对于空气运动速度v的大小成正比，方向相反，即f=-kv，k为正的常量，当C点升至最高点时，恰好有一沿y轴正向运动、质量为m1、速度大小为ul的小石块（视为质点）与小球A发生竖直方向的碰撞，设碰撞是完全弹性的，时间极短，此后C点回落到上抛开始时的同一水平高度，此时它在Ox方向上的位置记为s，将从上抛到落回的整个过程所用时间记为T,质点系旋转的圈数记为n．求质点系(1)转动的初始角速度ω0，以及回落到s点时角速度ωs与n的关系：(2)从开始上抛到落回到s点为止的过程中，空气阻力做的功wf与n、s、T的关系．八、(20分)太阳是我们赖以生存的恒星，它的主要成分是氢元素，在自身引力的作用下收缩而导致升温，当温度高到一定程度时，中性原子将电离成质子和电子组成的等离子体，并在其核心区域达到约1.5xl07K的高温和l.6×l05kg/m3以上的高密度，产生热核聚变而放出巨大能量，从而抗衡自身的引力收缩达到平衡，而成为恒星．太阳内部主要核反应过程为其中第一个反应的概率由弱相互作用主导，概率很低，这恰好可以使得能量缓慢释放．反应产物正电子e+与电子e一湮灭为．γ射线，即已知：质子(lH)、氘(D)、氮－3(3He)、氮－4(4He)和电子的质量分别为938.27、1875.6l、2808.38、3727.36和0.5l（Mev/c2）（误差为0.01MeV／c2），c为真空中的光速，中微子νe的质量小于3ev／c2．普朗克常量h=6.626×10-34J．s，c=3.0×108m/s，波尔兹曼常量k=1.38l×10-23J/k．电子电量e=1.602×10一l9C．5 (1)试用理想气体模型估算处于热平衡状态的各种粒子的平均动能及太阳核心区的压强（请分别用eV和atm为单位）：(2)反应式(Il)中的x是什么粒子（α、β、γ、p和n之一）?请计算该粒子的动能和动量的大小，是否可以找到一个参照系，使得x粒子的动能为零？(3)给出反应式(I)中各反应产物的动能的范围：(4)反应式(IV)中的γ射线（光子）经过很多次的康普顿散射到达太阳表面的时候，其波长约为5.4xl0-7m．设入射光子的能量为E0，一次散射后光子的能量为E，光子的散射角为φ（出射光子动量相对于入射光子动量的夹角）．推导出由E和φ表示的E的表达式；假设从太阳中心到表面，光子经历了1026次康普顿散射，且每次散射的角度相同，求每一次的散射角φ．5