材料力学课件第七章弯曲应力.ppt

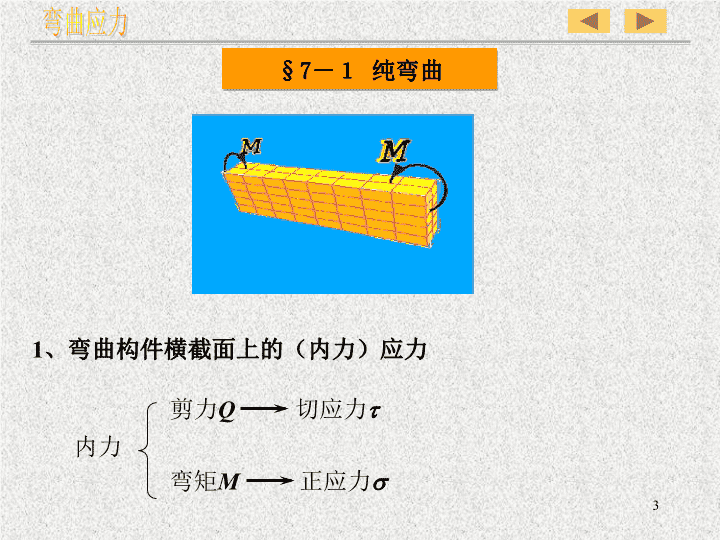
第七章弯曲应力材料力学1 §7–1纯弯曲§7–2纯弯曲时的正应力§7–3梁横截面上的切应力§7–4梁的正应力和切应力强度条件§7–5梁的合理截面第七章弯曲应力2 §7－１纯弯曲弯曲应力1、弯曲构件横截面上的（内力）应力内力剪力Q切应力t弯矩M正应力s3 平面弯曲时横截面s纯弯曲梁(横截面上只有M而无Q的情况)弯曲应力2、研究方法纵向对称面P1P2例如：平面弯曲时横截面t横力弯曲(横截面上既有Q又有M的情况)4 某段梁的内力只有弯矩没有剪力时，该段梁的变形称为纯弯曲。如AB段。弯曲应力PPaaABQMxx纯弯曲(PureBending):5 §7－2纯弯曲时的正应力1.纯弯曲实验①横向线(ab、cd）变形后仍为直线，但有转动；（一）梁的纯弯曲实验弯曲应力纵向对称面bdacabcdMM②纵向线变为曲线，且上缩下伸；③横向线与纵向线变形后仍正交。④横截面高度不变。6 纵向纤维间无挤压、只受轴向拉伸和压缩。平面假设：横截面变形后仍为平面，只是绕中性轴发生转动，距中性轴等高处，变形相等。2.推论弯曲应力3.两个概念中性层：梁内一层纤维既不伸长也不缩短，因而纤维不受拉应力和压应力，此层纤维称中性层。中性轴：中性层与横截面的交线。中性层纵向对称面中性轴（横截面上只有正应力）7 （二）几何方程：弯曲应力abcdABz)))OO1)横截面上任一点的纵向线应变与该点到中性层距离成正比（中性轴上应变为零，一侧拉应变，一侧压应变）A1B1O1Odqryy8 （三）物理关系：假设：纵向纤维互不挤压。于是，任意一点均处于单项应力状态。弯曲应力sxsx（四）静力学关系：①9 弯曲应力（∵y为对称轴，自动满足）……(3)EIz杆的抗弯刚度。②③中性层曲率：10 （五）最大正应力：弯曲应力……(5)DdDd=abhd11 例1受均布载荷作用的简支梁如图所示，试求：（1）1——1截面上1、2两点的正应力；（2）此截面上的最大正应力；（3）全梁的最大正应力；（4）已知E=200GPa，求1—1截面的曲率半径。弯曲应力Q=60kN/mAB1m2m11x+MM1Mmax12120180zy解：画M图求截面弯矩3012 弯曲应力Q=60kN/mAB1m2m11M1Mmax12120zy求应力18030x+M13 求曲率半径弯曲应力Q=60kN/mAB1m2m11M1Mmax1212018030x+M14 §7－3梁横截面上的切应力一、矩形截面梁横截面上的切应力1、两点假设：切应力与剪力平行；矩中性轴等距离处，切应力相等。2、研究方法：分离体平衡。在梁上取微段如图b；弯曲应力dxxQ(x)+dQ(x)M(x)yM(x)+dM(x)Q(x)dx图a图bzs1xys2t1tb图c在微段上取一块如图c，平衡15 弯曲应力dxxQ(x)+dQ(x)M(x)yM(x)+dM(x)Q(x)dx图a图b由切应力互等zs1xys2t1tb图c横力弯曲时,横截面上切应力的计算公式.16 弯曲应力zySz*为面积A*对横截面中性轴的静矩.式中:Q--所求切应力面上的剪力.IZ--整个截面对中性轴的惯性矩.Sz*--过所求应力点横线以外部分面积对中性轴的静矩.b--所求应力点处截面宽度.yA*yc*17 弯曲应力Qt方向：与横截面上剪力方向相同(不考虑正负号)；t大小：沿截面宽度均匀分布，沿高度h分布为抛物线。中性轴上有最大切应力.为平均切应力的1.5倍。二、其它截面梁横截面上的切应力1、研究方法与矩形截面同;切应力的计算公式亦为：其中Q为截面剪力；Sz为y点以下部分面积对中性轴之静矩；18 2、几种常见截面的最大弯曲切应力弯曲应力Iz为整个截面对z轴之惯性矩；b为y点处截面宽度。①工字钢截面：结论：翼缘部分tmax«腹板上的tmax，只计算腹板上的tmax。Af—腹板的面积。;»maxAQtf腹板最大弯曲切应力:d;»maxAQtf铅垂切应力主要腹板承受（95~97%），且tmax≈tmin故工字钢最大切应力19 ②圆截面：③薄壁圆环：④槽钢：弯曲应力exyzPQeQehHR20 §7-4梁的正应力和切应力强度条件1、危险面与危险点分析：一般截面，最大正应力发生在弯矩绝对值最大的截面的上下边缘上；最大切应力发生在剪力绝对值最大的截面的中性轴处。弯曲应力QtsssMt21 2、正应力和切应力强度条件：带翼缘的薄壁截面，最大正应力与最大切应力的情况与上述相同；还有一个可能危险的点，在Q和M均很大的截面的腹、翼相交处。（以后讲）弯曲应力3、强度条件应用：依此强度准则可进行三种强度计算：tsQtsM22 4、需要校核切应力的几种特殊情况：铆接或焊接的组合截面，其腹板的厚度与高度比小于型钢的相应比值时，要校核切应力。梁的跨度较短，M较小，而Q较大时，要校核切应力。各向异性材料（如木材）的抗剪能力较差，要校核切应力。、校核强度：Œ校核强度：设计截面尺寸：设计载荷：弯曲应力23 解：画内力图求危面内力例2矩形(bh=0.12m0.18m）截面木梁如图，[]=7MPa，[]=0.9MPa，试求最大正应力和最大切应力之比,并校核梁的强度。弯曲应力q=3.6kN/mABL=3mQ–+xx+qL2/8M24 求最大应力并校核强度应力之比弯曲应力q=3.6kN/mQ–+xx+qL2/8M25 y1y2GA1A2A3A4解：画弯矩图并求危面内力例3T字形截面的铸铁梁受力如图，铸铁的[L]=30MPa，[y]=60MPa，其截面形心位于G点，y1=52mm，y2=88mm，Iz=763cm4，试校核此梁的强度。并说明T字梁怎样放置更合理？4弯曲应力画危面应力分布图，找危险点P1=9kN1m1m1mP2=4kNABCDx-4kNm2.5kNmM26 校核强度T字头在上面合理。弯曲应力y1y2GA1A2y1y2GA3A4x-4kNm2.5kNmMA3A427 （一）矩形木梁的合理高宽比R北宋李诫于1100年著«营造法式»一书中指出:矩形木梁的合理高宽比(h/b=)1.5英(T.Young)于1807年著«自然哲学与机械技术讲义»一书中指出:矩形木梁的合理高宽比为弯曲应力bh§7-5梁的合理截面28 1、在面积相等的情况下，选择抗弯模量大的截面强度：正应力：切应力：(二)其它材料与其它截面形状梁的合理截面弯曲应力zDzaa29 弯曲应力zD0.8Da12a1z30 工字形截面与框形截面类似。弯曲应力0.8a2a21.6a22a2z31 对于铸铁类抗拉、压能力不同的材料，最好使用T字形类的截面，并使中性轴偏于抗变形能力弱的一方，即：若抗拉能力弱，而梁的危险截面处又上侧受拉，则令中性轴靠近上端。如下图：弯曲应力2、根据材料特性选择截面形状sGz32 弯曲应力（三）采用变截面梁，如下图：最好是等强度梁，即若为等强度矩形截面，则高为同时Px33 §5-5非对称截面梁的平面弯曲•开口薄壁截面的弯曲中心几何方程与物理方程不变。弯曲应力PxyzO34 依此确定正应力计算公式。切应力研究方法与公式形式不变。弯曲应力弯曲中心(剪力中心)：使杆不发生扭转的横向力作用点。（如前述坐标原点O）PxyzO35 槽钢：弯曲应力非对称截面梁发生平面弯曲的条件：外力必须作用在主惯性面内，中性轴为形心主轴，,若是横向力，还必须过弯曲中心。exyzPPsMQe36 弯曲中心的确定:(1)双对称轴截面，弯心与形心重合。(2)反对称截面，弯心与反对称中心重合。(3)若截面由两个狭长矩形组成，弯心与两矩形长中线交点重合。(4)求弯心的普遍方法：弯曲应力CCCQyeC37 ssss§5-6考虑材料塑性时的极限弯矩（一）物理关系为：全面屈服后,平面假设不再成立;仍做纵向纤维互不挤压假设。弯曲应力sessss理想弹塑性材料的s-e图ssss弹性极限分布图塑性极限分布图38 （二）静力学关系：（一）物理关系为：弯曲应力yzxssMjx横截面图正应力分布图39 弯曲应力yzxssMjx横截面图正应力分布图40 例4试求矩形截面梁的弹性极限弯矩Mmax与塑性极限弯矩Mjx之比。解：弯曲应力41 弯曲内力yzhb解：（1）横截面的切应力为：[例5]结构如图，试证明：（1）任意横截面上的切应力的合力等于该面的剪力；（2）任意横截面上的正应力的合力矩等于该面的弯矩；（3）过高度中点做纵截面，那么，此纵截面上的切应力的合力由哪个力来平衡？q42 弯曲内力(2)横截面上的合剪力为：(3)合力偶43 弯曲内力(4)中面上的切应力为：纵面上的合剪力与右侧面的正应力的合力平衡。(5)纵截面上的合剪力大小为：tmaxt¢44 本章结束45