静力学和材料力学课件第三章 力偶系(H).ppt

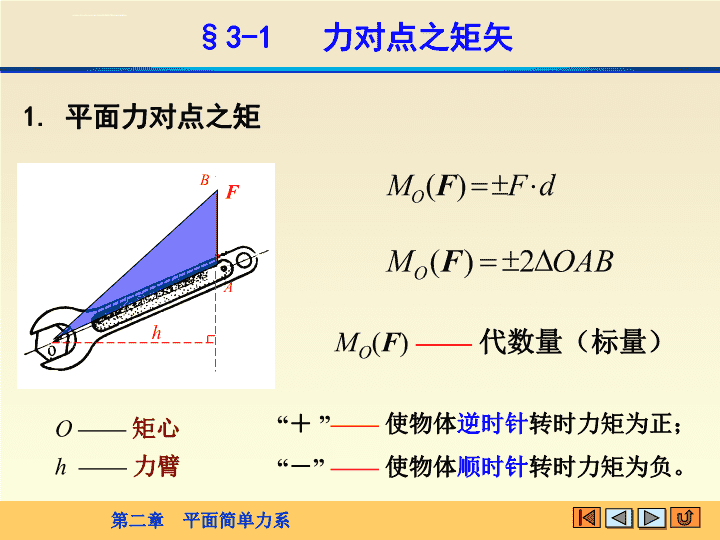
第3章力偶系※结论与讨论※力偶及其性质※力对轴之矩※力偶系的合成与平衡※力对点之矩矢 §3-1力对点之矩矢1.平面力对点之矩AFBhh——力臂O——矩心MO(F)——代数量（标量）“＋”——使物体逆时针转时力矩为正；“－”——使物体顺时针转时力矩为负。 2.合力之矩定理平面汇交力系合力对于平面内一点之矩等于所有各分力对于该点之矩的代数和。3.力矩与合力矩的解析表达式xAFFxFyOyxy FnOrFrF已知：Fn，，r求：力Fn块对轮心O的力矩。h解：（1）直接计算（2）利用合力之矩定理计算例题1 4.力对点的矩矢OA(x,y,z)BrFhyxzMO(F)空间的力对O点之矩取决于：（1）力矩的大小；（2）力矩的转向；（3）力矩作用面方位。★须用一矢量表征MO(F)=Fh=2△OAB OA(x,y,z)BrFhyxzMO(F)MO(F)定位矢量 BAFOxyzhFxybFz§3-2力对轴之矩Mz(F)★力对轴的矩等于力在垂直于该轴的平面上的投影对轴与平面交点的矩。Mz(F)=MO(Fxy)=±Fxyh=±2△OAb力对轴之矩用来表征——力对刚体绕某轴的转动效应。☆当力与轴在同一平面时，力对该轴的矩等于零。 yzOxFFxyA(x,y,z)FzFxFyFyFxBabxy力对轴之矩的解析表达式 3.力对点的矩与力对轴的矩的关系●力对点的矩矢在通过该点的某轴上的投影，等于力对该轴的矩。 Mz(F)(x,y,z)FxyMz(F)=MO(Fxy)=±2△Oab 求：MO(F)例题2已知：F、a、b、、解：(1)直接计算 (2)利用力矩关系 zFOabcAxy已知：F、a、b、c求：力F对OA轴之矩例题3MO(P)解：（1）计算MO(P)（2）利用力矩关系 §3-3力偶及其性质1.力偶与力偶矩力偶——两个大小相等、方向相反且不共线的平行力组成的力系。力偶臂——力偶的两力之间的垂直距离。力偶的作用面——力偶所在的平面。 （1）力偶不能合成为一个力，也不能用一个力来平衡。力和力偶是静力学的两个基本要素。（2）力偶矩是度量力偶对刚体的转动效果；它有两个要素：力偶矩的大小和力偶矩的转向。ABOdx 2.平面力偶的等效定理F0F0ABDCdFF1F2★在同平面内的两个力偶，如果力偶矩相等，则两力偶彼此等效。推论1：力偶对刚体的作用与力偶在其作用面内的位置无关。推论2：只要保持力偶矩的大小和力偶的转向不变，可以同时改变力偶中力的大小和力偶臂的长短，而不改变力偶对刚体的作用。MMM §3-4空间力偶(1)力偶矩的大小；(2)力偶的转向；(3)力偶作用面的方位。M自由矢量空间力偶的定义:空间力偶的等效条件两个力偶的力偶矩矢相等，则它们是等效的。AFBM M=M1+M2+…+Mn=∑Mi空间力偶系的合成与平衡合力偶矩矢： 平衡条件平衡方程平面力偶系的平衡方程 MaaABCa求：A、C处约束反力。已知：a,M解：（1）取AB为研究对象（2）取BC为研究对象BCABMFBFCFA例题4 M1M2CABDM2CDM1ABFBFAFCFD解:(1)取AB为研究对象(2)取CD为研究对象求：平衡时M1、M2之间的关系。已知：AB=CD=a,∠BCD=30°解得解得因为FB=FC例题5 DBCMDEEDCBAMaaaa求：A、B、C、D、E处的约束反力。解:(1)取整体为研究对象FAFB(2)取BCD为研究对象FBFEFD(3)取DE为研究对象确定D处约束反力的方向例题6 DBCMDEFBFEFD(3)取DE为研究对象CAEFC(4)取ACE为研究对象FA ADCB问刚体在四个力的作用下是否平衡，若改变F1和F1′的方向，则结果又如何。思考题1 Ro当M=PR时，系统处于平衡，因此力偶也可以与一个力平衡，这种说法对吗。思考题2 ABC图示系统平衡否，若平衡，A、B处约束反力的方向应如何确定。思考题3 1.力矩的计算（1）力对点的矩OA(x,y,z)BrFhyxzMO(F)MO(F)=Fh=2△OAB结论与讨论 OABabFFxyhz●力对轴的矩等于力在垂直于该轴的平面上的投影对轴与平面交点的矩。Mz(F)=Mo(Fxy)=±Fxyh=±2△oab（2）力对轴的矩yzOxFFxyA(x,y,z)FzFxFyFyFxBabxy （3）力对点的矩与力对轴的矩的关系●力对点的矩矢在通过该点的某轴上的投影，等于力对该轴的矩。2.合力矩定理●力系的合力对任一点（或任一轴）之矩等于力系中各力对同一点（或同一轴）之矩的矢量和（代数和）。 3.空间力偶及其等效条件(1)力偶矩的大小；(2)力偶的转向；(3)力偶作用面的方位。M自由矢量空间力偶的定义:空间力偶的等效条件:两个力偶的力偶矩矢相等，则它们是等效的。AFBM 4.空间力偶的合成与平衡M=M1+M2+…+Mn=∑Mi合力偶矩矢： 平衡条件平衡方程平面力偶系的平衡方程 谢谢使用