材料力学课件4.（剪力弯矩图，微分关系）.pdf

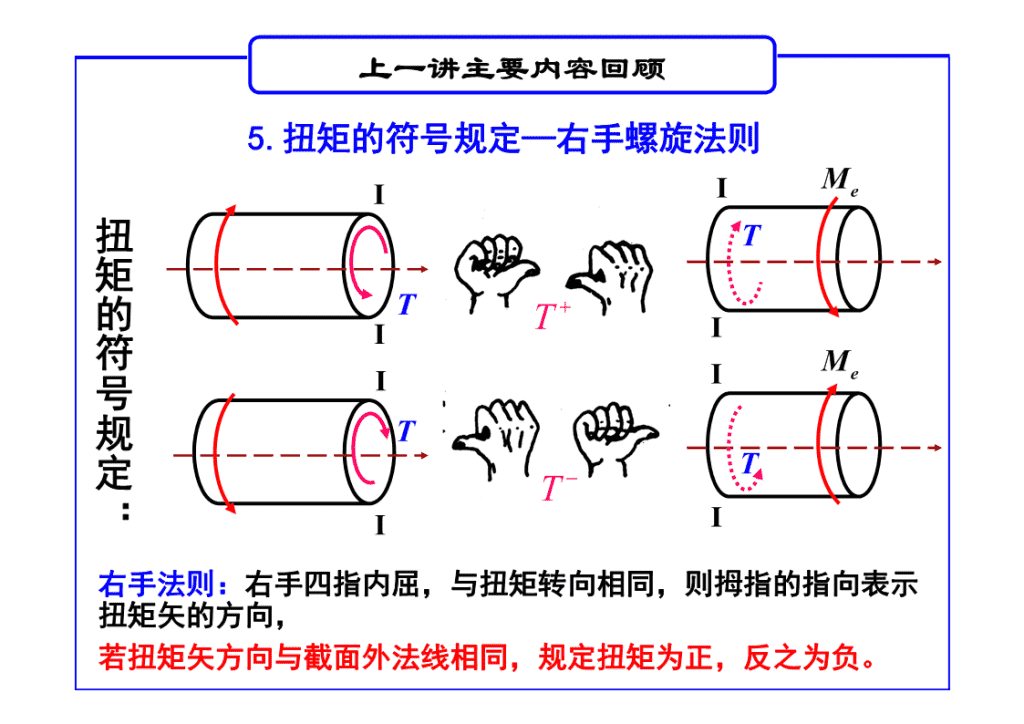
哈尔滨工业大学本科生课第2章内力及内力图§2.6内力图——剪力图与弯矩图§2.7弯矩、剪力和分布荷载之间的关系§2.8利用弯矩、剪力和载荷的关系作剪力图和弯矩图 上一讲主要内容回顾5.扭矩的符号规定—右手螺旋法则M扭矩的符号规定：IIeTTTIIMIIeTTTII右手法则：右手四指内屈，与扭矩转向相同，则拇指的指向表示扭矩矢的方向，若扭矩矢方向与截面外法线相同，规定扭矩为正，反之为负。 上一讲主要内容回顾1.平面弯曲受力特点：垂直于轴线的所有外力（载荷和支座反力）作用在纵向对称面内。变形特点：轴线由直线变成了在纵向对称面内的平面曲线。 上一讲主要内容回顾工程中，常见的三种静定梁的计算简图：简支梁一端是固定铰支约束另一端可动铰支约束悬臂梁一端为固定端另一端自由外伸梁绞支座支撑梁的一端或两端伸于支座之外 上一讲主要内容回顾FMs剪力和弯矩的正负号规则：左上右下为正FsFsFsFs上压下拉为正向下凸出为正MMMM 哈尔滨工业大学本科生课§2.6内力图——剪力图和弯矩图 §2.6内力图——剪力和弯矩图1.剪力方程和弯矩方程横截面的位置用梁的轴线坐标x表示各横截面上的剪力和弯矩就可以表示成x的函数FF=()x剪力方程ssMM=()x弯矩方程FFFsMFx()=-FsxlMx()=-Fx §2.6内力图——剪力和弯矩图2.剪力图和弯矩图以横坐标x表示梁的截面位置，纵坐标表示剪力和弯矩的数值剪力图--正的剪力画在x轴上方，负的剪力图画在下方土木工程:负弯矩画在x轴上方弯矩图（两种做法）机械工程:正弯矩画在x轴上方FFFsMF(x)FsxlM(x)Fx §2.6内力图——剪力和弯矩图FFFsMF(x)FsxFlM(x)Fxs剪力图弯矩图Flxx00FM2.剪力图和弯矩图以横坐标x表示梁的截面位置，纵坐标表示剪力和弯矩的数值剪力图--正的剪力画在x轴上方，负的剪力图画在下方土木工程:负弯矩画在x轴上方弯矩图（两种做法）机械工程:正弯矩画在x轴上方 §2.6内力图——剪力和弯矩图例1q解：利用对称性,支反力ABR=R=ql/2ABlqRRBAMqlRF2AsxFsqll/2剪力方程Fql/2qx2sql12弯矩方程Mxqx22M2ql8 §2.6内力图——剪力和弯矩图例2Fl/323l/解:1)求约束反力,并验算ABC21R=FR=FABRRB33A2)分段列剪力与弯矩方程FslAM0xAC段：2l3F(x)F(0x)RsAx332lM(x)Fx(0x)33MBC段：xFRB1lsF(x)F(xl)slx33lxlFlM(x)(lx)(xl)333 §2.6内力图——剪力和弯矩图例2Fl/323l/解:1)求支座反力,并验算ABC21RFFRABRRB33A3）作剪力图与弯矩图2)分段列剪力与弯矩方程2F3AC段：2lF(x)F(0x)s33Fs1F2l3M(x)Fx(0x)33BC段：1lF(x)F(xl)s33M2FlFlM(x)(lx)(xl)933 §2.6内力图——剪力和弯矩图例2Fl/323l/ABCRRBA3）作剪力图与弯矩图在集中力作用处，2F剪力图发生突变，其突变3量就等于集中力的数值；Fs1F弯矩连续，但弯矩图在此3出现转折（斜率不同的点）M2Fl9 §2.6内力图——剪力和弯矩图例3mC解：1)求支座反力ABabmmlRRABllRRB2)分段列内力方程AAC段()0xaFsAM0xammF(x)M(x)xsRllAxBCB段()axlMxFRBmsFx()sllxmmaxlMxlxz()=mxll §2.6内力图——剪力和弯矩图例3mC解：1)求支座反力ABabmmlRRABllRRB2)分段列内力方程AAC段()0xa3）作剪力图与弯矩图mmmF(x)M(x)xsllFamlsCB段()axllmFx()sMlbmmmlMxlxz()=mxll §2.6内力图——剪力和弯矩图例3mCABabl在集中力偶作用处，RRBA剪力连续，3）作剪力图与弯矩图弯矩发生突变，其突m变量就等于集中力偶Famls矩的值。lMbml §2.6内力图——剪力和弯矩图控制截面——外力规律发生变化的截面1.集中力、集中力偶作用点；2.分布载荷的起点和终点处的横截面。MqF0EADBCFBy1m1m2m1m1mFAy 哈尔滨工业大学本科生课§2.7弯矩、剪力与载荷集度之间的微分关系 §2.7弯矩、剪力与载荷集度之间的微分关系设梁上作用有任意载荷分布载荷集度为q()xq()xq()x方向规定:向上为正M()xMx()dMx()q()xFs(x)Fs(x)dFs(x)xdxdx §2.7弯矩、剪力与载荷集度之间的微分关系Fy0Fs(x)q(x)dxFs(x)dFs(x)dFx()sq()xqx()dxM()xMx()dMx()剪力函数的一阶导数x等于分布载荷集度F(x)F(x)dF(x)syss §2.7弯矩、剪力与载荷集度之间的微分关系Mc012M()()xFxxqxdd=()xMxMx()d()s212q()x忽略高阶小量qxdx()2M()xMx()dMx()dMx()F()xsdxxc弯矩函数的一阶导数等于剪力函数F()xF()d()xFxsyss §2.7弯矩、剪力与载荷集度之间的微分关系微分关系几何意义d()Fx剪力图上某点处切线的斜率等sqx()于梁上该点处的分布载荷集度qdxd()MxFx()弯矩图上某点处切线的斜率等sdx于梁上该点处截面上的剪力Fs2d()Mxqx()弯矩图的凹向取决于分布载荷2dx集度q的正负 §2.7弯矩、剪力与载荷集度之间的微分关系分布载荷、剪力图和弯矩图之间的规律1.梁段上无分布载荷：剪力图切线斜率为零dFx()s(1)qx()0dxFs为常数，剪力图为平直线dMx()弯矩为一次函数(2)F()x常数sdx弯矩图直线0弯矩图为平直线Fs()x0弯矩为增函数下斜直线0弯矩为减函数，上斜直线 §2.7弯矩、剪力与载荷集度之间的微分关系分布载荷、剪力图和弯矩图之间的规律1.梁段上无分布载荷：若梁段没有分布载荷，只有集中力和集中力偶剪力图和弯矩图不可能出现曲线图形其中剪力必为常数，弯矩可能是常数或一次函数 §2.7弯矩、剪力与载荷集度之间的微分关系分布载荷、剪力图和弯矩图之间的规律2.梁段上的分布载荷为不等于零的常数dFx()剪力为一次函数s(1)qx()常数0dx剪力图为斜直线0剪力为增函数，上斜直线qx()0剪力为减函数，下斜直线 §2.7弯矩、剪力与载荷集度之间的微分关系分布载荷、剪力图和弯矩图之间的规律2.梁段上的分布载荷为不等于零的常数dMx()(1)F()x一次函数sdxM()x为二次函数，弯矩图为二次曲线M()x应有极小值0弯矩图为上凸曲线qx()M()x应有极大值0弯矩图为下凸曲线 §2.7弯矩、剪力与载荷集度之间的微分关系分布载荷、剪力图和弯矩图之间的规律2.梁段上的分布载荷为不等于零的常数M()x极值的位置在Fx()0的截面sM()x应有极小值0弯矩图为上凸曲线qx()M()x应有极大值0弯矩图为下凸曲线 §2.7弯矩、剪力与载荷集度之间的微分关系q例1ABlRRBAql2Fsqll/22M2ql8 §2.7弯矩、剪力与载荷集度之间的微分关系例2例3mFl/323l/CABABCabRRBAl2F3RRBAmFs1FamlFs3lMMbm2Fll9 哈尔滨工业大学本科生课§2.8利用M、F与q的微分关系作s剪力图和弯矩图 §2.8利用微分关系作剪力、弯矩图作图要点：(1)计算支反力，并在梁上标出其实际方向(2)利用微分关系，确定剪力和弯矩图的形状(3)考虑集中力、集中力偶的位置，剪力和弯矩的突变自左向右剪力突变方向与集中力方向相同顺时针转向的弯矩使弯矩图向下突变(4)计算控制截面上的剪力和弯矩值(5)验算，剪力图和弯矩图自左端到右端应封闭 §2.8利用微分关系作剪力、弯矩图例1q作图要点：(1)计算支反力，标出其实际方向ABl(2)利用微分关系，确定形状RRBAR=R=ql/2(3)考虑集中力、集中力偶的突变ABql2自左向右剪力突变方向与集中力方向相同Fsqll/2顺时针转向的弯矩使弯矩图向下2突变(4)计算控制截面值M2ql(5)验算，自左端到右端应封闭8 §2.8利用微分关系作剪力、弯矩图作图要点：例2Fl/323l/(1)计算支反力，标出其实际方向ABC(2)利用微分关系，确定形状2RRFA=RBA3(3)考虑集中力、集中力偶的突变2FFR=3B3自左向右剪力突变方向与集中力方向相同Fs顺时针转向的弯矩使弯矩图向下F突变3(4)计算控制截面值M2(5)验算，自左端到右端应封闭Fl9 §2.8利用微分关系作剪力、弯矩图作图要点：例3mC(1)计算支反力，标出其实际方向ABab(2)利用微分关系，确定形状l(3)考虑集中力、集中力偶的突变Rml/Rml/AB自左向右剪力突变方向与集中力方向相同mFamls顺时针转向的弯矩使弯矩图向下突变l(4)计算控制截面值Mbm(5)验算，自左端到右端应封闭l §2.8利用微分关系作剪力、弯矩图利用剪力、弯矩与分布荷载间的积分关系定值dFxsdMxqxFsxdxdxdF(x)q(x)dxdM(x)F(x)dxssxxxx2222dF(x)q(x)dxdM(x)F(x)dxxxsxxs1111x2x2FFq(x)dxMMF(x)dxs2s121xsx11任意两截面的剪力差==两截面间任意两截面的弯矩差==两截分布载荷图所包围的面积面间剪力图所包围的面积 §2.8利用微分关系作剪力、弯矩图例1qx2FFq(x)dxs2s1ABx1lRRB任意两截面的剪力差==两截AR=R=ql/2AB面间分布载荷图所包围的面积ql2Fx2sqlMMF(x)dxl/221xs21任意两截面的弯矩差==两截M2面间剪力图所包围的面积ql8 §2.8利用微分关系作剪力、弯矩图例2例3mFl/323l/CABABCabRRBAl2F3RRBAmFsFFamls3lMMbm2Fll9 §2.8利用微分关系作剪力、弯矩图q例1AClBl/2qlR5qlRBRAqlB882④Fs③①ql②2ql8①8②M §2.8利用微分关系作剪力、弯矩图例2q3qlACBRl/2l/2Aql83qlRB88F②s①④ql③8M①③29ql2②ql16128 哈尔滨工业大学本科生课作业教材44页：2.10（b)、(d)、(f)、(g)