材料力学课件ppt-6弯曲变形

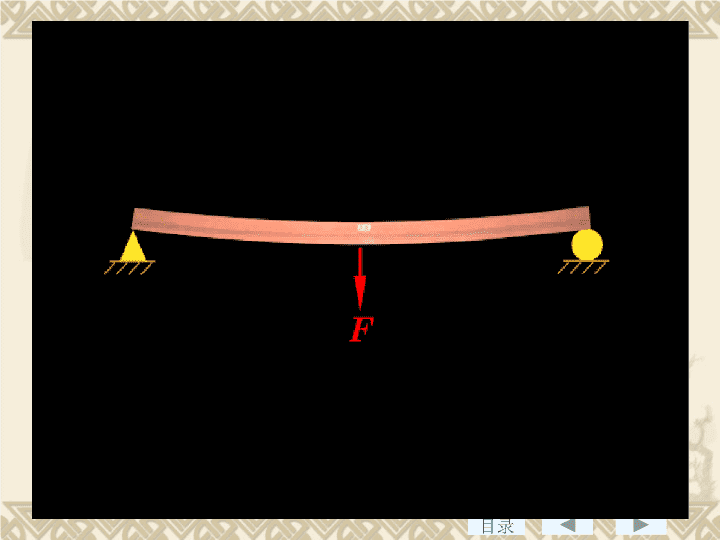
第六章弯曲变形§6-1工程中的弯曲变形问题§6-2挠曲线的微分方程§6-3用积分法求弯曲变形§6-4用叠加法求弯曲变形§6-5简单超静定梁§6-6提高梁刚度的措施目录目录 目录§6-1工程中的弯曲变形问题 目录 目录 目录 目录 §6-2挠曲线的微分方程一.基本概念1、挠曲线方程：由于小变形，截面形心在x方向的位移忽略不计4、挠度转角关系为：挠曲线挠度转角2、挠度ω：截面形心在y方向的位移ω向上为正3、转角θ：截面绕中性轴转过的角度。逆时针为正6-2目录 二、挠曲线的近似微分方程力学公式数学公式以上两式消去，得：目录 小挠度情形下：弯曲变形/挠曲线的近似微分方程目录 yy符号规定：MM因此（挠曲线的近似微分方程）弯曲变形/挠曲线的近似微分方程目录 由挠曲线的近似微分方程积分一次：（转角方程）积分二次：（挠度方程）式中C、D为积分常数，由梁的约束条件决定。§6-3用积分法求弯曲变形目录 悬臂梁：xyAB梁的边界条件简支梁：xyABL目录 PABC梁的连续条件：ABlaCM目录 例如：写出下图的边界条件、连续性条件：ALFCabBEAhDALFCabkBxy 讨论：挠曲线分段处（1）凡弯矩方程分段处，应作为分段点；（2）凡截面有变化处，或材料有变化处，应作为分段点；（3）中间铰视为两个梁段间的联系，此种联系体现为两部分之间的相互作用力，故应作为分段点；ABlaCM目录 ABlaCM（4）凡分段点处应列出连续条件，根据梁的变形的连续性，对同一截面只可能有唯一确定的挠度和转角；在中间铰两侧虽然转角不同，但挠度却是唯一的。目录 AqBL例6-1悬臂梁受力如图所示。求和。xyx取参考坐标系Axy。解：1、列出梁的弯矩方程2、积分一次：积分二次：（1）（2）目录 3、确定常数C、D.由边界条件：代入（1）得：代入（2）得：代入（1）（2）得：目录 代入得：将（与C比较知：）（与D比较知：）常数C表示起始截面的转角×刚度(EI)因此常数D表示起始截面的挠度×刚度(EI)目录 例6-2一简支梁受力如图所示。试求和。ALFCabyx解：1、求支座反力x2、分段列出梁的弯矩方程BC段xAC段B目录 BC段AC段3、确定常数由边界条件：（1）（2）由光滑连续条件：（3）（4）可解得：目录 则简支梁的转角方程和挠度方程为BC段AC段4、求转角代入得：代入得：目录 5、求。求得的位置值x。则由解得：目录 代入得：若则：在简支梁情况下，不管F作用在何处（支承除外），可用中间挠度代替，其误差不大，不超过3%。目录 一、叠加法前提小变形力与位移之间的线性关系挠度、转角与载荷（如P、q、M）均为一次线性关系轴向位移忽略不计。§6-4用叠加法求弯曲变形目录 叠加原理：在小变形和线弹性范围内，由几个载荷共同作用下梁的任一截面的挠度和转角，应等于每个载荷单独作用下同一截面产生的挠度和转角的代数和。例6-4已知：q、l、EI，求：yC,B第一类叠加法应用于多个载荷作用的情形目录 www目录 www弯曲变形/用叠加法求梁的变形目录 目录 例6-5怎样用叠加法确定C和yC?w目录 wwww目录 ww目录 w目录 第二类叠加法逐段分析法将梁的挠曲线分成几段，首先分别计算各段梁的变形在需求位移处引起的位移（挠度和转角），然后计算其总和（代数和或矢量和），即得需求的位移。在分析各段梁的变形在需求位移处引起的位移时，除所研究的梁段发生变形外，其余各段梁均视为刚体。ABalFC例6-6：怎样用叠加法确定yC?目录 ABalFC例6-6：FABalCFaFaBC+1）考虑AB段(BC段看作刚体)F作用在支座上，不产生变形。Fa使AB梁产生向上凸的变形。查表得：则怎样用叠加法确定wC?目录 2）考虑BC段(AB段看作刚体)AFaBC所以ABalCFa目录 刚度条件：[y]——许用挠度，[]——许用转角工程中，[y]常用梁的计算跨度l的若干分之一表示，例如：对于桥式起重机梁：对于一般用途的轴：在安装齿轮或滑动轴承处，许用转角为：目录 静不定梁—未知力的数目多于能列出的独立平衡方程的数目，仅利用平衡方程不能解出全部未知力，则称为超静定问题（或静不定问题）。静不定次数=未知力的数目-独立平衡方程数BqL4个约束反力，3个平衡方程，静不定次数=1§6-5简单超静定梁目录 用力法求解静不定问题的步骤：1、确定静不定次数。2、选择基本静定梁。静定梁(基本静定基)—将静不定梁的多余约束解除，得到相应的静定系统，该系统仅用静力平衡方程就可解出所有反力以及内力。多余约束—杆系在维持平衡的必要约束外所存在的多余约束或多余杆件。多余约束的数目=超静定次数BqL多余约束的数目=1目录 静定梁(基本静定基)选取(2)解除A端阻止转动的支座反力矩作为多余约束,即选择两端简支的梁作为基本静定梁。BqLA(1)解除B支座的约束,以代替，即选择A端固定B端自由的悬臂梁作为基本静定梁。BqLA目录 (2)基本静定基要便于计算，即要有利于建立变形协调条件。一般来说，求解变形时，悬臂梁最为简单，其次是简支梁，最后为外伸梁。基本静定基选取可遵循的原则：(1)基本静定基必须能维持静力平衡，且为几何不变系统；目录 ABqLBqLABqLA3、列出变形协调条件。比较原静不定梁和静定基在解除约束处的变形，根据基本静定梁的一切情况要与原超静定梁完全相同的要求，得到变形协调条件。目录 本例：(1)4、用积分法或叠加法求变形，并求出多余未知力。仅有q作用，B点挠度为：仅有作用，B点挠度为：因此解得:BqlA目录 5、根据静力平衡条件在基本静定梁上求出其余的约束反力。本例：(1)BqLA（）目录 BqLA(+)(-)BqL因此6、在基本静定梁上按照静定梁的方法求解内力、应力和变形。目录 解例6求梁的支反力，梁的抗弯刚度为EI。1）判定超静定次数2）解除多余约束，建立相当系统目录3）进行变形比较，列出变形协调条件 4）由物理关系，列出补充方程所以4）由整体平衡条件求其他约束反力目录 例7梁AB和BC在B处铰接，A、C两端固定，梁的抗弯刚度均为EI，F=40kN，q=20kN/m。画梁的剪力图和弯矩图。从B处拆开，使超静定结构变成两个悬臂梁。变形协调方程为：FBMAFAyB1FBMCFCyB2物理关系解目录 FBFBMAFAMCFCyB1yB2代入得补充方程：确定A端约束力目录 FBF´BMAFAMCFCyB1yB2确定C端约束力目录 MAFAMCFCA、B端约束力已求出最后作梁的剪力图和弯矩图目录 梁的变形除了与载荷与梁的约束有关外，还取决于以下因素：材料——梁的变形与弹性模量E成反比；截面——梁的变形与截面的惯性矩成反比；跨长——梁的变形与跨长l的n次幂成正比§6-6提高梁刚度的措施目录 1）选择合理的截面形状目录 2）改善结构形式，减少弯矩数值改变支座形式目录 2）改善结构形式，减少弯矩数值改变载荷类型目录 3）采用超静定结构目录 3）采用超静定结构目录