材料力学课件8

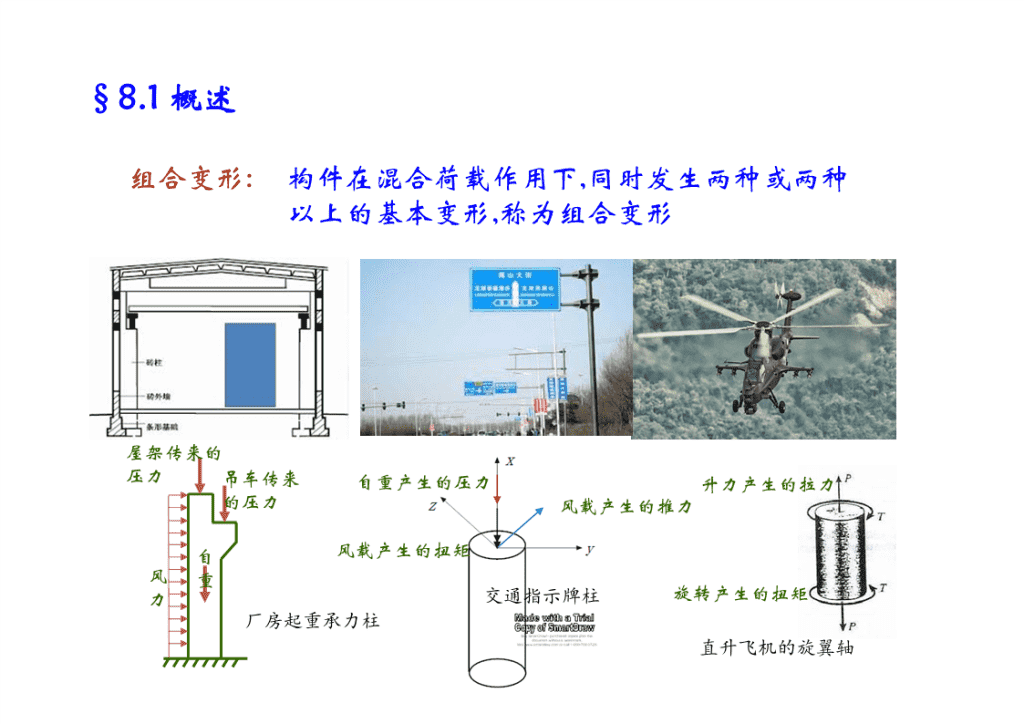
第八章组合变形及连接部分的计算Chapter8CombinedDeformationsandApproximatedAnalysisforConnectingParts §8-1概述§8-2两相互垂直平面内的弯曲§8-3拉伸（压缩）与弯曲§8-4扭转与弯曲§8-5连接件的实用计算法 §8.1概述组合变形:构件在混合荷载作用下,同时发生两种或两种以上的基本变形,称为组合变形屋架传来的压力吊车传来自重产生的压力升力产生的拉力的压力风载产生的推力自风载产生的扭矩风重力交通指示牌柱旋转产生的扭矩厂房起重承力柱直升飞机的旋翼轴 组合变形强度计算的步骤:1.外力分析将荷载简化为符合基本变形外力作用条件的静力等效力系2.内力分析分别做出各基本变形的内力图,确定构件危险截面位置及其相应内力分量,按叠加原理画出危险点的应力状态图.3.应力分析按危险截面上的内力值，分析危险截面上的应力分布，确定危险点所在位置。4.强度分析根据危险点的应力状态和杆件的材料按强度理论进行强度计算。 §8.2两相互垂直平面内的弯曲回顾：单平面弯曲纵向对qM称面Fez中性轴BAxy纵向对称轴yMyMzz[]maxxIWzz F2两相互垂直平面z内的弯曲xF1yMzMyyzx1x1x2IIMyzzmaxMFxz21MzMyyzxxx12IIyzMFxMy11ymaxx1x2xMMyz 中性轴位置：0x令y，z代表中性轴上任一点的坐标00Myz0Mzy0z0MzIyIy0tgtg合弯矩线IyIzy0MyIzIzMyIItgtgyzM斜弯曲时，横截面的中性轴是一条通过截面zz形心的斜直线。一般情况下，中性轴不与外(,)yz00力垂直合力线y中性轴（注：合外力线垂直于合弯矩线） 强度校核：(1)选择危险截面:MymaxMzmax(2)根据应力分布选择危险点MyMyMzzzMzzyyyMymaxMzmaxMymaxMzmaxx1x2maxWminWWyzWyz 例题一般生产车间所用的吊车大梁,两端由钢轨支撑,可以简化为简支8.1梁,如图示.图中L＝4m。大梁由32a热轧普通工字钢制成，许用应力［σ］＝160MPa。起吊的重物重量F＝80kN，且作用在梁的中点，作用线与y轴之间的夹角α＝5°，试校核吊车大梁的强度是否安全。F解：（1）首先将斜弯曲分解为两个平面弯曲的叠加FFyFcosMMyzWWzyzFFsinzL2L2危险点zMzy（2）确定危险截面:两个平面弯曲的最大弯矩及作用位置FyLFzLMyMzMyy44(注：弯矩图可以不考虑正负，但是要知道拉压侧的位置)（3）计算最大正应力并校核强度查表：33W692.2cmW70.758cmyzMyMz217.8MPamaxWWyz(217.8-115.6)/115.6*100%=88.41％（4）讨论0115.6MPamax吊车起吊重物只能在吊车大梁垂直方向起吊，不允许在大梁的侧面斜方向起吊。 §8.3拉伸（压缩）与弯曲横向力与轴向力共同作用qzMzFFFNABlMz+=FNFNMymaxNMAIZFMyNzmaxAIminZ 例题设图示简易吊车在当小车运行到距离梁端D还有0.4m8.2处时，吊车横梁处于最不利位置。已知小车和重物的总重量F＝20kN，钢材的许用应力［σ］＝160MPa，暂不考虑梁的自重。按强度条件选择横梁工字钢的型号。FFByBFAxFBxFAyF49.7kNB左截面压应力最大30kNmFMNzmaxAWzM3试算：不考虑轴力的影响：z187.5WcmzW查表并考虑轴力的影响：z3649.710301032[]20aWz237cmA35.5cmmax35.5102237103140.6MPa 例题一桥墩如图示。承受的荷载为：上部结构传递8.3给桥墩的压力F＝1920kN，桥墩墩帽及墩身的自0重F＝330kN，基础自重F＝1450kN，车辆经梁12部传下的水平制动力F＝300kN。试绘出基础底T部AB面上的正应力分布图。已知基础底面积为b×h＝8m×3.6m的矩形。FFFF3700kN3700kNN0121740kNmMF5.81740kNmmaxTFNMzy0.027MPamax0.229minAIZ0.229MPa0.027 例题一受拉弯组合变形的圆截面钢轴，若用第三强度理论8.4设计的直径为d，用第四强度理论设计的直径为d，则34d3_____＝d4。（填“＞”、“＜”或“＝”）因受拉弯组合变形的杆件，危险点上只有正应力，而无切应力，224r3131222223r41223312r3r4 例题8.5如图示一矩形截面折杆，已知F＝50kN，尺寸如图所示，α＝30°。（1）求B点横截面上的应力（2）求B点α＝30°截面上的正应力；（3）求B点的主应力σ、σ、σ、。123600mm（1）M400Fcos200FsinB200Fsin71.2310Nmm400mm3FsinFFNsin2510BN200mmBMFBBN100mmWAFsin18.451.25MPaMPa200mm17.2(压应力)FMPaFcos（2）（3）0017.3201cos6012.9MPa1302B0217.23MPa3 偏心拉伸（压缩）单向偏心拉伸（压缩）FeFFMFeMFeFFeyNAIZFNMFezAByFABeFMFe单向偏心压缩时,距偏心力较近的一侧边缘总是产生压应力,而最大正应力总是发生在距偏心力较远的另一侧,其值可能是拉应力,也可能是压应力. 双向偏心拉伸（压缩）1.外力分析zzeyFFMFe2.内力分析zyezFFyyNMyFezEy,zDCMFeyzABMFezyFNMyMzAAWWyz3.应力计算FNMyMzFNMyzMzyBAWyWzAIIyzFNMyMzCAWWyzFNMyMzDAWWyz 例题图示矩形截面钢杆，用应变片测得杆件上、下8.6表面的轴向正应变分别为ε＝1×10－3、ε＝ab0.4×10－3，材料的弹性模量E＝210GPa。(1).试绘出横截面上的正应力分布图；(2).求拉力F及偏心距δ的距离。210MPaa5FF25b84MPaE210MPaaabhF18.38kNbEb84MPaab2FNMF6FaAWbhbh22bhabFMF6F1.786mmN12Fb2AWbhbh §8.4扭转与弯曲F（1）利用内力图确定危险截面TMmaxmaxzmaxAmaxWWPazL（2）危险截面上危险点处的应力状态FAFaAσστBFLBτFa （3）强度理论校核A点：22xx1，322x第三强度理论22413222222MTMTMTzzmaxmaxmaxmaxzmaxmax4[]WWWWWzpzzz第四强度理论12222212233132222222MTMT3MT0.75zzmaxmaxmaxmaxzmaxmax3[]WWWW4Wzpzzz 例题8.7图示圆轴.已知,F=8kN,M=3kNm,［σ］=100MPa,试用第三强度理论求轴的最小直径.解：（1）利用内力图确定危险截面危险截面FMFL4kNmTk3Nm危险点（2）危险截面上危险点处的应力状态MmaxT0.5mMmaxWzWpT图（3）强度理论校核224M图22MTzWz22MzT5332WzWz510md379.8mm 拉伸（压缩）＋弯曲斜弯曲弯曲＋扭转拉伸（压缩）弯曲扭转FNMMyMzMT单向应力状态复杂应力状态强度理论强度条件maxr §8.5连接件的实用计算FmmFF螺栓连接m-mFF冲孔销轴连接 I.剪切FFsFsF剪切：位于两力间的截面发生相对错动受力特点：作用在构件两侧面上的外力的合力大小相等、方向相反、作用线相距很近。 sss在计算中，要正确确定有几个剪切面，以及每个剪切面上的剪切力。 假设切应力在剪切面上是均匀分布的,得实用切应力计算公式：FF--剪切面上的剪切力ssAsA--剪切面的面积sF切应力强度条件：sAs许用切应力，常由实验方法确定塑性材料：0.50.7脆性材料：0.81.0 II.挤压挤压面FFFbsFbsd挤压力最大挤压应力挤压：挤压是构件相互压紧的现象受力特点：接触面存在作用和反作用力在圆弧挤压面上挤压应力非均匀分布 实际FbsmaxbsAδbsFdAbs[]bs切应力强度条件：bsbsAbs许用挤压应力，常由实验方法确定bs塑性材料：1.52.5bs脆性材料：0.91.5bs*注意挤压面面积的计算（1）接触面为平面（2）接触面为圆柱面A—实际接触面面积A—挤压面在垂直于挤bsbs压方向上的投影面积 例题图示钢板铆接件，已知钢板拉伸许用应力［σ］＝98MPa，8.8挤压许用应力［σ］＝196MPa，钢板厚度δ＝10mm，bs宽度b＝100mm，铆钉直径d＝17mm，铆钉许用切应力［τ］＝137MPa，挤压许用应力［σ］＝314MPa。若bs铆接件承受的载荷F＝23.5kN。试校核钢板与铆钉的强度。P 拉伸强度FF23.5103NP28.3MPaA(bd)(10017)10 挤压强度F3P23.510bs138MPabsd1710 剪切强度（对于铆钉）FPF3s22FP223.510251.8MPaAd22d3.14174 例题8.9图示拉杆头和拉杆的横截面均为圆形，拉杆头的剪切面积A＝（B）。222A.DhB.dhC.d4D.Dd4 例题图示木杆接头，已知轴向力F＝50kN，截面8.10宽度b＝250mm，木材的顺纹挤压容许应力[σ]＝10MPa，须纹许用切应力[τ]＝1MPa。bs试根据剪切和挤压强度确定接头的尺寸L和a。FFSbAlbFFa3F5010L200mmb2501LL挤压面FFbsbsbsAbaFFbsF50103剪切面a20mmbbs25010