北大材料力学课件ch3扭转

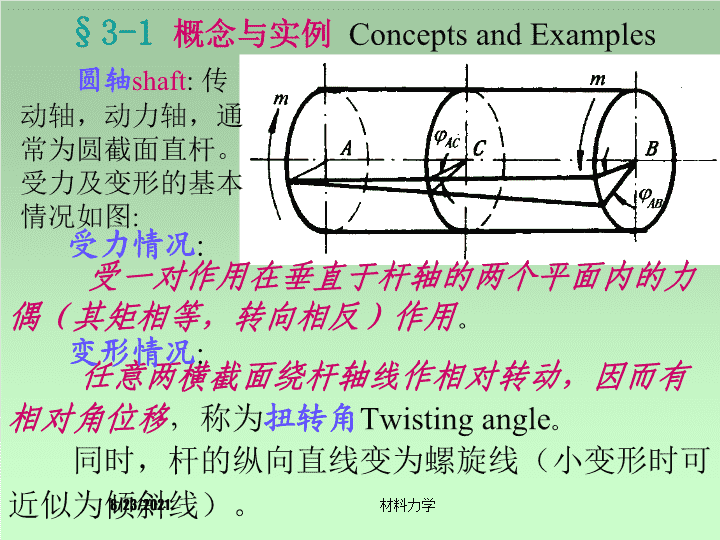
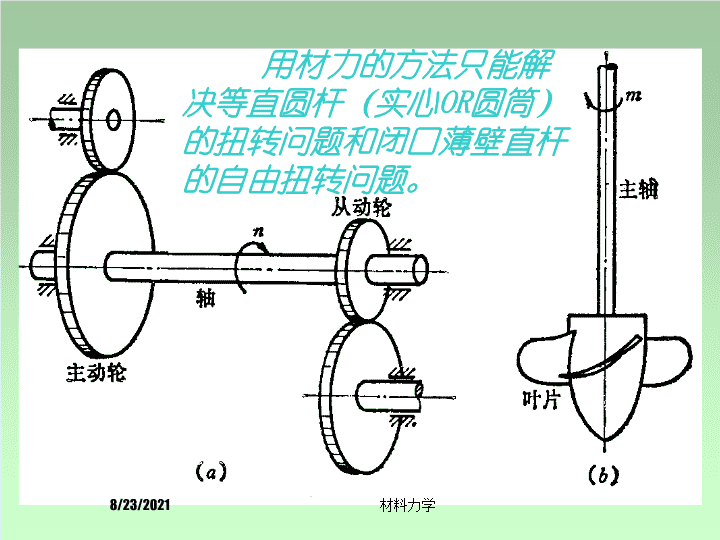
材料力学第三章扭转Torsion8/23/2021材料力学 §3-1概念与实例ConceptsandExamples圆轴shaft:传动轴，动力轴，通常为圆截面直杆。受力及变形的基本情况如图:受一对作用在垂直于杆轴的两个平面内的力偶（其矩相等，转向相反）作用。受力情况:任意两横截面绕杆轴线作相对转动，因而有相对角位移，称为扭转角Twistingangle。同时，杆的纵向直线变为螺旋线（小变形时可近似为倾斜线）。变形情况:8/23/2021材料力学 用材力的方法只能解决等直圆杆（实心OR圆筒）的扭转问题和闭口薄壁直杆的自由扭转问题。8/23/2021材料力学 §3-3外力偶矩的计算CalculationofTorsionalLoads扭矩及扭矩图TorqueandTorqueFigure3.2.1CalculationofTorsionalLoads—Torsionalmoment一、手摇绞车之类:mc=Q×Rormc=P×b外力作用点到轴心的距离WD8/23/2021材料力学 §3-3外力偶矩的计算CalculationofTorsionalLoads扭矩及扭矩图TorqueandTorqueFigure二、机器传动轴:已知轴的转速为n(r·p·m);传递的功率P(kW=kN·m/s)则:单位时间所做的功为:W=P=me·(2pn/60)所以me=(30/π)·(N/n)=9.549N(kw)/n(r·p·m)---(3-4)注:主动轮上的外力偶矩（me）与轴的转向一致；被动轮上的外力偶矩（me）与轴的转向相反。注意到:1kW=1.36PS(马力),故有:8/23/2021材料力学 §3-3外力偶矩的计算CalculationofTorsionalLoads扭矩及扭矩图TorqueandTorqueFigureT(MT)可根据作用于圆轴上的外力偶矩mi由截面法求出;T(MT)的量纲:[力]·[长度]常用单位:N·m；kN·mT(MT)的正负规定:如图，按右手螺旋法则确定3.2.2扭矩Torque---扭矩轴的内力InternalforcesofTorsionshaft·扭矩图TorqueFigure一、扭矩Torque:外力偶矩作用于圆轴后，产生:扭转变形横截面的分布内力(剪应力)内力偶矩T(orMT,扭矩)8/23/2021材料力学 §3-3外力偶矩的计算CalculationofTorsionalLoads扭矩及扭矩图TorqueandTorqueFigure3.2.2Torque---InternalforcesofTorsionshaft·TorqueFigure二、扭矩图TorqueFigure按扭矩沿轴线的变化所作的内力图——扭矩图求Torque的基本方法:截面法——(注意用设正法)如图,n—n截面上(Ⅱ)部分(右侧)的扭矩大小和方向可由下面两种方法确定:(Ⅰ)①右侧部分自身平衡(外力偶矩m4,m5与T(MT)平衡),求出的T(MT)大小和方向作用于右侧部分的n—n截面。(Ⅱ)②左侧部分外力偶矩(m1,m2,m3)的代数和,求出的T(MT)大小和方向作用于右侧部分的n—n截面。8/23/2021材料力学 如果研究其右半段杆的平衡，则在同一横截面上所求得的扭矩在数值上与上面得到的相等但转向却相反(图c)。为使从两段杆所求得的同一横截面上的扭矩在正负号上一致,对扭矩的正负号应按杆的变形情况来规定。习惯上规定杆因扭转而使其纵向线在某一段内有变成右手螺旋线的趋势时，则该段杆横截面上的扭矩为正，反之为负。设一等直圆杆如图a所示，作用在杆上的外力偶矩分别为:m1=6m，m2=m，m3=2m，m4=3m。先求杆中间BC段中任一横截面I——I上的扭矩。用截面法将杆沿横截面I——I处假想地截分为二，并研究其左半段杆(图b)的平衡。由平衡方程得:§3-3外力偶矩的计算CalculationofTorsionalLoads扭矩及扭矩图TorqueandTorqueFigure此外，还可以将扭矩按右手螺旋法则用力偶矢来表示，并规定当力偶矢的指向离开截面时扭矩为正，反之为负。这两种对扭矩正负号的规定是一致的。按此规定，在图b或c中所示横截面I—I上的扭矩TI应为正号。扭矩Tl的转向如图b所示。这样，就可以使得按左段杆和右段杆的平衡条件所得到的同一截面上的扭矩在正负号上相一致。为了表明沿杆轴线各横截面上的扭矩的变化情况，从而确定最大扭矩及其所在横截面的位置，可仿照轴力图的作法(参见§2-2)绘制扭矩图。绘出图a所示的杆的扭矩图如图d。可见，最大扭矩Tmax在杆的左端一段内任一横截面上，其值为6m。8/23/2021材料力学 作扭矩图如图d。可见,最大扭矩Tmax在CA段内,其值为9.56kN·m。§3-3外力偶矩的计算CalculationofTorsionalLoads扭矩及扭矩图TorqueandTorqueFigure例题3-2:一传动轴如图a所示，其转速n=300r/min，主动轮输入的功率P1=500kW。若不计轴承摩擦所耗的功率，三个从动轮输出的功率分别为:P2=150kW、P3=150kW及P4=200kW。试作轴的扭矩图。解:首先按公式(3－4a)计算外力偶矩(图a)然后,由轴的计算简图(图b),用截面法计算各段轴内的扭矩,扭矩的正负号按前述的规定。先计算CA段内任一横截面II—II(图b)上的扭矩。沿横截面II—II将轴截开,并研究左边一段轴的平衡,假设TII为正值扭矩,由平衡方程结果为负号,说明TII应是负值扭矩(图c)。8/23/2021材料力学 实质:圆轴无轴向(伸缩)变形。圆轴受扭后，轴线无伸缩。即两横截面间的距离保持不变。§3-4等直圆杆的扭转TorsionofPrismaticShaft3.4.1受扭圆轴的应力和变形Stress&DeformationofShaftinTorsion.因为MT为绕轴线x的力偶矩，故只可能由横截面内的应力—剪应力t合成。由实验观察得圆轴扭转变形如图,其纵向直线(与杆轴x平行)变成相互平行的斜线。而圆周线的形状和尺寸均未变,圆周线之间的距离也未改变。故对圆轴扭转可作如下假设:⑴(刚)平面假设HypothesisofRigidCrossSection:圆轴受扭变形后,所有横截(平)面仍保持为平面,但绕杆轴线不同程度地转动了一个角度。(两相邻(dx)的横截面1—1,2—2产生相对转动角dφ)。实质:横截面无翘曲变形。⑵刚轴线假设RigidAxisHypothesis:以上两假设相当于把圆轴杆看成穿在刚性轴线上的无数圆薄片组成，两相邻圆薄片之间存在抗扭（转角）刚度。在受到扭矩作用时，每一圆薄片相对原来位置转动了一个角度。两相邻圆薄片之间存在相对扭转角dφ。8/23/2021材料力学 一、推导应力公式:§3-4等直圆杆的扭转TorsionofPrismaticShaft3.4.1受扭圆轴的应力和变形Stress&DeformationofShaftinTorsion.⑴变形的几何方面:从受扭圆轴中取dx微段来研究,如图:定义叫:单位长度扭转角Unitlength’sangleoftwist(inradians)则（a）随ρ线性变化，圆心处为0，圆周处为最大值。⑵物理方面:将本构关系代入(a)式，即可。当杆内应力时，有:……(b)⑶静力学方面:横截面上的切向内力元素对圆心的力矩合成扭矩MT(注意到为与半径垂直的周切线方向的剪应变，故):将(b)代入,得:(Gθ在积分的横截面内为常数，可提出来)故:8/23/2021材料力学 §3-4等直圆杆的扭转TorsionofPrismaticShaft3.4.1受扭圆轴的应力和变形Stress&DeformationofShaftinTorsion.2,圆环截面:…(3—5)其中:为由横截面形状和尺寸决定的几何常数，叫:极惯性矩PolarMomentofInertia。常用单位为:m4ormm4代入(b)式得:……(3—6)由(3—6)式知:①τρ只与MT、ρ、Ip有关，在静定问题中与所用材料无关。②τρ正比于其横截面上的扭矩MT；③τρ反比于其横截面的极惯性矩Ip；④τρ正比于欲求此应力的点到圆心的距离ρ；圆心处τ=0；圆周处τ最大；最大值为:tr的分布情况及方向如图所示:式中:叫抗扭截面模量(SectionModulusofTorsion)；常用单位为:m3ormm3。几何量Ip,Wt的计算:1,实心圆截面:8/23/2021材料力学 §3-4等直圆杆的扭转TorsionofPrismaticShaft3.4.1受扭圆轴的应力和变形Stress&DeformationofShaftinTorsion.二、扭转破坏现象分析PhenomenonAnalysesofTorsionalFailure如图，由剪应力互等定律，圆轴杆受扭时纵向存在与圆周向剪应力互等的剪应力。又由圆轴受扭时的变形假设，有:1,纵向线应变(两圆周线变形后间距不变)2,因横截面直径不变,故(ls圆周向)故又纯剪切单元体45和135两斜面上有sminorsmax,且由于各类材料的性质不同,抵抗剪切,抵抗拉伸变形的能力各异,故受扭破坏的常见现象有:a,沿橫截面抗剪切能力相对其它抗力较弱时，沿横截面被剪断（如软钢）b,b顺纹b横纹的木材，竹子等材料，受扭时沿径向纵截面剪开而破坏。c,铸铁等脆性材料的抗线伸长变形能力（lb）相对小于抗剪切能力（b）故受扭破坏时沿与杆轴线X成45°角的螺旋形曲面拉断。8/23/2021材料力学 §3-4等直圆杆的扭转TorsionofPrismaticShaft3.4.1受扭圆轴的应力和变形Stress&DeformationofShaftinTorsion.平面纯剪单元体任意斜截面上的应力Stressintheobliquesection·pureshearelement研究图示纯剪状态下与零应力面垂直的任意斜截面上的应力,设：e---f面面积dA，则:b---f面面积为dAsinae---b面面积为dAcosa即即由,得：a由x轴转向斜截面外法线方向n为逆时针转时为正，反之为负。t’(=-t)为y向剪应力的大小,由,得：讨论：1,2,(对应:,此时)8/23/2021材料力学 §3-4等直圆杆的扭转TorsionofPrismaticShaft3.4.1受扭圆轴的应力和变形Stress&DeformationofShaftinTorsion.扭转角j的单位为弧度(rad)。GIp叫等直圆杆的抗扭刚度三、受扭圆轴的变形DeformationofShaftinTorsion由:,得:对MT为常数的等直杆,有:8/23/2021材料力学 §3-4等直圆杆的扭转TorsionofPrismaticShaft3.4.2受扭圆轴的强度条件和刚度条件一、受扭圆轴的强度条件:同样可解三类问题。二、受扭圆轴的刚度条件:仍然可解三类问题。因为[q]常用单位为:°/m，故有:三、受扭圆轴的超静定问题:8/23/2021材料力学 扭转变形能如图，故meme可见当mc从0Mc时，此圆柱外力作功为:弹性阶段变形能U=T，故:8/23/2021材料力学 结论适用条件:①R>>d(可忽略曲率影响,式中d为:弹簧直径)；②小间距（密圈）使:③忽略剪力(Q=P)对弹簧变形的影响；④线弹性范围:ex,密圈螺旋弹簧(close—coiledhelicalspring)结论:故:弹簧刚度8/23/2021材料力学 §4—5非圆截面杆纯扭转的概念thecomceptsofNoncircularmembersinPureTorsion注:①我们只讨论纯扭转问题；②实体截面杆由于约束扭转所引起的附加正应力一般很小，可忽略不计；但薄壁杆件约束扭转时会产生不能忽略的附加正应力。非圆截面杆扭转的一大特点-----有翘曲(warp)产生。故圆轴杆扭转的结论不能应用于它。解决非圆截面杆扭转问题一般需用弹性理论方法or实验方法(如:薄膜比拟MembraneAnalogy)。非圆截面杆扭转常分为自由扭转（PureTorsion、FreeTorsion）和约束扭转（ConstrainedTorsion、RestrainedTorsion）两种。PureTorsion:任一截面的翘曲不受端部约束，能自由翘曲，且两相邻横截面的翘曲程度完全相同（此时任一横截面上只有τ而无s）。RestrainedTorsion：截面的翘曲受端部约束限制，不能自由翘曲or扭矩MT随轴线x变化，使两相邻横截面的翘曲程度不同（此时任一横截面上一般不但有τ，还有s产生）。8/23/2021材料力学 矩形截面杆Rectangularsectionbarτ在横截面上的分布，见图，由弹性力学分析可得截面最大剪应力:……（4—11）发生在长边中点相距L的两截面的相对扭转角:……（4—12）其中:MT—杆横截面上的扭矩；系数；可由查表确定。各角点上τ=0（由剪应力互等定理可证明之）（且当m>10时，有:α=β=m/3）8/23/2021材料力学 其分布见图狭长矩形截面杆ThinRectangularSection(长边h,短边t)由表可知当时，有:且8/23/2021材料力学 由刚周边假设:杆扭转后，横截面周线虽然在杆表面上变成曲线，但在其变形前的平面上的投影形状仍保持不变(即就横截面的投影来说，它在杆扭转时将作刚性转动)。可得:开口薄壁截面Thin-WalledOpenSections参见图，开口薄壁截面可视为由若干狭长矩形组合而成。故剪应力仍沿周边形成剪应力流。而τ的方向由(τdA)组成的力偶转向与MT一致来确定。由可得:(i=1,……,n)又因为:故得:因此:注意到:故整个截面的最大剪应力:发生在厚度最大的狭长子矩形的长边上相距l的两截面之间的扭转角:8/23/2021材料力学 §3-7等直非圆杆在自由扭转时的应力和变形8/23/2021材料力学 §3-7等直非圆杆在自由扭转时的应力和变形8/23/2021材料力学 8/23/2021材料力学 8/23/2021材料力学 作业:3-1、3-3、3-18、3-25、3-31、3-33、3-358/23/2021材料力学