机械系统动力学三级项目报告材料

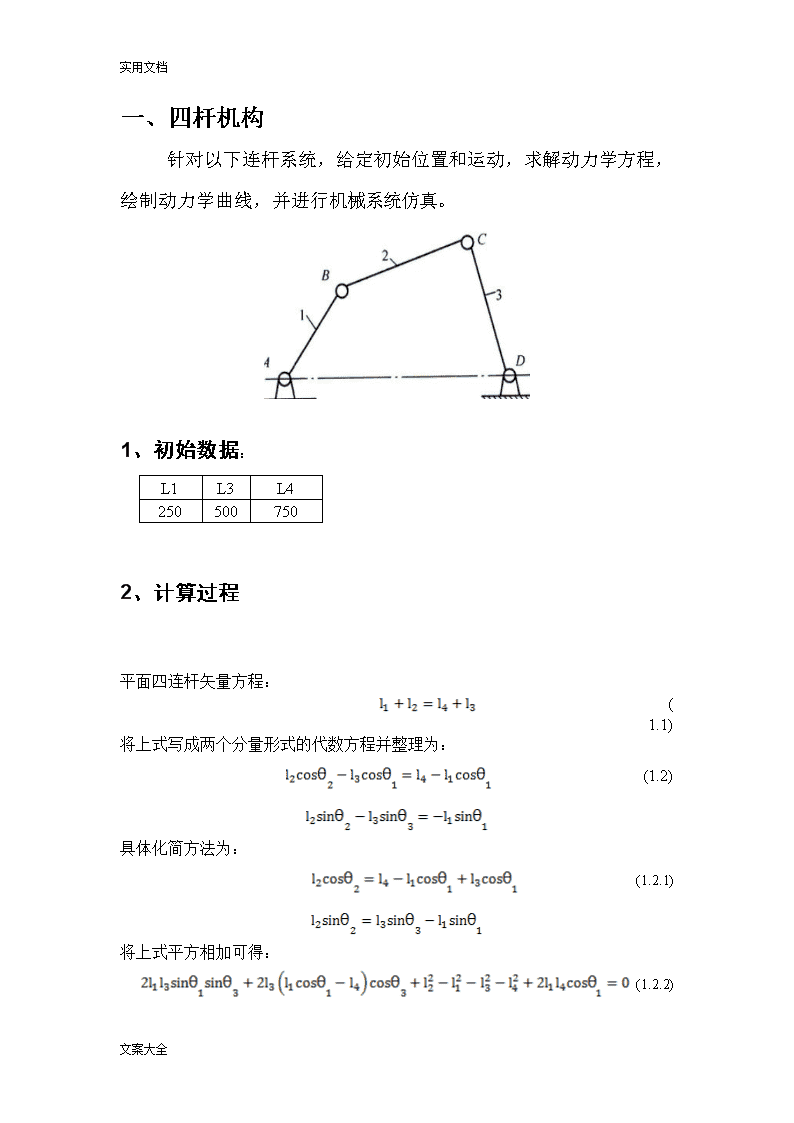
'实用文档机械系统动力学三级项目报告指导老师：胡波小组成员：班级：机电1班完成时间：2015年7月4日文案大全 实用文档目录一、四杆机构11、初始数据22、计算过程23、运动仿真53.1SolidWorks运动仿真53.2simulink仿真63.3MATLAB编程7二、单自由度101、初始数据102、自由振动103、受迫振动102.1无阻尼102.2小阻尼振动132.3临界阻尼152.4大阻尼173、受迫振动193.1无阻尼193.2有阻尼213.2Solidworks运动仿真21三、两自由度振动231、自由振动242、受迫振动26文案大全 实用文档一、四杆机构针对以下连杆系统，给定初始位置和运动，求解动力学方程，绘制动力学曲线，并进行机械系统仿真。L1L3L42505007501、初始数据：2、计算过程平面四连杆矢量方程：(1.1)将上式写成两个分量形式的代数方程并整理为：(1.2)具体化简方法为：(1.2.1)将上式平方相加可得：(1.2.2)文案大全 实用文档令：(1.2.3)则有：(1.2.4)解之可得位置角：(1.3)同理为求，应消去将式(1.2)改写为：(1.4)整理后可得：(1.5)其中：D=2l1l2sinθ1E=2l2（l1cosθ1-l4）F=l12+l22+l42-l32-2l1l4cosθ1解得：θ2=2arctan[(D±）/(E-F)](1.6)杆r2上任意一点的位置坐标为：lx=l1cosθ1+l2＇cosθ2ly=l1sinθ1+l2＇sinθ2（1.7）2、平面四连杆的速度、加速度分析式（1.2）对时间求导，可得：-l2ω2sinθ2+l3ω3sinθ3=l1ω1sinθ1l2ω2cosθ2-l3ω3cosθ3=-l1ω1cosθ1（1.8）解之得r2、r3的角速度ω2、ω3为：ω3=ω1=ω1文案大全 实用文档ω2=ω1=ω2（1.9）式（1.7）对时间求导，可得r2杆上任意一点的速度方程为：Vlx=-l1ω1cosθ1-l2＇ω2sinθ2Vly=l1ω1sinθ1-l2＇ω2cosθ2（1.10）式（1.8）对时间求导，可得：-l2ε2sinθ2+l3ε3sinθ3=l2cosθ2-l3cosθ3+l1cosθ1l2ε2cosθ2-l3ε3cosθ3=l2sinθ2-l3sinθ3+l1sinθ1（1.11）解之得杆r2、r3的角加速度为：ε3=ε2=（1.12）式（1.10）对时间求导，可得杆r2上任意一点的线性加速度为：alx=-l1ε1sinθ1-l1cosθ1-l2＇ε2sinθ2-l2＇cosθ2aly=l1ε1cosθ1-l1sinθ1+l2＇ε2cosθ2-l2＇sinθ2（1.13）2、平面四连杆的动力学分析设Go表示BC杆的重力，（FmTm）表示BC杆的广义惯性力和惯性矩，Gmi表示AB、CD，（FmiTmi）表示AB、CD杆的广义惯性力和惯性矩。Fm=-moa，Tm=-J0ε0Gm=mog，Fmi=-mpiapi，Tmi=-JpiεiGmi=mpig，J0=mo+mod2J1=moJ3=m3根据虚功原理将各分支受到的惯性力/矩和重力，全部映射到动平台上去，[FT]T表示BC杆受到的总的动态负载。[FsTs]T表示BC杆所受的静态负载，在这里，用速度代替虚功原理中的虚位移。文案大全 实用文档Vp1+V+=0（1.14）由于杆AB为纯转动，广义力和广义速度只有一项为非零，容易得到驱动力矩为：T=-V+3、运动仿真3.1SolidWorks运动仿真3.1.1三维建模：3.1.2仿真曲线如下：文案大全 实用文档3.2simulink仿真出图如下：文案大全 实用文档3.3MATLAB编程程序如下：l1=250;l2=510;l3=500;l4=750;l1=l1/1000;l2=l2/1000;l3=l3/1000;l4=l4/1000;%%th0=60;%%杆1初始位置th=deg2rad(th0);m1=0.05221;m2=0.10421;m3=0.10221;w1=pi/3;%%初始速度w1=(2*pi*12)/60vr=[w1];aw1=0;%%初始角加速度l2_1=l2/2;t=1;g=[0;0];fortime=0:0.05:5th1=th+w1*time;A=2*l1*l3*sin(th1);B=2*l3*(l1*cos(th1)-l4);C=l2^2-l1^2-l3^2-l4^2+2*l1*l4*cos(th1);th3_2=2*atan((A+(A^2+B^2-C^2)^(1/2))/(B-C));文案大全 实用文档th3_1=2*atan((A-(A^2+B^2-C^2)^(1/2))/(B-C));D=2*l1*l2*sin(th1);E=2*l2*(l1*cos(th1)-l4);F=l2^2+l1^2-l3^2+l4^2-2*l1*l4*cos(th1);th2_2=2*atan((D+(D^2+E^2-F^2)^(1/2))/(E-F));th2_1=2*atan((D-(D^2+E^2-F^2)^(1/2))/(E-F));th2=th2_1;th3=th3_1;lx=l1*cos(th1)+l2_1*cos(th2);ly=l1*sin(th1)+l2_1*sin(th2);J1(t)=(1/12)*m1*l1^2*(10^(-6));J3(t)=(1/12)*m3*l3^2*(10^(-6));J2(t)=(1/12)*m2*l2^2*(10^(-6));w2(t)=w1*(l1/l2)*((sin(th1)*cos(th3)-cos(th1)*sin(th3))/(sin(th3)*cos(th2)-cos(th3)*sin(th2)));w3(t)=w1*(l1/l3)*((sin(th1)*cos(th2)-cos(th1)*sin(th2))/(sin(th3)*cos(th2)-cos(th3)*sin(th2)));aw2(t)=(l2*w2(t)^2*cos(th3-th2)-l3*w3(t)^2+l1*w1^2*cos(th3-th1))/(l2*(sin(th3)*cos(th2)-cos(th3)*sin(th2)));aw3(t)=(l1*w1^2*cos(th1-th2)+l2*w2(t)^2-l3*w3(t)^2*cos(th3_1-th2))/(l3*(sin(th3)*cos(th2)-cos(th3)*sin(th2)));vlx(t)=-l1*w1*sin(th1)-l2_1*w2(t)*sin(th2);vly(t)=l1*w1*cos(th1)+l2_1*w2(t)*cos(th2);alx(t)=-l1*aw1*sin(th1)-l1*w1^2*cos(th1)-l2_1*aw2(t)*sin(th2)-l2_1*w2(t)^2*cos(th2);aly(t)=l1*aw1*cos(th1)-l1*w1^2*sin(th1)+l2_1*aw2(t)*cos(th2)-l2_1*w2(t)^2*sin(th2);v1(:,t)=[-sin(th1);cos(th1)]*(l1/2)*w1;a1(:,t)=[-w1^2*cos(th1)-aw1*sin(th1);-sin(th1)*w1^2+cos(th1)*aw1]*(l1/2);v0(:,t)=[vlx(t);vly(t)];w0=[w2(t)];a0(:,t)=[alx(t);aly(t)];aw0=[aw2(t)];v3(:,t)=[-sin(th3);cos(th3)]*(l3/2)*w3(t);文案大全 实用文档a3(:,t)=[-w3(t)^2*cos(th3)-aw3(t)*sin(th3);-sin(th3)*w3(t)^2+cos(th3)*aw3(t)]*(l3/2);G2=m2*g;f2=-m2*a0(:,t);n2=-J2(t)*aw2(t);G1=m1*g;f1=-m1*a1(:,t);n1=-J1(t)*aw1;G3=m3*g;f3=-m3*a3(:,t);n3=-J3(t)*aw3(t);M(t)=-([f2"+G2"n2"]*[v0(:,t);w0]+[f1"+G1"n1"]*[v1(:,t);w1]+[f3"+G3"n3"]*[v3(:,t);w3(t)])/vr;t=t+1;endtime=0:0.05:5;plot(time,M);所得曲线如下：    文案大全 实用文档二、单自由度给定单自由度系统参数，对单自由度无阻尼和有阻尼自振动系统进行计算，分别绘制无阻尼、小阻尼、临界阻尼和大阻尼响应曲线，并进行仿真；物体上施加一简谐力，绘制无阻尼和有阻尼状态下的受迫振动曲线，并进行仿真。要求：仿真使用solidwoks和matlab/simulink同时进行。1、初始数据刚度系数（N/m）滑块尺寸（mm）15602、自由振动曲线2.1无阻尼2.1.1SolidWorks仿真文案大全 实用文档2.1.2simulink仿真：出图如下：文案大全 实用文档2.1.3MATLAB编程：单自由度系统的运动方程如下：，其中；由初始条件可计算出A和θ。程序如下：m=1.6632;k=15;wn=sqrt(k/m);x0=10;v0=0;A=sqrt(x0^2+v0^2/wn^2);a=atan(wn*x0/v0);t=0:0.02:5;x=A*sin(wn*t+a);Plot(t,x)所得曲线如下：文案大全 实用文档2.2小阻尼振动2.2.1SolidWorks仿真2.2.2simulink仿真：文案大全 实用文档2.2.3MATLAB编程有阻尼情况下，滑块的运动方程如下：由初始条件可求得A和θ。程序如下：m=1.6632;k=15;wn=sqrt(k/m);c=1.5;n=c/(2*m);x0=10;v0=0;A=sqrt(x0^2+(v0+n*x0)^2/(wn^2-n^2));a=atan(x0*sqrt(wn^2-n^2)/(v0+n*x0));t=0:0.02:5;x=A.*(exp(-n*t)).*sin(wn*t+a);Plot(t,x);所得曲线如下：文案大全 实用文档2.3临界阻尼2.3.1SolidWorks运动仿真2.3.2MATLAB编程编程如下：m=1.6632;k=15;wn=sqrt(k/m);n=wn;x0=10;v0=0;c1=x0;c2=v0+n*c1;t=0:0.02:5;x=exp(-n*t).*(c1+c2*t);Plot(t,x);所得曲线如下：文案大全 实用文档2.3.3simulink仿真：文案大全 实用文档2.4大阻尼2.4.1SolidWorks运动仿真2.4.2MATLAB编程编程如下：m=1.6632;k=15;wn=sqrt(k/m);n=5;[c1,c2]=solve("-c1-c2=10","1.0023*c1+8.9977*c2=0","c1","c2");t=0:0.01:5;x1=(-c1*exp(-n*t+t*sqrt(n^2-wn^2)));x2=(-c2*exp(-n*t+t*sqrt(n^2-wn^2)));x=x1+x2;Plot(t,x)；所得曲线如下：文案大全 实用文档2.4.3simulink仿真：文案大全 实用文档3、受迫振动3.1无阻尼3.1.1Soloidworks运动仿真3.1.2MATLAB编程运动方程如下：由初始条件可求得A和θ。程序如下：m=1.6632;k=15;H=1;wn=sqrt(k/m);文案大全 实用文档w=2*pi;x0=0;v0=0;h=H/m;b=h/(wn^2-w^2);A=sqrt(x0^2+(v0-b*w)^2/wn^2);a=atan(wn*x0/(v0-b*w));t=0:0.005:5;x=A*sin(wn*t+a)+b*sin(2*pi*t);Plot(t,x)；所得曲线如下：文案大全 实用文档3.1.3simulink仿真：3.2有阻尼3.2.1Soloidworks运动仿真文案大全 实用文档3.2.2simulink仿真：3.3.3MATLAB编程运动方程如下：由初始条件可求得A和θ。程序如下：m=1.6632;k=15;H=1;wn=sqrt(k/m);w=2*pi;h=H/m;c=7;n=c/(2*m);wd=sqrt(wn^2-n^2);b=h/(sqrt((wn^2-w^2)^2+4*n^2*w^2));o=atan(2*n*w/(wn^2-w^2));y=sin(o);y1=cos(o);A=-sqrt((n*b*y-b*w*y1)^2/wd^2+b^2*y^2);a=atan(wd*y/(n*y-w*y1));文案大全 实用文档t=0:0.05:5;x=-(A*(exp(-n*t)).*sin(wd*t+a)+b*sin(w*t-o));Plot(t,x);所得曲线如下：三、两自由度振动给定两自由度系统参数，对两自由度自由振动系统进行计算，绘制响应曲线，并进行仿真；对其中末端物体上施加一简谐力，绘制受迫振动曲线，并进行仿真。文案大全 实用文档要求：编程计算软件不限，只要绘出曲线即可。仿真使用solidwoks和matlab/simulink两种软件同时进行,计算结果和仿真结果一致；1、自由振动1.1Soloidworks运动仿真1.2simulink仿真出图如下：文案大全 实用文档1.3MATLAB编程运动方程如下：由初始条件确定编程如下：m=1.6632;k=15;q10=0;q20=10;p1=sqrt((3-sqrt(5))*k/(2*m));p2=sqrt((3+sqrt(5))*k/(2*m));u1=(p1^2*m-2*k)/(-k);文案大全 实用文档u2=(p2^2*m-2*k)/(-k);X12=(1/(u2-u1))*sqrt((u2*q10-q20)^2);X11=(1/(u1-u2))*sqrt((u1*q10-q20)^2);a1=-pi/2;a2=-pi/2;t=0:0.01:5;x=-(u1*X11*sin(p1*t+a1)+u2*X12*sin(p2*t+a2));Plot(t,x)2、受迫振动2.1Solidworks运动仿真文案大全 实用文档2.2simulink仿真2.3MATLAB编程运动方程如下：文案大全 实用文档由初始条件确定编程如下：m=1.6632;k=15;F0=0.5;w=2*pi;q10=0;q20=0;X1=k*F0/((k-m*w^2)*(k-m*w^2)-k^2);X2=(2*k-m*w^2)*F0/((2*k-m*w^2)*(k-m*w^2)-k^2);p1=sqrt((3-sqrt(5))*k/(2*m));p2=sqrt((3+sqrt(5))*k/(2*m));u1=(p1^2*m-2*k)/(-k);u2=(p2^2*m-2*k)/(-k);X11=(1/(u1-u2))*sqrt((u2*X1*w-w*X2)^2/p1^2);X12=(1/(u2-u1))*sqrt((u1*X1*w-w*X2)^2/p2^2);a1=0;a2=0;t=0:0.01:5;x=u1*X11*sin(p1*t+a1)+u2*X12*sin(p2*t+a2)+X2*sin(w*t);Plot(t,x);出图如下：文案大全'