化学分析中测量不确定度的评定方法概述

'化学分析中测量不确定度的评定方法概述化学分析是检验检疫工作中使用频率最高的实验方法之一。对化学分析中测量不确定度的评定已进行过广泛的论述。这里，用较为系统的观点对化学分析中测量不确定度评定的一般方法进行讨论，以便为实际工作提供参考。在总的范围内，化学分析是相对于物理测量等其他测量方法而言的。而在测量的化学方法中，化学分析是相对于仪器分析而言的，这里所涉及的化学分析是指后一种情况。它包括了很多经典的分析方法，如重量法、容量法。同时，为了扩展化学分析方法的分析范围和提高分析水平，可能还包括了某些复杂的样品处理过程等方面。在不确定度的评定中，化学分析中许多通用的要素的处理方法可以是一致的，本文大体归纳了这些要素，并将它们作为测量不确定度的分量分别考察，探讨各分量不确定度的评定方法及这些分量之间的相互关系。1．化学分析中的通用分量及其不确定度的评定方法1.1化学分析中的测量方法和被测量重量法和容量法是化学分析中的两类基本方法，根据被测量的不同，会采用不同的分析原理或条件，如容量法中有滴定分析、气体容量分析等方法。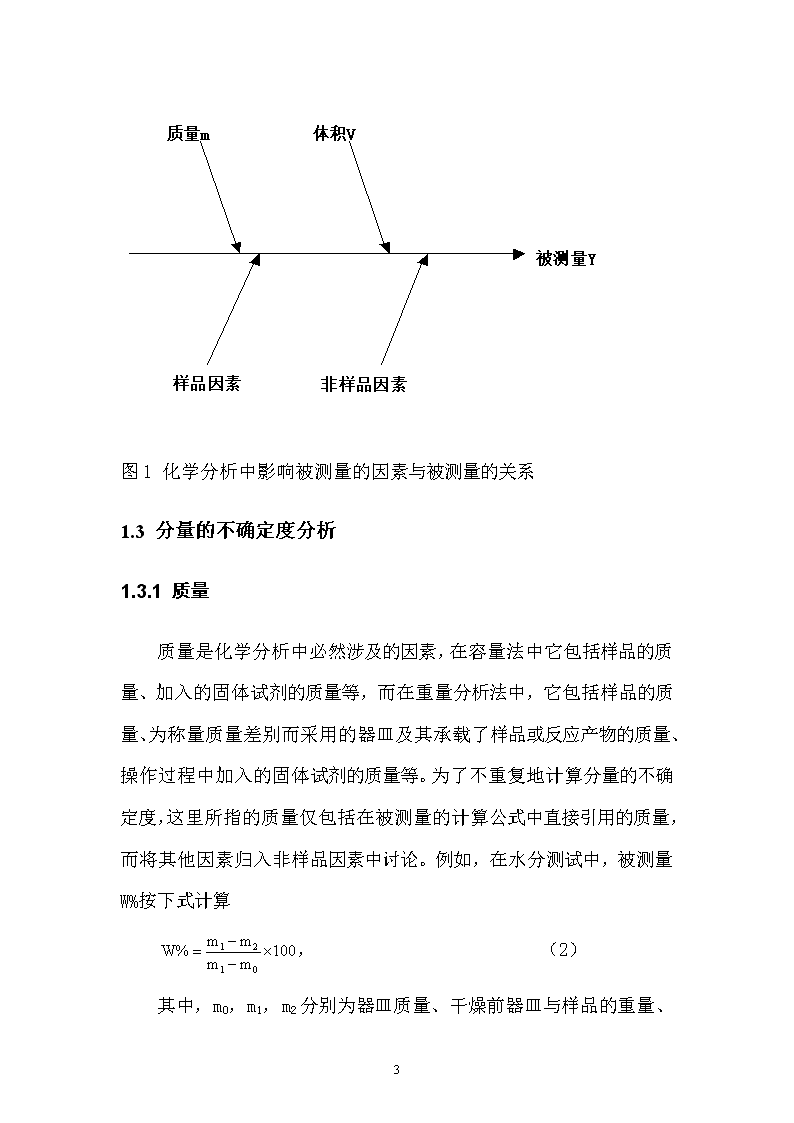23 但是，化学分析方法具有共同的特点，其被测量都是样品中某特定元素的含量或纯度。对于含量分析来说，其最终目的是得到该元素的含量值，一般采用直接测量和计算的结果；而纯度是将相关或规定的元素含量扣除后的结果。无论最终结果使用那种单位或形式表示，都可以表示为式1的形式：，（1）其中，Xi为对被测量Y有影响的输入量。这些输入量可以是直接测量得到的，也可以是从其他测量结果导入的。1.2化学分析中涉及的通用分量及其与被测量的关系大多数情况下，化学分析方法中采用手工方法，对化学分析结果的不确定度产生影响的因素很多，大体可以分为质量、体积、样品因素和非样品因素等。质量因素和样品因素存在于所有化学分析中，而容量分析中必然涉及体积因素。由于测量原理的不完善及测量过程的不同，在化学分析中还可能存在非样品因素。只要能够明确地给出被测量与对其不确定度有贡献的分量之间的关系（如式1），则这些分量怎样分组以及这些分量如何进一步分解为下一级分量并不影响不确定度的评定。因此，可以将这些通用分量与被测量的关系采用图1所示的因果图表示。23 图1化学分析中影响被测量的因素与被测量的关系1.3分量的不确定度分析1.3.1质量质量是化学分析中必然涉及的因素，在容量法中它包括样品的质量、加入的固体试剂的质量等，而在重量分析法中，它包括样品的质量、为称量质量差别而采用的器皿及其承载了样品或反应产物的质量、操作过程中加入的固体试剂的质量等。为了不重复地计算分量的不确定度，这里所指的质量仅包括在被测量的计算公式中直接引用的质量，而将其他因素归入非样品因素中讨论。例如，在水分测试中，被测量W%按下式计算，（2）其中，m0，m1，m223 分别为器皿质量、干燥前器皿与样品的重量、干燥后器皿与样品的重量。这时所考察的质量分量仅包括m0，m1，m2。化学分析中测量质量的唯一方法是使用天平，影响质量测量结果的因素包括天平的校准、称量操作、环境等。操作在天平上获取的质量测量结果因其在计算被测量时的作用不同而具有不同的测量不确定度贡献。a质量的称量应使用两次观测的结果，实际上，化学分析中的大部分质量是两次观测的结果，因此有毛重和皮重的不确定度的合成问题。而在水分测试这样简单的实验中，情况却有所变化，我们在公式中使用的独立量是m0，m1，m2，而m1和m2就不存在皮重的问题。E，当在被测量中只关心样品的质量，而如何称量出这个质量并无影响时（在容量分析和大多数重量分析中），必须在天平上读取两次质量，一次是皮重，另一次是毛重。所得到的样品质量ms实际上可以表示为，其中mG和m0分别为皮重和毛重。因此，在考察这种质量的不确定度时，应将有关的不确定度计算两次。即b）在另一种情况下，被测量的计算中引入单次称量值，例如式（2）所表示的水分测量的情况。这时，应考虑称量操作是连续完成的还是间断的。在上面的水分测量的例子中，器皿的质量m0和干燥前器皿与样品的质量m1是连续称量的，其中m023 是两次观测的结果，而m1则是一次观测的结果。而同样包含器皿质量的干燥后质量m2与器皿质量m0并不是连续称量的，所以m2也是两次观测的结果。校准由于天平是法定计量的器具，因而其校准过程使用的测量标准和比较方法所引入的不确定度相对于称量的质量值来说可以忽略。因此，天平校准的不确定度的主要来源是天平示值的不确定度。天平示值的不确定度可以从天平的检定证书中获得，某些检定证书中给出了示值的扩展不确定度值，可以将其转变为标准不确定度直接使用。例如，检定证书中给出在置信概率95%时的天平称量的不确定度为±0.1mg，则可直接按正态分布换算成标准不确定度0.1/1.96=0.052mg。而另一些证书中仅给出了合格评定，这时应参照有关检定标准或规程确定其标准不确定度。例如对于最大称量为100g，分度值为0.1mg的天平来说，其准确度级别为4级，其最大允许误差为±e，即±0.1mg。这时采用均匀分布处理,即天平称量的标准不确定度为0.1/=0.058mg。有时天平的生产厂也会建议采取均匀分布处理天平的示值的不确定度问题。在校准方面，天平在整个量程范围内的系统偏移一般很小而被忽略。化学分析一般是在同一台天平上进行称量，因此天平灵敏度的影响可以忽略。环境23 能够影响称量的环境因素很多，例如温度、湿度、振动、气流、环境气氛及其压力等。这些因素对称量的影响程度是不同的，有时还会随着具体的实验方法而不同。例如，在使用热称量方法测定铁矿石水分时，温度的影响就不得不在不确定度的评定中加以考虑。如果在湿度较大的气氛中称量已完全干燥的样品或试剂时，则这些样品或试剂就会吸收一些水分，从而带来质量的不确定度。一般情况下，称量所得出的质量是空气中的质量，因此不需进行空气浮力校正。称量所处环境气氛的压力一般不会对称量的质量产生影响，因此也不必考虑。称量时应保证在一定的振动和气流水平中进行，正常的气流和振动水平所产生的不确定度已包含在天平校准的不确定度中，不需重复计算，而过分的气流或振动则是操作上的失误，不属于测量不确定度的范畴。称量的变动性变动性是称量中的随机性。也就是说，称量同一质量的物质可能产生不同的示值。变动性可以采用多次称量同一物质的方法来求得，其质量的标准偏差就是其标准不确定度。当实验方法中给出了方法的重复性或再现性限值时，可以将称量的变动性并入重复性或再现性中考虑，在后面的论述中将讨论这一问题。在一般的化学分析中，仅考虑天平校准这一分量，将称量的变动性划归重复性或再现性中，忽略其他因素的影响可能是最简单实用的处理方法。小结23 从以上的讨论可以得到以下结论：1．质量的不确定度是由影响质量的各个因素合成的；2．天平校准和称量的变动性所带来的不确定度一般会成为质量不确定度的主要来源；3．称量操作的不同影响质量不确定度的合成；4．特殊的称量程序可能会要求考虑环境等其他因素的影响；5．称量变动性所产生的不确定度有时可以归并到实验方法的重复性或再现性中。由此，我们可以细化质量分量的因果图23 1.3.2体积体积是容量分析中必然涉及的因素。化学分析中定量使用的体积包括从量入式或量出式器具得出的体积（这种器具可能使用不同的材料制成，如玻璃、塑料或金属）、由质量和密度之比值换算出的体积和由规则或不规则的外部或内部尺寸计算得出的体积等。后两种体积是由质量、密度或长度决定的，它们的不确定度的评定应由其分量的不确定度合成得出。质量不确定度的评定方法已讨论过，密度的不确定度由另一些实验或公认的基本数据导出，长度的不确定度取决于所使用的测量长度的器具等因素，这些都不在本文的讨论范围内。下面仅就直接测量的体积，即从量器得出的体积作出简要的说明。23 影响由量器得出的体积的因素包括量器的校准、使用和环境等方面。校准量器的校准能够给出在校准条件下的量器体积的不确定度，有时在检定证书中直接给出了体积的扩展不确定度及其包含因子的信息，这时可直接换算成标准不确定度使用。但在大多数情况下，特别是在我国现行的计量体系中，仅给出合格评定，这时要依照相关的标准或规程用最大允许差值按均匀分布或三角分布计算。例如，所使用的25mL移液管的最大允许差为±0.03mL，则其标准不确定度为0.03/=0.012mL。当使用正确的自行校准方法校准量器时，其标准不确定度应从校准的过程中导出，例如，用称重的方法校准容量瓶时，可以从质量等分量合成容量瓶体积的标准不确定度。使用量器的使用会带来不确定度主要来自于读数的重复性或再现性。读数的重复性或再现性可以通过试验求得，例如进行多次读数求得标准偏差，或将这部分的不确定度归并到实验方法的重复性或再现性中。环境23 量器的使用环境与校准环境的差别会产生不确定度。量器的温度、量器内部的压力、清洁程度等。量器使用温度与校准温度的差别是引入体积不确定度的重要原因，温度的变化会导致量器体积的膨胀或紧缩，不同材质量器的体积膨胀系数不同，查阅GB/T12810-91标准得知，用于制作玻璃量器的材料的体热膨胀系数分别为：石英1.6×10-6K-1；硼硅酸盐1.0×10-5K-1；钠钙玻璃2.5×10-5K-1。在通常的容量分析中使用硼硅酸盐玻璃较多，按照均匀分布可以求出温度差别引起的体积不确定度。量器内部的压力对于气体的分析非常重要，例如使用定量进样阀采取一定体积的气体用于分析，则应注意实际使用的压力与校准时使用的压力的差别，这种差别引入的不确定度的计算方法类似于温度的情况。量器内部和外部的清洁程度可能会影响测量结果，应按照实验方法和量器使用的基本要求清洁量器，由量器的不清洁带来的体积或最终测量结果的不确定度是无法估计的，也是实际工作中应避免的，同样不属于不确定度的讨论范畴。小结从以上论述可知，体积不确定度的评定应考虑以下四个方面：1．量器具校准时给出的体积不确定度；2．体积读数的重复性或再现性；3．读出体积的读数次数；4．温度、压力等环境因素的改变所引入的不确定度。由此，我们可以得到体积分量的不确定度因果图23 1.3.3样品的非均匀性、取样和制样样品的非均匀性可能会导致测量结果的巨大差异。对于标准方法和经过验证的成熟方法来说，样品的非均匀性只是一种随机效应。这种随机效应导致的不确定度可以采用采用多次测定同一样品的某一被测量的方法得出，但更好的处理方法是将其并入方法的重复性或再现性中。取样和制样过程对化学分析结果也会产生巨大的影响，一般认为，取样和制样过程的不确定度远远大于化学分析的不确定度。取样和制样直接影响测量数据的代表性和测试样品的均匀性。但是这已超出了本文所讨论的范围。23 1.3.4测试过程中的因素这些因素包括关键的测试步骤，如样品的前处理、试剂或溶剂的加入、测试所依据的化学反应等。测试过程所引入的不确定度对于不同的测试过程是不同的，对这种不确定度的评定应考虑具体的测试过程，既要注意所有的测试步骤都存在引入不确定度的可能，也要注意不能重复计算。在化学分析中，有几类问题具有明显的共性：前处理问题在许多化学分析实践中，前处理是必要的测试步骤，如溶解、萃取、熔融、消化等。这些步骤的目的是将与被测量有关的样品中的某些成分转化成可测量的形式，包括进行富积操作以达到测量的鉴别力阈方面的要求，即待测组分的浓度达到测量的最低要求。前处理过程中涉及到反应的完全程度、富积的比率、待测组分的损失等，通常的方法是在被测量的计算中引入一个系数与计算被测量的式子相乘，将这一系数称为某某校正因子。将校正因子作为被测量不确定度的一个独立分量单独评定。可以采用加标回收等方法确定校正因子的值及其不确定度。23 当回收试验的成本可能较高，或找不到适当的加入标准而使回收实验无法进行时，可以采用B类评定方法，借鉴已有的研究成果，如标准方法的编制说明、文献中的数据等确定校正因子的不确定度。对于成熟的经典方法来说，校正因子接近于1，且其不确定度很小，可以忽略。不完全反应和不定量反应问题测试过程中的不完全反应和不定量反应是经常遇到的问题，例如在络合滴定中生成多种络合物的情况、许多反应产生副反应的情况。这时，可以参照上述前处理问题的解决方法解决。等量点偏移问题等量点的偏移包括两个方面，一是在弱酸弱碱滴定中，由于所使用的指示剂变色点与等量点不一致而导致的系统偏差，二是标准溶液浓度的校准过程中所使用的指示剂等条件与样品测试时所使用的不一致。同样可以采取加入校正因子的方法解决这一问题。在许多经典的化学分析方法中，由于等量点偏移导致的不确定度对总不确定度的贡献很小，因此不需考虑。上述三类问题中所使用的校正因子有时是相关的量，例如等量点偏移经常包含于为前处理或不完全（定量）反应所设计的加标回收试验中，所以在实际评定中不应重复计算这些分量。恒重问题恒重问题是重量法中经常遇到的，恒重一般是指两次称量的差值不超过某个限值。处理时可采用矩形分布，即将这个限值除以23 得到标准不确定度。恒重问题仅影响所测定的某个质量，因此应将这一影响加入到质量分量中。干扰问题干扰问题也是化学分析中经常遇到的问题，如络合滴定测定某个金属元素的含量时，另一些元素与标准溶液也存在反应的可能，而使测得的含量值偏高。经常采用的方法是加入一定量的掩蔽剂或沉淀剂等，或在样品的前处理阶段消除这种干扰。但是，仍有一些干扰是无法完全消除的，因而采用了空白试验的做法，实际上是给测定的结果加入了一个修正值。空白试验分为两种情况，一是从被测量中扣除空白值，二是反滴定的情况。第一种情况下，一般所得到的空白值较低，有时甚至比估计的不确定度还要小，这时可以不必考虑用空白进行修正，即使进行修正也可忽略空白的不确定度。扣除的空白的不确定度与相同量的不确定度的影响因素相似，因此可以用相似的方法进行评定。反滴定时使用的空白值是不能忽略的，它不仅在被测量的计算中占有重要地位，而且还会涉及定量过量加入的标准溶液体积的重复性。因此，在反滴定方法中，测量不确定度的评定不仅要考虑直接用于计算的量的影响，而且还要考虑没有直接参加计算的量的影响。23 1.3.5实验方法的重复性和再现性许多国家标准中给出的重复性和再现性实际上是该实验的重复性或再现性限值。近年来标准中所给出的重复性限值r或再现性限值R一般是按照GB/T11792的规定通过实验室间精密度试验得出的。它给出的形式可能是单一的数值，或依样品特性值水平而划分的分段函数，或者以它们对样品特性值大小的连续函数表示。在给出数值或函数的同时也给出了置信概率。23 在某些近期未做修订的标准或方法中，并未采用r或R的形式表示重复性或再现性，经常出现的词汇是允许差，最大允许差，容许误差，平行误差等。这些词汇产生于不同的历史背景和行业，其中的一些概念是不完善的。关于这些词汇与重复性限或再现性限的关系，可参阅有关标准和专著。从前5节的论述中可以发现，测量的各个方面均包含了随机效应所导致的不确定度，这些随机效应可以归并到一起，在重复性或再现性条件下与实验方法的r或R值存在着必然的联系。实际上，通过实验室间协同试验所得出的r和R值就是该实验方法中随机效应导致的总不确定度的量度，它们是在一定的置信概率下给出的随机效应的扩展不确定度，包含了测量的所有方面的随机效应。除非特殊说明，可以用r/2.83或R/2.83来表示随机效应导致的标准不确定度，并在其他分量中不考虑随机效应。如果将实验方法中所有的随机效应考虑成一个分量，则有下面的因果图：23 1.3.6外部数据被测量计算中所使用的外部数据包括常数和由其他实验得出并导入的量值。常数分为两种，一种是单位换算使用的数字常数，例如从mg换算成g需要1000这个常数；另一种是手册、技术说明、资料中给出的参考常数。前一种常数的不确定度显然是可以忽略的，后一种情况则需进行不确定度的评定，如分子量的不确定度的评定等。23 由其他实验得出的数据本身可能具有可观的不确定度，例如容量分析中所使用的基准试剂纯度、标准溶液浓度、仪器设备校准试验得出的测量值的不确定度等。仪器设备校准方面的问题一般归并到各分量中评定。在化学分析中经常使用的外部数据是分子量、基准试剂纯度和标准物质的标准值。依据IUPAC最新公布的相对原子量表可以简单地计算分子量的不确定度，计算中采用均匀分布。按照国家计量检定系统的说明，用于常量分析的工作基准试剂属于二级标准物质，在95%的置信概率下其不确定度为0.05%，因此得到其纯度的标准不确定度为0.05%/1.96=0.026%=2.6×10-4。但市售的某些工作基准试剂并不符合或不适用国家计量检定系统的要求，如给出的纯度为99.9±0.1%，这时可按均匀分布计算其标准不确定度，即0.1%/=5.8×10-4。在化学分析中，标准物质一般是用来核查测量系统的，而不是用于量值的计算的。因此，不应使用标准物质的标准值来修正被测量。但在不确定度的评定中，标准物质起到了关键作用。例如，进行加标回收试验时，为确定某一校正因子及其不确定度，经常使用标准物质。这里应该指出，加标回收试验的回收率必须在接近100%的一个狭窄的范围内，否则不应使用回收率校正被测量，而应重新设计或改进实验方法使其达到这一要求。因此标准物质标准值的不确定度实际上已在校正因子中计算，所以这里不能重复计算。23 总结化学分析中被测量与各分量的关系可以得出较完整的因果图，在这张因果图中，采用了随机效应与系统效应分离的方法。各分量的详细说明见前面的论述和图。在改进后的因果图中，实际上我们没有考虑到单次测试与多次测试的问题，因此在合成标准不确定度及以后的有关扩展不确定度的计算中会产生自由度的问题。由于重复性或再现性限值是由协同试验结果得出的，重复性标准差是不考虑再现性条件引起的组间标准偏差而得到的，再现性标准差则恰好相反，而一般方法中给出的重复性或再现性限值是重复性和再现性标准差乘以系数2而得到的。223 相当于扩展不确定度中的包含因子。作为引用该数据来说，是对被测量的这一分量的不确定度的一种B类评定方法。而重复性和再现性限值和标准差都是对单次试验结果而言的，它表明单次试验结果的分散程度。但是，取样和制样过程与测试的整体是对应的，也就是说，无论我们进行几次平行试验，其可接受的结果的平均值的不确定度才可与取样和制样的不确定度以1：1的关系合成的。因此，在合成标准不确定度时，还应考虑到测量次数的因素以及数值修约等因素。所以我们可以得到进一步改进的因果图。23 2.合成标准不确定度方法的探讨2.1合成方法与技巧在合成标准不确定度的理论和现行的方法中，都给出了两种合成方法，一种是求偏导数确定分量的灵敏系数的方法，另一种是采用相对标准不确定度进行合成的方法。当输入量相关时，合成的方法变得非常复杂。我们注意到，相对不确定度的合成方法是最简单的，它避免了过多的计算过程。但它有两个前提条件，一是输入量必须是相互独立的，二是被测量的函数形式必须是幂积的形式。同时我们还注意到，求偏导数的方法也必须在输入量相互独立或不相关的条件下才能避免求协方差或相关系数的复杂计算过程。由于分量的分组对最终不确定度的评定并没有影响，在可能的情况下，将被测量的计算公式转化成独立分量的幂积形式将给不确定度的评定带来方便。例如，在反滴定中使用空白与样品消耗的标准溶液的体积差，其计算公式形式如下：，（3）其中X为被测量，V0和V分别为空白和样品消耗的标准溶液体积，C为标准溶液浓度，f为换算系数，m为样品质量，这时，我们可以令V0-V=V1，则计算公式变为：，（4）成为幂积形式，先求出V1的不确定度后，再用相对不确定度合成。23 在计算公式的转化中，应尽量使公式中不出现相关的量，如式（2）所表示的水分测量的计算公式中，m0，m1，m2是独立测定的质量值，它们是相互独立的，可以通过求灵敏系数的方法求得被测量水分的不确定度。但如果将式（2）中的分子改为干燥损失量m’，将分母改成样品量m，那么这两个量就会相关，无论是简单地求灵敏系数还是采用相对不确定度的方法计算，都得不到正确的不确定度。2.2相关性讨论在化学分析中，变量的相关是普遍存在的，区分相关与不相关的基本依据是多维随机变量的联合分布函数是否等于其边缘分布函数的乘积。但这种方法操作性不强，因为输入量的概率分布函数往往是很复杂的，甚至从现有的资料中无法找到其分布的依据。实际上，对输入量相关性的考察，大多以实际经验来判断。2.3自由度的讨论及扩展不确定度的确定自由度是决定不确定度的分布情况的关键因素，也是确定扩展不确定度的一个重要参数。但在一般的化学分析中，都是在使用样本来估计总体，因此被测量一般符合正态分布，而其有效自由度很大，其包含因子可直接取2或3。3.总结23 化学分析中测量不确定度的评定方法具有某些共同的特点，其不确定度的主要来源有：质量、体积、样品的非均匀性、测试过程及外部数据，本文给出了处理上述原因导致的不确定度的通用方法。另外，对合成标准不确定度的方法和技巧进行了初步探讨。23'