关注高考生物试题和解题方式的数学化

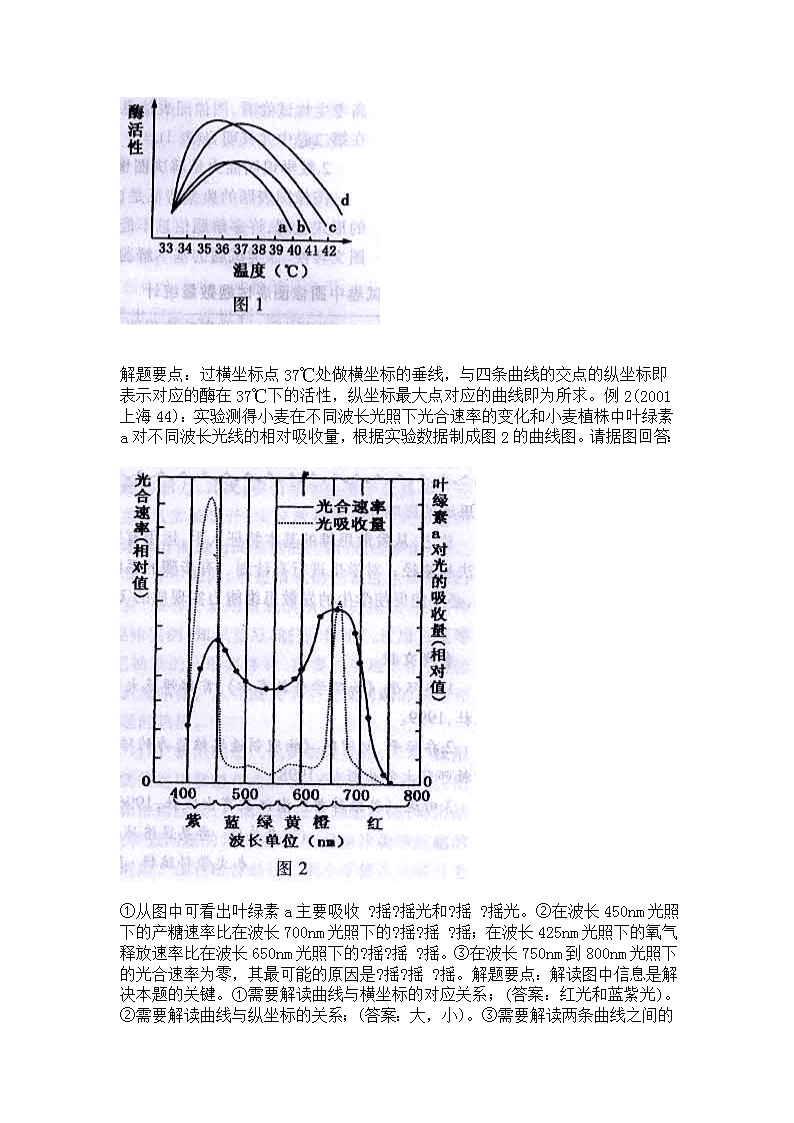
关注高考生物试题和解题方式的数学化贺建生物学作为科学的重要分支学科，科学的严密性与定量化是其重要特征。利用数学思想方法定量地研究生物学问题，是生物科学深入发展的标志之一。该特点反映在高考上，表现为问题解决与工具学科---数学学科的结合越来越紧密，解题方式的数学化越来越明显。具体体现在试题信息的图表化、问题考察的定量化和解题方法的数学化三个方面。一、高考生物试题题干信息的图表化1.试题信息的图表化是目前高考试题的显著特征试题信息的呈现形式总的说来可以分为文字信息、符号信息与图表信息三大类，试题信息的图表化是目前生物高考的显著特征之一。在高考《生物科考试说明》中明确要求："正确理解、分析生物学中以图表、图解等表达的内容和意义，并能用图表等多种表达形式准确地描述生物学现象和实验结果。"从近年高考生物试卷看，图像图表信息题占有突出的位置，在第二卷中尤其明显(表1)。2.数学识图能力是解决图像图表题的关键图像图表题的典型特征是试题信息以图像图表的形式呈现，许多解题信息不能直接获得，需要经过图文转换。该类试题的基本解题模式可以概括为："信息解读+生物学概念=问题解决"因此，图像图表信息的解读是问题解决的关键环节。根据图像属性，高考卷中的图像类型可以分为生物结构图、实验流程图、遗传图解、表格与曲线等五类。图像图表信息的解读从根本上说依赖于数学中的识图能力，其中曲线与表格两类试题信息的解读对数学能力的依赖尤其明显。(1)对曲线信息的解读曲线本质上是数学中的函数图像，对函数图像信息的解读包括理解自变量与因变量的关系、曲线每个点代表的含义、曲线的走向、极值、拐点以及不同曲线之间的关系等。例1(2000广东10)：图1为4种不同的酶(分别以a、b、c、d表示)在不同温度下酶活性变化的曲线。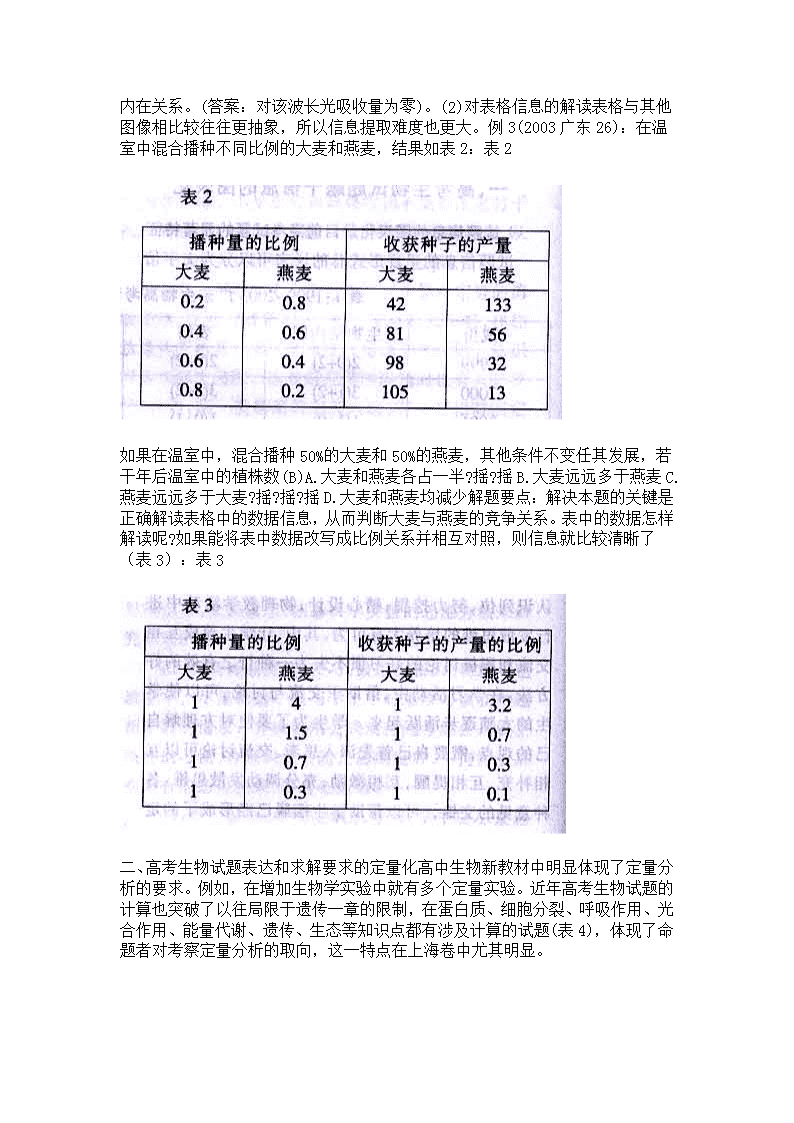在37℃时酶活性最高是A.a?摇B.bC.cD.d 解题要点：过横坐标点37℃处做横坐标的垂线，与四条曲线的交点的纵坐标即表示对应的酶在37℃下的活性，纵坐标最大点对应的曲线即为所求。例2(2001上海44)：实验测得小麦在不同波长光照下光合速率的变化和小麦植株中叶绿素a对不同波长光线的相对吸收量，根据实验数据制成图2的曲线图。请据图回答：①从图中可看出叶绿素a主要吸收?摇?摇光和?摇?摇光。②在波长450nm光照下的产糖速率比在波长700nm光照下的?摇?摇?摇；在波长425nm光照下的氧气释放速率比在波长650nm光照下的?摇?摇?摇。③在波长750nm到800nm光照下的光合速率为零，其最可能的原因是?摇?摇 ?摇。解题要点：解读图中信息是解决本题的关键。①需要解读曲线与横坐标的对应关系；(答案：红光和蓝紫光)。②需要解读曲线与纵坐标的关系；(答案：大，小)。③需要解读两条曲线之间的内在关系。(答案：对该波长光吸收量为零)。(2)对表格信息的解读表格与其他图像相比较往往更抽象，所以信息提取难度也更大。例3(2003广东26)：在温室中混合播种不同比例的大麦和燕麦，结果如表2：表2如果在温室中，混合播种50%的大麦和50%的燕麦，其他条件不变任其发展，若干年后温室中的植株数(B)A.大麦和燕麦各占一半?摇?摇B.大麦远远多于燕麦C.燕麦远远多于大麦?摇?摇?摇D.大麦和燕麦均减少解题要点：解决本题的关键是正确解读表格中的数据信息，从而判断大麦与燕麦的竞争关系。表中的数据怎样解读呢?如果能将表中数据改写成比例关系并相互对照，则信息就比较清晰了（表3）：表3二、高考生物试题表达和求解要求的定量化高中生物新教材中明显体现了定量分析的要求。例如，在增加生物学实验中就有多个定量实验。近年高考生物试题的计算也突破了以往局限于遗传一章的限制，在蛋白质、细胞分裂、呼吸作用、光合作用、能量代谢、遗传、生态等知识点都有涉及计算的试题(表4)，体现了命题者对考察定量分析的取向，这一特点在上海卷中尤其明显。 具体来说，近年高考生物试卷中的定量试题根据考察内容可以分成六类：1.定量考察氨基酸的缩合。计算缩合过程中生成的肽键数、水分子数，以及得到蛋白质分子的分子量。例4(2003上海29)：某蛋白质由n条肽链组成，氨基酸的平均分子量为a，控制蛋白质合成的基因含b个碱基对，则该蛋白质的分子量为(D)A.2ab/3-6b+10nB.ab/3-6bC.18(b/3-a)D.ab/3-18(b/3-n)2.定量考察有丝分裂和减数分裂中染色体和DNA的变化规律。例5(2000上海16)：在细胞有丝分裂的分裂期开始时，染色体数量为N，DNA含量为Q，则该细胞分裂后每个子细胞的染色体数量和DNA含量分别为(C)A.N和QB.N/2和Q/2C.N和Q/2D.N/2和Q3.定量考察新陈代谢中物质和能量的变化。主要是根据光合作用和呼吸作用化学方程式进行计算。例6(1998上海8)：酵母菌产生无氧呼吸产生A摩尔的CO。人在正常情况下消耗同样多的葡萄糖，可形成CO(D)A.7A/3molB.A/12molC.6AmolD.3Amol4.遗传计算。包括DNA分子中的碱基数量计算、DNA分子的复制计算、基因表达中碱基与氨基酸数量关系的计算以及遗传几率计算四类。例7(2003上海32)：某DNA分子共有a个碱基，其中含胞嘧啶m个，则DNA分子复制3次，需要游离的胸腺嘧啶脱氧核苷酸数为(C)A.7(a-m)B.8(a-m)C.7(a/2-m)?摇D.8(2a-m)5.定量考察基因频率和种群密度的变化。例8(2001上海36)：调查某草原田鼠数量时，在设置1公顷的调查区内，放置100个捕鼠笼，一夜间捕获鼠32头，将捕获的鼠经标记后在原地释放。数日后，在同一地方再放置同样数量的捕鼠笼，这次共捕获30头，其中有上次标记过的个体10头。请回答下列问题：(1)若该地区田鼠种群个体总数为N，则N=?摇 ?摇?摇头。(答案：96)(其余小题略)6.定量考察生态系统中能量传递的变化规律。例9：(1997上海26)在一个生态系统中，已知初级消费者与次级消费者的个体数分别为N、N，个体平均重量分别为M、M，则正确的是(A)A.N·M＞N·MB.N·M=N·MC.N·M＜N·MD.N·M＞N·M三、高考生物试题解题方法的数学化许多生物问题中渗透着重要的数学原理，在问题解决过程中体现着非常明显的数学思想。1.函数知识的运用函数思想是数学学科的核心思想，许多数学问题都是函数问题，许多生物学问题也都渗透着函数思想。(1)函数的极值问题例10(1999广东28)：在下列食物链中，假设初级消费者从生产者获得的能量数值相同，哪一条食物链提供给猫头鹰的能量最多?(D)A.绿色植物→蚌蝠→蜘蛛→撕蜴→蛇→猫头鹰B.绿色植物→蚌蝠→青蛙→蛇→猫头鹰C.绿色植物→鼠→蛇→猫头鹰D.绿色植物→鼠→猫头鹰解题要点：本题实质上是求函数的极值。猫头鹰与绿色植物的能量关系实质上是个函数关系，用常数a代表绿色植物(生产者)的总能量，常数b代表传递效率10%～20%，营养级的数量为自变量x，猫头鹰获得能量的函数表达式可以表示为：y=a·b(10%＜b＜20%,x为大于1的正整数)。(2)函数的单调性问题根据函数的单调性可以判断某个生物学变量的变化趋势。例11(2001广东19)：图3表示蛙的受精卵发育至囊胚过程中，DNA总量、每个细胞体积、所有细胞体积之和、有机物总量的变化趋势。其中正确的是(A)A.①②B.①③C.②④D.③④解题要点：本题用曲线的形式表示了发育过程中有机物、DNA、细胞体积与时间之间的函数关系。(3)不等式问题不等式也属于函数关系的一种类型。例12(2001广东11)：我国北方处于平衡状态的某森林生态系统，其碳素循环如图4，箭头和字母分别表示碳素传递方向和转移量。下列选项正确的是(A)A.夏季，a>b+c+eB.秋季，e+fc+f 2.排列组合与概率排列组合与概率是高中数学的重点与难点之一，也是解决多个生物学难点的工具，与排列组合和概率思想相结合的试题数量极多，如：(1)利用排列组合思想理解蛋白质的多样性；(2)利用排列组合思想理解核酸的多样性；(3)利用排列组合思想理解密码子与碱基组成的关系；(4)利用排列组合思想理解减数分裂过程中基因的自由组合；(5)利用概率论中的乘法原理和加法原理解决遗传几率计算。例13(2000广东21)：基因型为AaBb(这两对基因不连锁)的水稻自交，自交后代中两对基因都是纯合的个体占总数的(B)A.2/16B.4/16C.6/16D.8/16解题要点：第一对基因是纯合(AA或aa)的几率为1/2，第二对基因是纯合(BB或bb)的几率仍是1/2，根据乘法原理，两对都是纯合的向率为1/4。3.数学建模思想数学模型思想是利用数学方法原理建立模型解决实际问题的思想方法。中学生物在生物与环境部分与数学模型结合比较紧密，如：(1)利用数学模型解决种群数量的增长(J型增长与S型增长)；(2)利用数学模型解决生态系统中的能量流动；(3)建立数学模型解决遗传中F1连续自交后代中纯合体的比例变化；(4)建立数学模型估算种群数量(标志重捕法)。例14(2001上海36)：……若某种群有成鼠a头(计算时作为亲代)，每头雌鼠一生产仔16头，各代雌雄比例均为1∶1，子代幼鼠均发育为成鼠，所有个体的繁殖力均相等，则从理论上计算，第n代产生的子代数为?摇?摇?摇头。A.a×8?摇?摇B.a×8n+1C.a×8?摇?摇D.a×8解题要点：本题的解决过程，其实也就是数学建模过程---根据试题背景建立一个计算出生率的数学模型。(答案：C)4.集合思想集合思想多运用于遗传问题解决的分类处理，例如某个体有两种基因型，可以分成两种情况分别处理然后再叠加；再如，两种或多种遗传病同时遗传时，遗传概率的计算。其次，集合思想还可以用于表示具有包含关系的不同概念之间的关系，例如生存斗争、种内斗争、种间斗争；应激性、反射、条件反射、非条件反射等。例15(1997上海51)：为了说明近亲结婚的危害性，某医生向学员分析讲解了下列有白化病和色盲两种遗传病的家族系谱图。设白化病的致病基因为a，色盲的致病基因为b，请回答：…… (2)若Ⅲ-8与Ⅲ-10结婚，生育子女中只患白化病或色盲一种遗传病的概率是?摇?摇?摇?摇；同时患两种遗传病的概率是?摇?摇?摇?摇。……解题要点：可以先算出白化病的发病率为1/3，色盲的发病率为1/4，然后利用集合思想计算：①只患一种病的概率为图中空白部分的并集：?摇［P白化-(P白化×P色盲)］+?摇［P色盲-(P白化×P色盲)］=［1/3+1/4］-2［1/3×1/4］=5/12②同时患两种遗传病的概率是二者的交集：P×P=5/12利用类似方法还可以计算总的患病概率(二者的并集)：?摇P+P-(P×P)=1/3+1/4-［1/3×1/4］=1/2解题思维的数学化是高考试题发展的重要趋势之一，在备考过程中教师应该采取积极措施提升学生数学素养，提高学生解题技巧和解题水平。具体建议如下：(1)教师要有意识地引导学生将数学学科中训练形成的识图能力和方法迁移到生物学科，把数学工具积极主动地运用到生物试题的解决过程中。(2)生物教师的平时的教学中与数学教师协作，将生物学问题引入数学课堂，强化学科渗透，强化数、生联系。(3)对于比较复杂的遗传计算可以采用"案例教学"的办法，首先让学生掌握一个典型范例的解题方法和原理，使学生在解题过程中遇到疑惑时可以与范例相比较进而解决问题。(作者单位摇华南师大附中本文学科编辑钟