结构力学课件：结构动力学-3

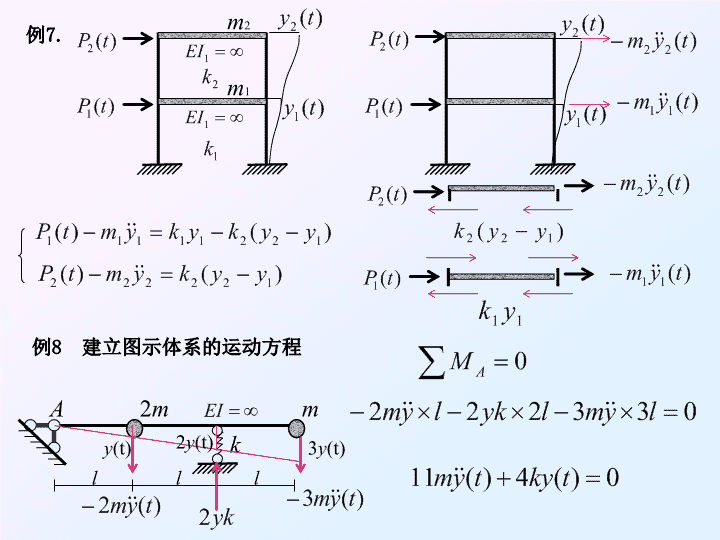
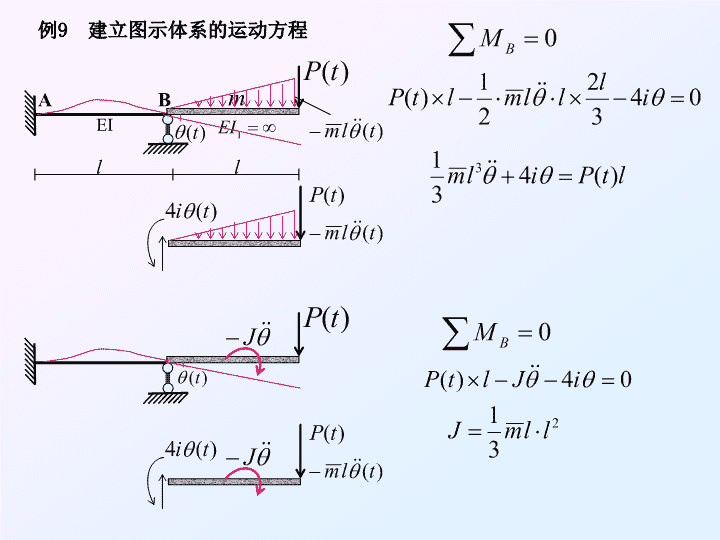
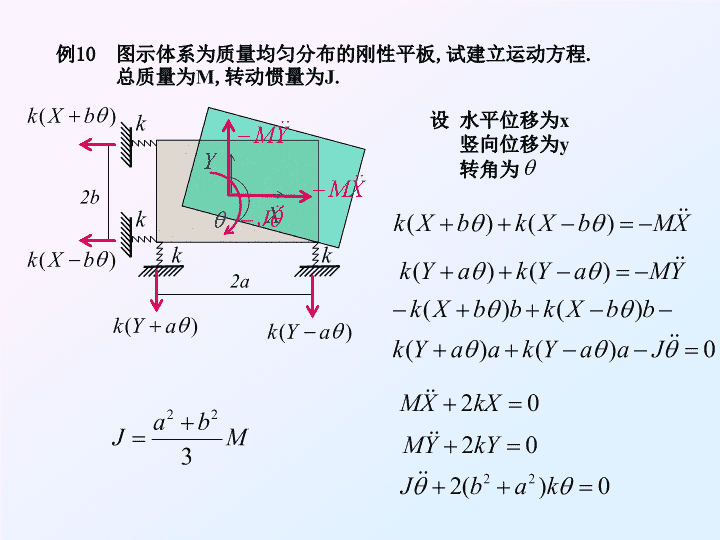
例7.m1m2例8建立图示体系的运动方程m2mlllkAy(t)2y(t)3y(t) llEIm例9建立图示体系的运动方程AB 例10图示体系为质量均匀分布的刚性平板,试建立运动方程.总质量为M,转动惯量为J.设水平位移为x竖向位移为y转角为2b2a 2.单自由度体系的振动分析2.1不计阻尼自由振动自由振动---由初位移、初速度引起的,在振动中无动荷载作用的振动。分析自由振动的目的---确定体系的动力特性：频率、周期。一.运动方程及其解阻尼---耗散能量的作用。mEIl令二阶线性齐次常微分方程 一.运动方程及其解mEIl令二阶线性齐次常微分方程其通解为由初始条件可得令其中 二.振动分析其通解为由初始条件可得令其中单自由度体系不计阻尼时的自由振动是简谐振动.自振周期自振园频率(自振频率)与外界无关,体系本身固有的特性A振幅初相位角 二.振动分析单自由度体系不计阻尼时的自由振动是简谐振动.自振周期自振园频率(自振频率)与外界无关,体系本身固有的特性A振幅初相位角三.自振频率和周期的计算1.计算方法(1)利用计算公式(2)利用机械能守恒 三.自振频率和周期的计算1.计算方法(1)利用计算公式(2)利用机械能守恒(3)利用振动规律位移与惯性力同频同步.1mEIl幅值方程 三.自振频率和周期的计算2.算例例一.求图示体系的自振频率和周期.mEIlEIl=1=1ll/2l解: 例二.求图示体系的自振频率和周期.=1解:mEIllm/2EIEIll例三.质点重W,求体系的频率和周期.解:EIkl1k 例四.求图示体系的自振频率和周期.解:mlmmlllkk1.能量法2.列幅值方程A 2.2简谐荷载作用下的受迫振动(不计阻尼)一.运动方程及其解二阶线性非齐次常微分方程受迫振动---动荷载引起的振动.mEIlP(t)P---荷载幅值---荷载频率运动方程或通解其中设代入方程,可得通解为 二.纯受迫振动分析mEIlP(t)设代入方程,可得通解为---荷载幅值作为静荷载所引起的静位移---动力系数---稳态振幅 11---频比二.纯受迫振动分析mEIlP(t)---荷载幅值作为静荷载所引起的静位移---动力系数---稳态振幅 11---荷载幅值作为静荷载所引起的静位移---动力系数---频比---稳态振幅---共振增函数减函数为避开共振一般应大于1.25或小于0.75.1.250.75共振区 若要使振幅降低,应采取何种措施?通过改变频比可增加或减小振幅.增函数减函数---共振为避开共振一般应大于1.25或小于0.75.应使频比减小.增加结构自频.增加刚度、减小质量.应使频比增大.减小结构自频.减小刚度、增大质量. 作业:145页6-7(d)(e)6-9165页7-1(a)(c)(d)(e)