结构力学课件：有限单元法-1

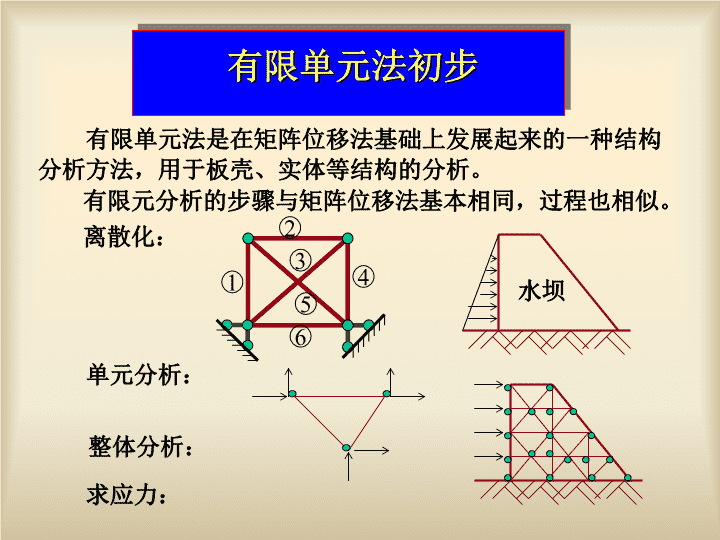
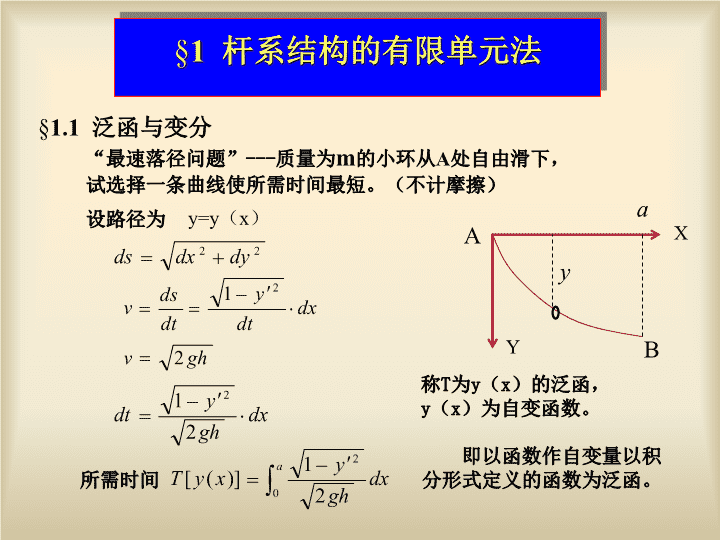
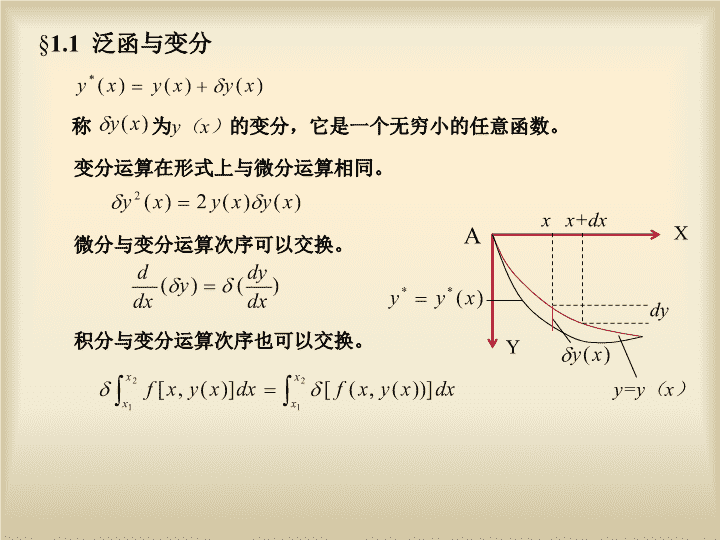
有限单元法初步有限单元法是在矩阵位移法基础上发展起来的一种结构分析方法，用于板壳、实体等结构的分析。有限元分析的步骤与矩阵位移法基本相同，过程也相似。124635离散化：水坝单元分析：整体分析：求应力： 1杆系结构的有限单元法1.1泛函与变分“最速落径问题”---质量为m的小环从A处自由滑下，试选择一条曲线使所需时间最短。（不计摩擦）ABXY设路径为y=y（x）所需时间ay称T为y（x）的泛函，y（x）为自变函数。即以函数作自变量以积分形式定义的函数为泛函。 1.1泛函与变分XAY变分运算在形式上与微分运算相同。y=y（x）x+dxdyx称为y（x）的变分，它是一个无穷小的任意函数。微分与变分运算次序可以交换。积分与变分运算次序也可以交换。 1.2变形体虚位移原理外力虚功内力虚功虚功方程1.3势能原理1.应变能弯曲应变能P拉压应变能PP剪切应变能y（x）平衡位置q(x) 2.外力势能1.3势能原理1.应变能弯曲应变能PP拉压应变能P剪切应变能外力从变形状态退回到无位移的原始状态中所作的功.y(x)q(x)3.结构势能1.2变形体虚位移原理虚功方程y（x）平衡位置q(x) 1.2变形体虚位移原理虚功方程y（x）平衡位置q(x)2.外力势能1.3势能原理1.应变能弯曲应变能拉压应变能剪切应变能外力从变形状态退回到移的原始状态中所作的功.3.结构势能对于线弹性杆件体系 1.2变形体虚位移原理虚功方程y（x）平衡位置q(x)1.3势能原理4.势能原理对于线弹性杆件体系对于线弹性杆件体系,虚功方程为:或即在弹性结构的一切可能位移中，真实位移使结构势能取驻值。满足结构位移边界条件的位移 1.4基于势能原理的平面拉压杆单元的单元分析单元杆端力一、建立位移模式---用杆端位移表示杆中位移EA,leq(x)21单元杆端位移设杆中任一点位移a、b称为广义坐标令---自然坐标形(状)函数时的杆中位移.时的杆中位移.---形函数矩阵形函数性质:1.若2.中包含刚体位移 1.4基于势能原理的平面拉压杆单元的单元分析EA,leq(x)21杆中任一点应变一、建立位移模式---用杆端位移表示杆中位移---应变矩阵二、应变分析---用杆端位移表示杆中应变三、应力分析---用杆端位移表示杆中内力杆中任一点应力杆中任一截面的轴力 1.4基于势能原理的平面拉压杆单元的单元分析EA,leq(x)21一、建立位移模式---用杆端位移表示杆中位移二、应变分析---用杆端位移表示杆中应变三、应力分析---用杆端位移表示杆中内力四、单元分析---用杆端位移表示杆端力单元应变能单元外力势能 1.4基于势能原理的平面拉压杆单元的单元分析EA,leq(x)21四、单元分析---用杆端位移表示杆端力单元应变能单元外力势能单元的总势能单元是平衡的 1.4基于势能原理的平面拉压杆单元的单元分析EA,leq(x)21单元的总势能单元是平衡的上式记作其中--局部坐标系下的单元刚度矩阵--单元等效结点荷载 1.4基于势能原理的平面拉压杆单元的单元分析单元分析的步骤:1.以单元结点位移表示单元内位移,的性函数矩阵2.由应变分析得到应变矩阵3.由势能驻值原理或变形体虚功原理建立单元刚度方程得到单刚与单元等效结点荷载坐标转换与矩阵位移法相同