结构力学课件：虚功原理

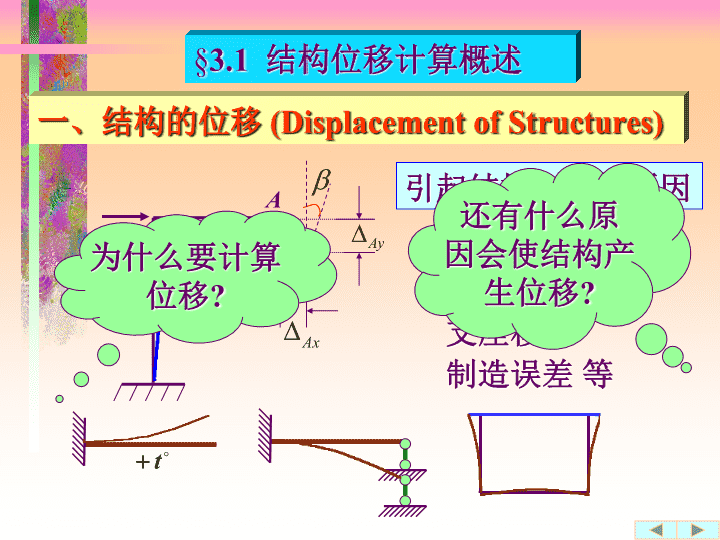
第三章静定结构的位移计算DisplacementofStaticallyDeterminateStructures 3.1结构位移计算概述一、结构的位移(DisplacementofStructures)A位移转角位移线位移A点线位移A点水平位移A点竖向位移A截面转角P 3.1结构位移计算概述一、结构的位移(DisplacementofStructures)AP引起结构位移的原因制造误差等荷载温度改变支座移动还有什么原因会使结构产生位移?为什么要计算位移? 铁路工程技术规范规定:二、计算位移的目的(1)刚度要求在工程上，吊车梁允许的挠度<1/600跨度；桥梁在竖向活载下，钢板桥梁和钢桁梁最大挠度<1/700和1/900跨度高层建筑的最大位移<1/1000高度。最大层间位移<1/800层高。(2)超静定、动力和稳定计算(3）施工要求 （3）理想联结(IdealConstraint)。三、本章位移计算的假定叠加原理适用（principleofsuperposition)(1)线弹性(LinearElastic),(2)小变形(SmallDeformation),四、计算方法单位荷载法(Dummy-UnitLoadMethod) 3.2变形体虚功原理(PrincipleofVirtualWork)一、功(Work)、实功(RealWork)和虚功(VirtualWork)功：力对物体作用的累计效果的度量功=力×力作用点沿力方向上的位移实功：力在自身所产生的位移上所作的功虚功：力在非自身所产生的位移上所作的功 3.2变形体虚功原理(PrincipleofVirtualWork)一、功(Work)、实功(RealWork)和虚功(VirtualWork)力状态位移状态（虚力状态）（虚位移状态）注意：（1）属同一体系；（2）均为可能状态。即位移应满足变形协调条件；力状态应满足平衡条件。（3）位移状态与力状态完全无关； 3.2变形体虚功原理(PrincipleofVirtualWork)二、广义力(Generalizedforce)、广义位移(Generalizeddisplacement)一个力系作的总虚功W=P×P---广义力;---广义位移例:1)作虚功的力系为一个集中力2)作虚功的力系为一个集中力偶3)作虚功的力系为两个等值反向的集中力偶4)作虚功的力系为两个等值反向的集中力 （1）质点系的虚位移原理具有理想约束的质点系，在某一位置处于平衡的必要和充分条件是：三、变形体的虚功原理Σfiδri=0→→.对于任何可能的虚位移，作用于质点系的主动力所做虚功之和为零。也即 （2）刚体系的虚位移原理去掉约束而代以相应的反力，该反力便可看成外力。则有：刚体系处于平衡的必要和充分条件是：对于任何可能的虚位移，作用于刚体系的所有外力所做虚功之和为零。PΔ2Δ3Δ/2 原理的表述：任何一个处于平衡状态的变形体，当发生任意一个虚位移时，变形体所受外力在虚位移上所作的总虚功δWe，恒等于变形体各微段外力在微段变形位移上作的虚功之和δWi。也即恒有如下虚功方程成立δWe=δWi（3）变形体的虚功原理 任何一个处于平衡状态的变形体，当发生任意一个虚位移时，变形体所受外力在虚位移上所作的总虚功δWe,恒等于变形体各微段外力在微段变形位移上作的虚功之和δWi。变形体虚功原理的证明:1.利用变形连续性条件计算所有微段的外力虚功之和W微段外力分为两部分体系外力相互作用力微段外力功分为两部分体系外力功dWe相互作用力功dWn微段外力功dW=dWe+dWn所有微段的外力功之和:W=∫dWe+∫dWn=∫dWe=δWe2.利用平衡条件条件计算所有微段的外力虚功之和W微段外力功分为两部分在刚体位移上的功dWg在变形位移上的功dWi微段外力功dW=dWg+dWi所有微段的外力功之和:W=∫dWi=δWi微段位移分为两部分刚体位移变形位移故有δWe=δWi成立。 任何一个处于平衡状态的变形体，当发生任意一个虚位移时，变形体所受外力在虚位移上所作的总虚功δWe,恒等于变形体各微段外力在微段变形位移上作的虚功之和δWi。变形体虚功原理的证明:1.利用变形连续性条件计算所有微段的外力虚功之和W微段外力分为两部分体系外力相互作用力微段外力功分为两部分体系外力功dWe相互作用力功dWn微段外力功dW=dWe+dWn所有微段的外力功之和:W=∫dWe+∫dWn=∫dWe=δWe2.利用平衡条件条件计算所有微段的外力虚功之和W微段外力功分为两部分在刚体位移上的功dWg在变形位移上的功dWi微段外力功dW=dWg+dWi所有微段的外力功之和:W=∫dWi=δWi微段位移分为两部分刚体位移变形位移故有δWe=δWi成立。几个问题:1.虚功原理里存在两个状态：力状态必须满足平衡条件；位移状态必须满足协调条件。因此原理仅是必要性命题。2.原理的证明表明:原理适用于任何(线性和非线性)的变形体，适用于任何结构。3.原理可有两种应用：实际待分析的平衡力状态，虚设的协调位移状态，将平衡问题化为几何问题来求解。实际待分析的协调位移状态，虚设的平衡力状态，将位移分析化为平衡问题来求解。 δWi的计算:δWi=Σ∫[Nδε+Qδγ+Mδθ]ds微段外力:微段变形可看成由如下几部分组成:（4）变形体虚功方程的展开式微段剪切微段拉伸微段弯曲对于直杆体系，由于变形互不耦连，有:δWe=Σ∫[Nδε+Qδγ+Mδθ]ds 四、虚功原理的两种应用1）虚功原理用于虚设的协调位移状态与实际的平衡力状态之间。例.求A端的支座反力(ReactionatSupport)。解：去掉A端约束并代以反力X，构造相应的虚位移状态.ABaC(a)bPX(b)P(c)直线待分析平衡的力状态虚设协调的位移状态由外力虚功总和为零，即：将代入得:通常取单位位移法(Unit-DisplacementMethod)(1)对静定结构，这里实际用的是刚体虚位移原理，实质上是实际受力状态的平衡方程(2)虚位移与实际力状态无关,故可设(3)求解时关键一步是找出虚位移状态的位移关系。(4)用几何法来解静力平衡问题 例.求A端支座发生竖向位移c时引起C点的竖向位移.2）虚功原理用于虚设的平衡力状态与实际的协调位移状态之间。解：首先构造出相应的虚设力状态。即，在拟求位移之点（C点）沿拟求位移方向（竖向）设置单位荷载。ABaCbc1ABC由求得：解得：这是单位荷载法(Dummy-UnitLoadMethod)它是Maxwell,1864和Mohr,1874提出，故也称为Maxwell-MohrMethod(1)所建立的虚功方程,实质上是几何方程。(2)虚设的力状态与实际位移状态无关，故可设单位广义力P=1(3)求解时关键一步是找出虚力状态的静力平衡关系。(4)是用静力平衡法来解几何问题。虚功方程为： 单位位移法的虚功方程平衡方程单位荷载法的虚功方程几何方程第一种应用一些文献称为“虚位移原理”，而将第二种应用称为“虚力原理”。更确切的说法为，两种应用的依据是上述两原理的必要性命题。上述两原理都是充分、必要性命题，它们和虚功原理是有区别的。虚位移原理:一个力系平衡的充分必要条件是:对任意协调位移,虚功方程成立.虚力原理:一个位移是协调的充分必要条件是:对任意平衡力系,虚功方程成立”。