结构力学课件：有限单元法-2

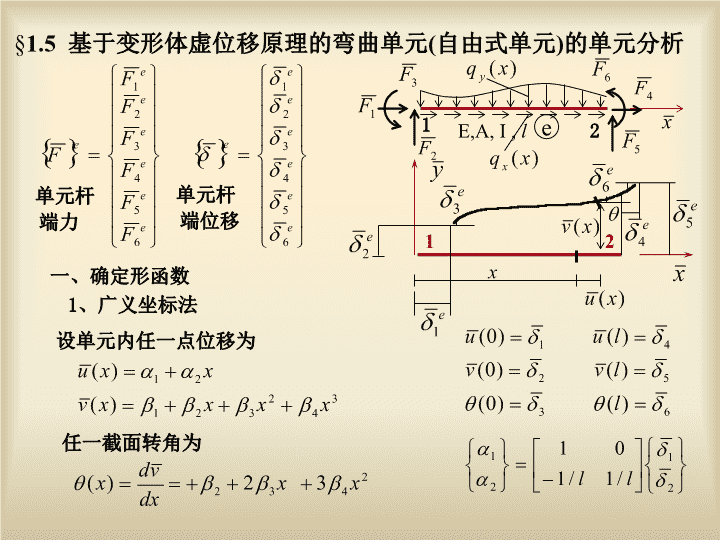
1.5基于变形体虚位移原理的弯曲单元(自由式单元)的单元分析设单元内任一点位移为E,A,I,le2112单元杆端力单元杆端位移一、确定形函数x1、广义坐标法任一截面转角为 1.5基于变形体虚位移原理的弯曲单元(自由式单元)的单元分析E,A,I,le2112x设单元内任一点位移为一、确定形函数1、广义坐标法任一截面转角为 1.5基于变形体虚位移原理的弯曲单元(自由式单元)的单元分析E,A,I,le2112x 1.5基于变形体虚位移原理的弯曲单元(自由式单元)的单元分析E,A,I,le2112x 1.5基于变形体虚位移原理的弯曲单元(自由式单元)的单元分析E,A,I,le2112x为发生杆端位移时,杆中位移。如：为发生杆端位移时,杆中竖向位移。xx 1.5基于变形体虚位移原理的弯曲单元(自由式单元)的单元分析E,A,I,le2112x为发生杆端位移时,杆中位移。如：为发生杆端位移时,杆中竖向位移。xx 1.5基于变形体虚位移原理的弯曲单元(自由式单元)的单元分析一、确定形函数2、试凑法利用形函数的性质建立形函数矩阵(1)确定由可设由可知所以(2)确定由可设 1.5基于变形体虚位移原理的弯曲单元(自由式单元)的单元分析一、确定形函数二、确定应变矩阵(建立几何方程)微分算子矩阵 1.5基于变形体虚位移原理的弯曲单元(自由式单元)的单元分析一、确定形函数二、确定应变矩阵(建立几何方程)弹性矩阵三、确定弹性矩阵(建立物理方程)物理方程四、确定单刚和单元等效结点荷载(建立平衡方程)E,A,I,le2112x 1.5基于变形体虚位移原理的弯曲单元(自由式单元)的单元分析E,A,I,le2112x 1.5基于变形体虚位移原理的弯曲单元(自由式单元)的单元分析单刚单元等效结点荷载(i,j=1,2) 1.5基于变形体虚位移原理的弯曲单元(自由式单元)的单元分析 形函数矩阵是那两组量之间的联系矩阵?应变矩阵是那两个量之间的联系矩阵?弹性矩阵是那两个量之间的联系矩阵?单刚是那两个量之间的联系矩阵?单元分析的步骤是怎样的?作业:1.推导自由式单元形函数2.推导连续梁单元的单刚.位移模式取