材料力学课件第七章弯曲变形.ppt

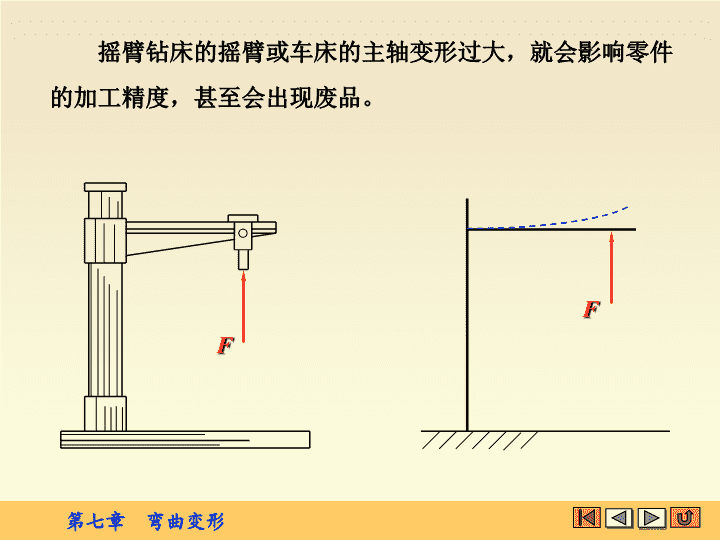
第7章弯曲变形※工程问题中的弯曲变形※挠曲线的近似微分方程※用积分法求弯曲变形※用叠加法求弯曲变形※简单静不定梁※提高弯曲刚度的措施 §7-1概述在工程实践中，对某些受弯构件，除要求具有足够的强度外，还要求变形不能过大，即要求构件有足够的刚度，以保证结构或机器正常工作。一、工程实践中的弯曲变形问题 摇臂钻床的摇臂或车床的主轴变形过大，就会影响零件的加工精度，甚至会出现废品。FF 桥式起重机的横梁变形过大,则会使小车行走困难，出现爬坡现象。PP 但在另外一些情况下，有时却要求构件具有较大的弹性变形，以满足特定的工作需要。例如，车辆上的板弹簧，要求有足够大的变形，以缓解车辆受到的冲击和振动作用。 二、弯曲变形的基本概念FxlxABl描述截面上任一点的位移:1、形心轴的线位移——挠度v2、截面绕形心轴的角位移——转角 ABF二、弯曲变形的基本概念xlxlF变弯的形心轴——挠曲线F挠度随坐标变化的方程——挠曲线方程F忽略剪切变形+梁的转角一般很小—— §7-2梁挠曲线的近似微分方程中性层曲率表示的弯曲变形公式由高等数学知识挠曲轴微分方程（推广到非纯弯）（纯弯） 正负号确定——确定坐标系:v向上为正,逆时针为正.方程简化小变形时：xvxv §7-3用积分法求弯曲变形FC、D为积分常数，它由位移边界与连续条件确定。 边界条件：梁截面的已知位移条件连续条件：分段处挠曲轴应满足的连续、光滑条件连续:光滑:ACDMFB$挠曲线在B、C点连续且光滑 可动铰:自由端：无位移边界条件固定端:连续条件：边界条件：ABCDFE例1：写出梁的挠曲轴方程的边界条件和连续条件 例2：已知梁的抗弯刚度为EI。试求图示简支梁在均布载荷q作用下的转角方程、挠曲线方程，并确定max和vmax。l lxxy解：由边界条件：得： lxxy梁的转角方程和挠曲线方程分别为：最大转角和最大挠度分别为： 例3：已知梁的抗弯刚度为EI。试求图示悬臂梁在集中力P作用下的转角方程、挠曲线方程，并确定max和vmax。xyABPlx解：由边界条件：得： xyABPlx梁的转角方程和挠曲线方程分别为：最大转角和最大挠度分别为： xy例4：已知梁的抗弯刚度为EI。试求图示简支梁在集中力P作用下的转角方程、挠曲线方程，并确定max和vmax。ABPCx xy解：AC段:ABPCx由对称条件：由边界条件：得：得： xyABPCxAC段梁的转角方程和挠曲线方程分别为：最大转角和最大挠度分别为： 画挠曲线的大致形状ADBC+_Q+MF根据弯矩图定凹凸性，F弯矩图过零点处为拐点，F支座限定支座处的位移。凹凸凹直线大致形状 §7-4用叠加法求弯曲变形一、用叠加法计算梁的变形当梁上同时作用几个载荷时，各个载荷所引起的变形是各自独立的，互不影响。若计算几个载荷共同作用下在某截面上引起的变形，则可分别计算各个载荷单独作用下的变形，然后叠加。在材料服从胡克定律、且变形很小的前提下,载荷与它所引起的变形成线性关系。 MP例5：用叠加法求vC、A、B。 PM PM 例6：若图示梁B端的转角B=0，则力偶矩M等于多少？PMABaCaMABCPABC解： 例7:求图示外伸梁C点的挠度和转角。仅考虑BC段变形(刚化AB,可视BC为悬臂梁)ABC静定梁或刚架的任一横截面的总位移，等于各梁段单独变形(其余梁段刚化)在该截面引起的位移的代数和或矢量和ABC ABCABC仅考虑AB段变形(刚化BC)ABCqaqa2/2 例8：已知E为常数，I2=2I1，求WC，C。FABC FABC刚化AB段：ABCF仅考虑BC段变形：刚化BC段：F仅考虑AB段变形： FABCABCFF FABCEFABCEFABCEFABC对称性在变形分析中的应用F/2CFB例9：已知E为常数，I2=2I1，求WC，B。 例10：利用对称性求下面梁中点挠度与转角反对称,挠度为0(弯矩为0,拐点)对称,转角为0qACBBACq/2ACq/2 反对称,挠度为0(弯矩为0,拐点)ACq/2Cq/2 二、梁的刚度计算刚度条件：[v]、[]是构件的许可挠度和转角，它们决定于构件正常工作时的要求。 CL9TU40例11：图示工字钢梁，l=8m，Iz=2370cm4,Wz=237cm3，[v]=l／500，E=200GPa，[]=100MPa。试根据梁的刚度条件，确定梁的许可载荷[P]，并校核强度。PzI20a 解：由刚度条件:因此满足强度要求 §7-5用变形比较法解静不定梁静不定度与多余约束多余约束凡是多余维持平衡所必须的约束多余反力与多余约束相应的支反力或支力偶矩静不定度＝支反力（力偶）数－有效平衡方程数静不定度＝多余约束数5-3=2度静不定6-3=3度静不定 相当系统：受力与原静不定梁相同的静定梁，相当系统的选择不是唯一的。相当系统1相当系统2相当系统qABAFBqABABMA 总结：分析方法与分析步骤1、判断静不定度（确定多余约束数）；2、解除多余约束，建立相当系统；3、列出多余约束处的变形协调条件(位移边界条件)；4、结合平衡方程，求多余支反力。解除多余约束，代之以支反力；分析相当系统，使多余约束点处满足位移边界条件F静定基相当系统不唯一，一般选择求解起来最简单的一种。方法：步骤： AB静定基:相当系统：AB静定基与相当系统的选取：qABFBqABABMA 例12：求图示梁的支反力。qABFBqAB解：解除多余约束，建立相当系统。2.建立变形协调条件3.联立求解 qAB解2：解除多余约束，建立相当系统。2.建立变形协调条件3.联立求解ABMA 例13：为了提高悬臂梁AB的强度和刚度，用短梁CD加固。设二梁EI相同，试求：(1)二梁接触处的压力；(2)加固前后AB梁最大弯矩的比值；(3)加固前后B点挠度的比值。aaABCDP ABCDPFD解：(1)变形协调条件 解：(2)加固前后AB梁的最大弯矩ABPPABFD 解：(3)加固前后B点挠度ABPPABFD ABAB存在装配误差的静不定问题分析 例:直径为d的圆截面梁,支座B下沉，max=?AB解： §7-6提高弯曲刚度的措施依据对比强度问题或让材料远离截面中性轴，例如例如工字形与盒形薄壁截面与梁的合理强度设计相似点与的比较合理安排约束与加载方式（分散载荷等） 合理安排约束与加载方式lqqFq=F/l （1）强度是局部量，刚度是整体量（积分）.辅梁、等强度梁是合理强度设计的有效手段，提高梁的刚度须整体加强小孔显著影响强度，但对刚度影响甚微与梁的合理强度设计的不同点 (2)强度与材料和相关,刚度与E相关高强度钢一般不提高E钢与合金钢:E=200~220GPa铝合金:E=70~72GPa(3)刚度对梁的跨度更敏感F 跨度微小改变，将导致挠度显著改变例如l缩短20％，dmax将减少48.8%梁跨度的合理选取F3maxlµd 谢谢使用