材料力学课件3.（第2章-扭转和弯曲内力）.pdf

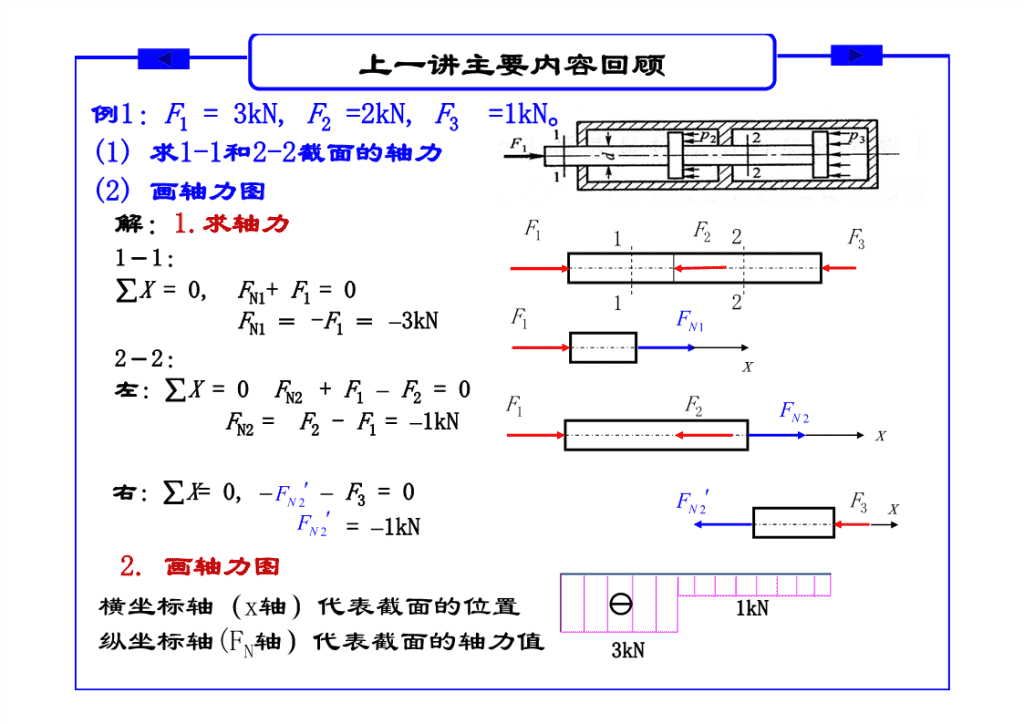
哈尔滨工业大学本科生课第2章内力及内力图§2.3扭转§2.4梁的平面弯曲及其计算简图§2.5梁的内力——剪力与弯矩 上一讲主要内容回顾mFF左端：∑X=0,FN–F=0mFN=FFNF﹜x轴力的符号规定：拉正压负ABFNABFFFNCBC2 上一讲主要内容回顾例1：F=3kN,F=2kN,F=1kN。123(1)求1-1和2-2截面的轴力(2)画轴力图解：1.求轴力F11F22F31－1：∑X=0,F+F=0N1112FFFN1＝-F1＝–3kN1N12－2：x左：∑X=0F+F–F=0N212F1F2FN2FN2=F2-F1=–1kNx右：∑X=0,––FN2F3=0FFN23xFN2=–1kNFN2.画轴力图基线x横坐标轴（x轴）代表截面的位置1kN纵坐标轴(FN轴）代表截面的轴力值3kN 上一讲主要内容回顾低碳钢的拉伸试验一条线二个规律三个现象四个阶段五个性能指标 哈尔滨工业大学本科生课§2.3扭转5 §2.3扭转1.扭转的工程实例螺丝刀杆工作时受扭Me主动力偶阻抗力偶 §2.3扭转1.扭转的工程实例汽车方向盘的转动轴工作时受扭 §2.3扭转1.扭转的工程实例机器中的传动轴工作时受扭 §2.3扭转2.扭转的概念受力特点：一对大小相等、转向相反、作用平面垂直于杆轴线的外力偶变形特点：杆件的任意两个横截面发生相对转动扭转角：杆件扭转时任意两个横截面发生相对转动而产生的相对角位移以扭转变形为主的杆件——轴 §2.3扭转3.求扭转内力的方法—截面法MeⅠⅠMe4.受扭圆轴横截面上的内力、内力偶矩—扭矩，ＴMeIMIeTTII §2.3扭转5.扭矩的符号规定—右手螺旋法则M扭矩的符号规定：IIeTTTIIMIIeTTTII右手法则：右手四指内屈，与扭矩转向相同，则拇指的指向表示扭矩矢的方向，若扭矩矢方向与截面外法线相同，规定扭矩为正，反之为负。 §2.3扭转例1计算1-1,2-2,3-3横截面上的扭矩5Ｍe1.5Ｍe1.5Ｍe2Ｍe13131.5Me1.5Me5Me2MeBCAD §2.3扭转1.5Me1.5Me5Me2Me123B1C2A3D1.5Me解：1-1截面，取左侧为脱离体1T1xT.15M0T.15M1e1e1B2-2截面，仍取左侧为脱离体1.5Me1.5MeT.15M.15M022eeT2TM32exB2A2Me3T3-3截面，取右侧为脱离体3xTM320eTM32e3D §2.3扭转1.5Me1.5Me5Me2Me123B1C2A3DT.15MTM3TM21e2e3e扭矩图2MTe15.Me3Me §2.3扭转1.5Me1.5Me2Me5Me123B1C2A3DT.15MTM3TM-51e2e3e扭矩图T15.Me3Me5Me2MTe15.Me3Me主动轴在中间的布置方式更合理 §2.3扭转工程中，通常不是直接给出作用在传动轴上的外力偶轴传递的功率P单位:kW轴的转速n单位:r/min,rpm §2.3扭转轴传递的功率P单位:kW轴的转速n单位:r/min,rpm每分钟做的功为WP31060PM9554力偶做功（每分钟）WMMn2eeen3WWPM1060e2n §2.3扭转例2传动轴的转速n=300r/min；主动轮输入的功率P=500kW，1三个从动轮输出的功率分别为：N=150kW，N=150kW，N=234200kW。试作轴的扭矩图。500M(9554)Nmk159.Nm1300150MM(9554)Nmk478.Nm23100200M(9554)Nmk637.Nm4300 §2.3扭转4.784.7815.96.37123B1C2A3DT.478KNmT.956KNmT.637KNm123扭矩图637.KNmT478.KNm956.KNm 哈尔滨工业大学本科生课§2.4梁的平面弯曲和计算简图20 §2.4梁的平面弯曲及其计算简图1.弯曲的工程实例工厂厂房的天车大梁 §2.4梁的平面弯曲及其计算简图1.弯曲的工程实例吊车梁 §2.4梁的平面弯曲及其计算简图1.弯曲的工程实例火车轮轴 §2.4梁的平面弯曲及其计算简图1.弯曲的工程实例阳台的挑梁楼房的横梁 §2.4梁的平面弯曲及其计算简图1.弯曲的工程实例上海长江大桥上海长江大桥第53号至54号桥墩间的“百米长梁”。这一箱梁长105米、宽16米、高5米，重2300吨，实现了桥梁史上的一大突破。 §2.4梁的平面弯曲及其计算简图2.弯曲的概念受力特点——作用于杆件上的外力都垂直于杆的轴线。变形特点——杆轴线由直线变为曲线。主要产生弯曲变形的杆---梁 §2.4梁的平面弯曲及其计算简图3.平面弯曲的概念讨论杆的弯曲暂时限制在如下的范围:杆的横截面至少有一根对称轴（一个对称面）对称轴对称轴对称轴对称轴 §2.4梁的平面弯曲及其计算简图工字型梁和T梁 §2.4梁的平面弯曲及其计算简图x梁的轴线y纵向对称轴纵向对称面纵向对称面：梁的轴线与横截面的对称轴（纵向对称轴）所构成的平面 §2.4梁的平面弯曲及其计算简图Fmq梁的轴线xMAy纵向对称轴集中力FFAB分布力载荷梁上的外力集中力偶支撑——支座反力（支反力） §2.4梁的平面弯曲及其计算简图平面弯曲受力特点：所有外力（载荷和支座反力）作用在纵向对称面内，并垂直于轴线变形特点：轴线由直线变成了在纵向对称面内的平面曲线。 §2.4梁的平面弯曲及其计算简图4.梁的计算简图x梁的轴线y纵向对称轴(1).用梁的轴线来代替实际的梁Fqxy §2.4梁的平面弯曲及其计算简图4.梁的计算简图(2)根据支座对梁在载荷平面内的约束情况支座简化的三种形式：固定绞支座可动绞支座固定端支座可转动，不能移动可转动和水平移动不能移动、不能转动 §2.4梁的平面弯曲及其计算简图工程中，常见的静定梁的计算简图有以下三种：简支梁一端是固定铰支约束另一端可动铰支约束悬臂梁一端为固定端另一端自由外伸梁绞支座支撑梁的一端或两端伸于支座之外 §2.4梁的平面弯曲及其计算简图楼房的横梁：阳台的挑梁： 哈尔滨工业大学本科生课§2.5梁的内力——剪力与弯矩36 §2.5梁的内力——剪力与弯矩FnanlFMMFaFsF——剪力M——弯矩sFMsFFFlaFlFlMFlaFl()0MFa §2.5梁的内力——剪力与弯矩剪力和弯矩的正负号规则：左上右下为正FsFsFsFs上压下拉为正MM向下凸出为正MM §2.5梁的内力——剪力与弯矩剪力和弯矩的正负号规则：左上右下为正FFlnFsnFsFFsFMFl向下凸为正MMMFsF本例中的剪力和弯矩均为负值 §2.5梁的内力——剪力与弯矩3m2m例题1n5kN解：(1)求支座反力：nMB0RA2kN5mRaRABR5520-=A假设剪力和弯矩为(2)取出脱离体：取正号的方向MA0RB3kNMRB5530-=RAFsM0Fy0FR2kNMRaaA2kNmsA §2.5梁的内力——剪力与弯矩3m2m5kNnR2kNAnR3kN5mBM0RAaRBMRaA6kNm假设剪(2)取出脱离体：5kN力和弯M矩为在集中力作用处的截面，取正号不能含糊地说该截面上的剪力是多大，而应该说RAFs的方向“集中力作用处的左邻截Fy0FRsA50面和右邻截面的剪力各为多大”F3kNs §2.5梁的内力——剪力与弯矩3m2m例题2n5kNm解：(1)求支座反力：nMB0R5505mARRABRA1kN假设剪力和弯矩为(2)取出脱离体：取正号的方向MA0R550BMR1kNBRAFsM0Fy0MR33AkNmFRsA1kN §2.5梁的内力——剪力与弯矩3m2mMRA1kN5kNmnR1kNBnRFB5msRRBAFR0F1(kN)假设剪力和弯矩为sBs(2)取出脱离体：取正号的方向MRB20M2kNm5kNmM在集中力偶作用处的截面，F不能含糊地说该截面上的RsA弯矩是多大，Fy0FR1kNsA而应该说“力偶作用处的左邻截面和右邻截面的弯M0RMA350矩各为多大”M2kN.m §2.5梁的内力——剪力与弯矩例题3F=20kN2解：(1)求支座反力：F=3kN112MB0RA14kNA1m121.5mBFRF863012A2m3m3mRRMA0RB9kNABFM1FFR2360112BF11kNs1(2)取脱离体，求内力RAFs1M1=5kNmF0yFFRsA11-011M2M0FM1131R0AF9kNs2FRBFy0FRsB10s2M2=13.5kNm22M0MR2B150. §2.5梁的内力——剪力与弯矩例题4：求1-1、2-2两截面的内力解：(1)求支座反力：F=2kN1q=1.5KN/mMB0RA55kN.12.25R415420A1A2BMA0RB25.kN1m2m2m.RB41542210RRBA(2)取脱离体，求内力FM11Mq=1.5KN/mFy0Fs12kN211Fs1M0M12kNmFs2RBFy0Fs225152..Fs205kN.22M=2kNmM0M21521252..2 §2.5梁的内力——剪力与弯矩例题4：求1-1、2-2两截面的内力解：(1)求支座反力：F=2KN1q=1.5KN/mMB0RA55kN.12.25R415420AA12BMA0RB25.kN1m2m2m.RB41542210RRAB(2)取脱离体，求内力F1FM1s1F35kNFy0FsA11FRs1.R11AM0M12kNm在集中力作用处的截面，不能含糊地说该截面上的剪力是多大，而应该说“集中力作用处的左邻截面和右邻截面的剪力各为多大” 哈尔滨工业大学本科生课小结(要点)1.求指定截面上的内力时，既可取梁的左段为脱离体，也可取右段为脱离体。一般取外力比较简单的一段进行分析。2.在解题时，一般假设截面上的内力（Fs、M）为正号。3.集中力作用的截面上剪力有突变，其突变的值就是这个集中力的大小；集中力偶作用的截面上弯矩有突变，其突变的值就是这个集中力偶的大小． 哈尔滨工业大学本科生课作业教材第2章后习题(41‐43页)2.4(a)2.5(b)、(e)2.6(d)