材料力学课件5.pdf

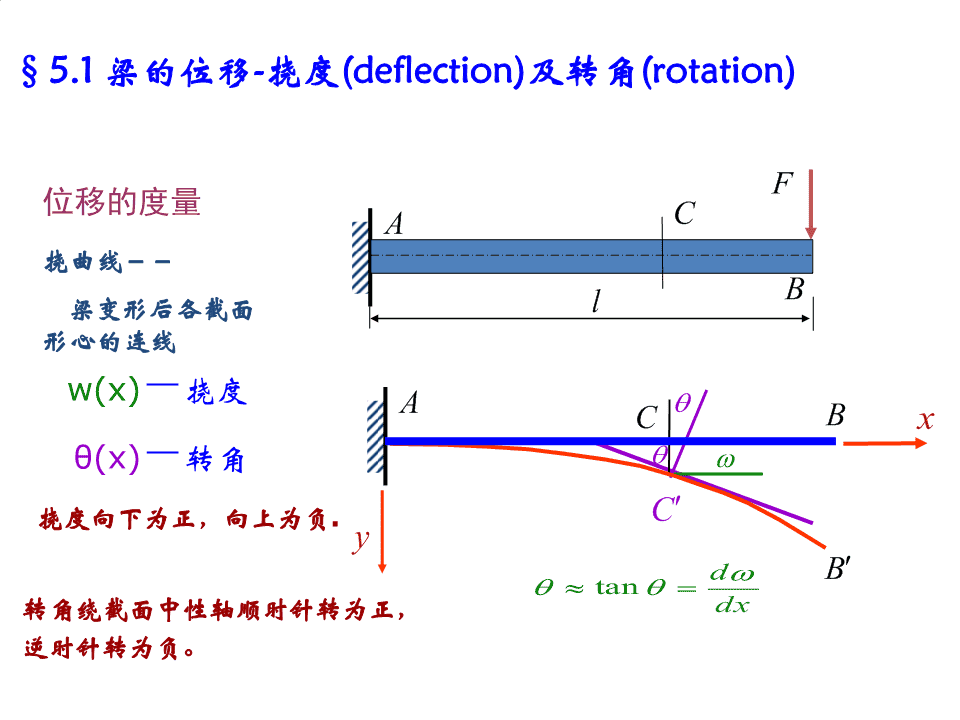
第五章梁弯曲时的位移Chapter5DeflectionsofBeams §5-1梁的位移-挠度及转角§5-2梁的挠曲线近似微分方程及积分§5-3按叠加原理计算梁的挠度和转角§5-5梁的刚度校核及提高刚度的措施§5-6梁的弯曲应变能 §5.1梁的位移-挠度(deflection)及转角(rotation)F位移的度量CA挠曲线－－B梁变形后各截面l形心的连线w(x)－挠度ABCxθ(x)－转角挠度向下为正，向上为负.CydBtan转角绕截面中性轴顺时针转为正，dx逆时针转为负。 §5.2梁的挠曲线近似微分方程及积分2d1M(x)dx2M(x)(x)EI3EIZZd21()dx2d21dx213d221(dx)dM(x)2dxEIZ 2dM(x)2dxEIZoxoxMMMM22dydy0022dxdxyy2dM(x)梁挠曲线近似微分方程2dxEIZ ABCx2dM(x)2dxEICZyBdM(x)dxC1dxEIZM(x)dxdxCxC12EIZ通过积分求弯曲位移的特征：1、适用于细长梁在线弹性范围内、小变形情况下的对称弯曲。2、积分应遍及全梁。在梁的弯矩方程或弯曲刚度不连续处，其挠曲线的近似微分方程应分段列出，并相应地分段积分。3、积分常数由位移边界条件确定。 积分常数C、C由边界条件确定12Xx0xL00Xyx000y 例题5.1求图所示悬臂梁A端的挠度与转角。FxMxFxBAxAA2lFxEICz123FxEICxCz12y6边界条件2FLxL0C1Fx2FL2B2EIz3FL2EI2EIxLB0Czz23EIz3323FL2FLFxFLFLx0xAA2EIz3EIz6EIz2EIz3EIz 例题5.2求图示简支梁在集中荷载F的作用下（F力在右半跨）的最大挠度。FabFbMxx0xax1ABLCFbMxxFxaFbl2FaLaxLLLxFb2AC段EIxCyxz112LFb3EIxCxD边界条件z1116LxLL0CB段Fb212x000EIz2xFxaC22L2连续条件Fb313xaaaEIz2xFxaC2xD2126L6aa1222Fb212FbLbFbFbL2b2EIxFxa2z2EIx2L26Lz1222L62L2Fb313FbLbFb3FbLbEIxFxaxEIxxz2z16L66L6L6L 例题5.3画出挠曲线大致形状。图中C为中间铰。FA两根梁由中间铰连接，挠曲线在中间铰处，挠度连续，但转角不连续。1212 例题5.4用积分法求图示各梁挠曲线方程时,试问下列各梁的挠曲线近似微分方程应分几段;将分别出现几个积分常数,并写出其确定积分常数的边界条件挠曲线方程应分两段AB,BC.F共有四个积分常数qx边界条件ACBEIzaLxaB0xaLC0y连续条件xaB1B2B1B2 §5.3按叠加原理计算梁的挠度和转角叠加法计算位移的条件：1、梁在荷载作用下产生的变形是微小的；2、材料在线弹性范围内工作，梁的位移与荷载呈线性关系；3、梁上每个荷载引起的位移，不受其他荷载的影响。 例题5.4试用叠加原理求图示弯曲刚度为EI的简支梁的跨中z截面挠度ω和梁端截面的转角θθ.cABFqBcqcFcA5qL43CEIzFLqc384EIFcl2l2z48EIz43q5qLFLcB384EIz48EIzACEIzl2l2AqAFA32qLFLFqAFA24EI16EIzzBAEICz32qLFLABl2l224EI16EIzz 例题5.5变截面梁如图示，试用叠加法求自由端的挠度ω.c3FLF2C1EIz1EI3EIz2z2ALBLCC2BFBM1232FLFL11FBFBF3EI2EIz1z1BC2FLLFL2L121BMBMF2EIz1EIz1MFL2LACC3BFBM2B23222FL2FL1FL2L1FL1L2FL2L1C3C1C2C33EIz23EIz12EIz12EIz1EIz1 例题5.6悬臂梁受力如图示.关于梁的挠曲线,由四种答案,请分析判断,哪一个是正确的?MMMeMeeeAABCDl2Bl2Cl2Dl2l2l2(a)MeMeMeMeAABCDBCDl2l2l2l2l2l2(b)(C)MeMeAB,CD段弯矩为零，所以这两段保持直ABCD线不发生弯曲变形。AB,BC,CD三段变l2l2l2形曲线在交界处应有共切线。(d) §5.5梁的刚度校核.提高梁的刚度的措施I.梁的刚度校核maxllmax 例题5.7悬臂梁承受荷载如图示。已知均布荷载集度q=15kN/m，梁的长度L=2a=2m，材料的弹性模量E=210GPa，许用正应力[σ]=160MPa，梁的许可挠度[ω/L]=1/500。试选择工字钢的型号。qC1.按强度选择ABL2a2L2aMmax3qa3W140.6cm2查表：选16号工字钢43I1130cm,W141cmzz 2.按刚度选择4q41qamaxB1B2B324EIZCAB44q2a2qaL2aL2aB18EIEIZZ4qaB2Cqq8EIZ34qaqaABB3CaaC6EIZ6EIZL2aL2a3max41qa1I3050cm4L48EIL500ZZ查表：选22号工字钢ABaC43I3400cm,W309cmqzz II.提高刚度的途径提高刚度主要是指减小梁的弹性位移弹性位移不仅与载荷2dM(x)有关，而且与杆长和2dxEIZ梁的弯曲刚度(EI)有Z关改变增加减小改变改变荷载支座梁的梁的材料类型长度截面形状 §5.6梁内的弯曲应变能假设微段发生纯弯曲11dxMx()Mx()dWMM222dx1dMMxMxd22EIEIzzMe2MxVWddWxMeLL2EIZO