材料力学课件7.拉压应力.pdf

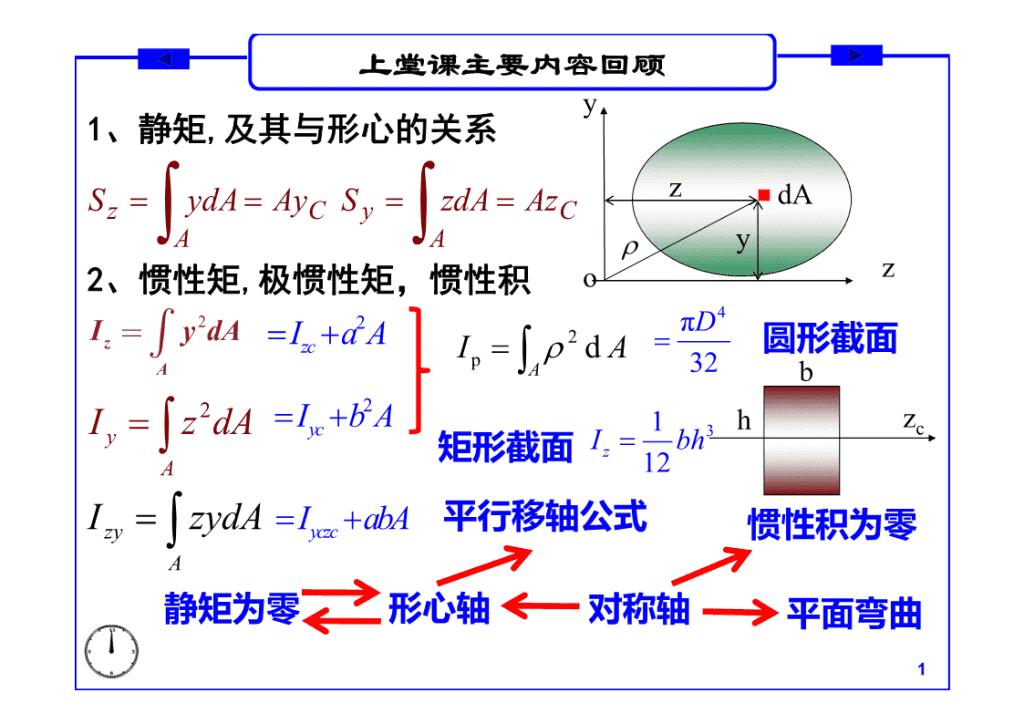
上堂课主要内容回顾y1、静矩,及其与形心的关系zdASzydAAyCSyzdAAzCAAy2、惯性矩,极惯性矩，惯性积oz4I=ydA22πDzòIzcaAI2dA圆形截面ApA32b2IbA2IzdAyc13hzcy矩形截面IbhzA12IzyzydAIyczcabA平行移轴公式惯性积为零A静矩为零形心轴对称轴平面弯曲1 哈尔滨工业大学本科生课第4章应力计算及强度条件§4.1轴向拉压杆横截面及斜截面上的应力 前情回顾：应力为什么要讨论应力?1.FFFF2.通常情况下，同一截面各个点上内力是不相同的。需要知道截面上哪个点处最危险，研究内力在截面上各点的分布情况。应力的概念①应力定义：截面上一点处内力的密集程度是反映一点处内力的强弱程度的基本量 前情回顾：应力②指定截面上、一点的全应力或总应力：pτFdFplimαA0AdAσ③垂直于截面的应力分量----正应力FdFNNlimA0AdAFdFss④切于截面的应力分量------切应力limA0AdA222p,,三者之间的关系：p22⑤应力的单位：牛顿/米(N/m)，或帕(Pa)。1Mpa(兆帕）=106Pa,1GPa（吉帕）=109Pa。 前情回顾：应力应力计算公式的推导思路：实验由实验现象→变形规律做一些合理的假设→应变规律利用胡克定律→应力分布规律→应力计算公式1.变形几何条件2.物理条件，应力应变关系（本构关系）3.静力学条件 前情回顾：应力在正应力作用下，单元体棱边的长度发生改变。产生——线应变（正应变）pτα拉压胡克定律Eσ 前情回顾：应力pτ在切应力作用下，棱边的夹角发生改变。α——角应变（切应变）σ剪切胡克定律G 哈尔滨工业大学本科生课§4.1轴向拉压杆横截面及斜截面应力 §4.1轴向拉压杆横截面及斜截面应力4.1.1轴向拉压杆横截面的应力推导思路：实验→变形规律→总结应变规律→应力分布规律→应力计算公式1、实验：变形前受力后FF2、变形规律：横向线——仍为平行的直线，且间距增大。纵向线——仍为平行的直线，且间距减小。3、平面假设：变形前垂直轴线的横截面，变形后仍为垂直于轴线的平面 §4.1轴向拉压杆横截面及斜截面应力4.1.1轴向拉压杆横截面的应力平面假设3、平面假设：变形前垂直轴线的横截面，变形后仍为垂直于轴线的平面（横截面相对轴线平移） §4.1轴向拉压杆横截面及斜截面应力4、应力的分布规律——内力沿横截面均匀分布拉压胡克定律EF5、应力的计算公式：FNFNAFNA——轴向拉压杆横截面上正应力的计算公式NN2Pa2MPammm §4.1轴向拉压杆横截面及斜截面应力6、拉压杆内最大的正应力：FFNmaxN等直杆：max变直杆：maxAAmax7、正应力的符号规定——同内力拉应力为正值，方向背离所在截面。压应力为负值，方向指向所在截面。8、公式的使用条件(1)轴向拉压杆(2)除外力作用点附近以外其它各点处。 §4.1轴向拉压杆横截面及斜截面应力外力的等效圣维南原理F作用于杆上的外力可以用其等效力系代替，F/2但替换后外力作用点附F/2近的应力分布将产生显著影响，且分布复杂，F/3其影响范围不超过杆件F/3的横向尺寸。F/3外力对内力的影响区域 §4.1轴向拉压杆横截面及斜截面应力4.1.2轴向拉压杆任意斜面上应力的计算1、斜截面上应力确定FF(1)内力确定：F=FNFx(2)应力确定：FN①应力分布——均布FpFN②应力公式——FFFpNcoscosAAAcos §4.1轴向拉压杆横截面及斜截面应力FNFFpcoscosAAAcos2Fpcoscosppsinsin222、符号规定⑴、：斜截面外法线与x轴的夹角。由x 轴逆时针转到斜截面外法线——“”为正值；由x 轴顺时针转到斜截面外法线——“”为负值⑵、σ：同“σ”的符号规定⑶、τ：在保留段内任取一点，如果“τ”对该点之矩为顺时针方向，则规定为正值，反之为负值。 §4.1轴向拉压杆横截面及斜截面应力3、斜截面上最大应力值的确定FxFNcos2,sin22(1):max0,max,横截面上。(0)(2):maxmax0245,450斜截面上。()2 §4.1轴向拉压杆横截面及斜截面应力 §4.1轴向拉压杆横截面及斜截面应力4.1.3拉压杆的强度计算1、极限应力、许用应力⑴、极限应力（危险应力、失效应力）：材料发生破坏或产生过大变形而不能安全工作时的最小应力值。σu（a）给构件足够的安全储备。考虑到：（b）理论与实际的差异。⑵、许用应力：构件安全工作时的最大应力。“[σ]”u（其中n为安全系数,值＞1）n §4.1轴向拉压杆横截面及斜截面应力2、强度条件：最大工作应力小于等于许用应力≤maxF等直杆：NmaxmaxAFN变直杆：maxAmax §4.1轴向拉压杆横截面及斜截面应力3、强度条件的应用：（解决三类问题）：（1）校核强度——已知：F、A、[σ]。求：max≤？解：FNmaxmax？A（2）设计截面尺寸——已知：F、[σ]。求：AF解：NmaxmaxA≥FNmax／[σ]。A（3）确定外荷载——已知：[σ]、A。求：F。解：FNmaxmaxAF≤[σ]A。→FNmax §4.1轴向拉压杆横截面及斜截面应力例1已知一圆杆受拉力F=25kN，直径d=14mm，许用应力[]=170MPa，试校核此杆是否满足强度要求(校核强度)。FFF25KNNX解：1、轴力F=F=25kNN3F4F42510N162MPa2、应力：max22Ad3.140.0143、强度校核：max162MPa170MPa此杆满足强度要求，能够正常工作。 §4.1轴向拉压杆横截面及斜截面应力3mB例2已知钢杆AB为圆杆,直径d=25mm,A[σ]=140MPa,木杆BC为正方形,边长为钢2ma=100mm,[σ]木=10MPa,F=50kN.试校核支架强度.FC解:1.内力分析22F32Fk5090.1N（压）NBCFFsin23Ncos90.175ABFFkNNNABBC2232（拉）2.强度条件FNBCF90.1103NBC9.01MPa[]木木22a0.1木杆满足强度要求F3N75104AB152.8MPa[]钢杆不满足强度要求钢22钢d/40.025 §4.1轴向拉压杆横截面及斜截面应力3mB例2已知钢杆AB为圆杆,直径d=25mm,A[σ]=140MPa,木杆BC为正方形,边长为钢2ma=100mm,[σ]木=10MPa,F=50kN.试校核支架强度.FC解:1.内力分析2.强度条件3.重新选择钢杆截面d2FFk75N（压）NABNAB[]A钢4[]F钢FN3AB4FN47510dmAB＝＝26.12m6[]14010钢FNBC取＝dm27m §4.1轴向拉压杆横截面及斜截面应力例3已知：l,h,F（0