材料力学课件4

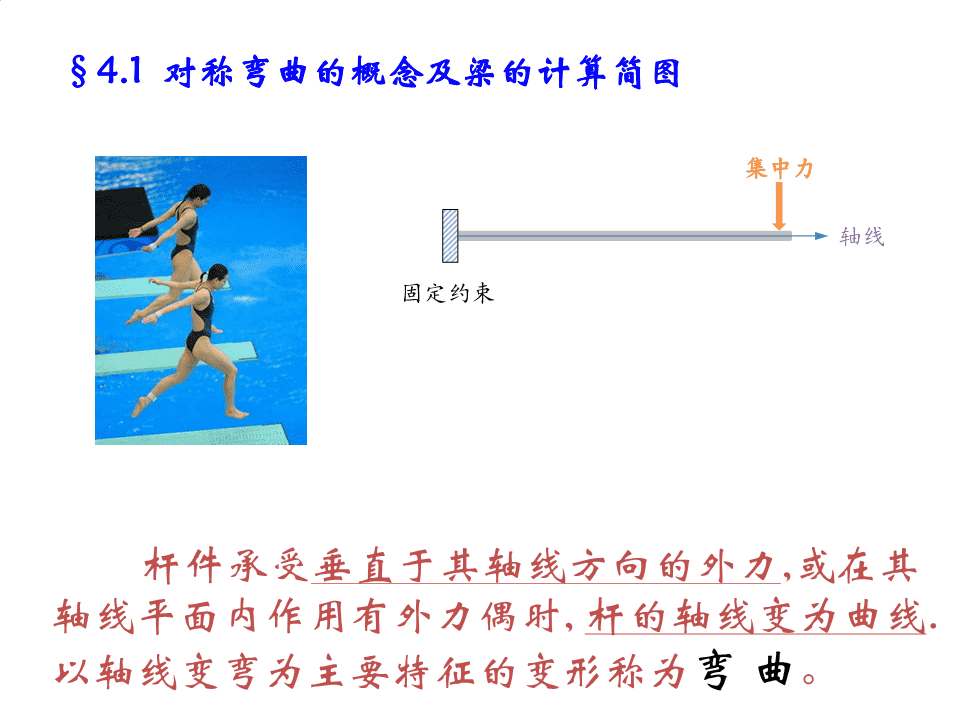
第四章弯曲应力Chapter4StressinBending §4-1对称弯曲的概念及梁的计算简图§4-2梁的剪力和弯矩—剪力图和弯矩图§4-3平面刚架和曲杆的内力图§4-4梁横截面上的正应力—正应力强度条件§4-5梁横截面上的切应力—切应力强度条件§4-6梁的合理设计 §4.1对称弯曲的概念及梁的计算简图集中力轴线固定约束杆件承受垂直于其轴线方向的外力,或在其轴线平面内作用有外力偶时,杆的轴线变为曲线.以轴线变弯为主要特征的变形称为弯曲。 FF21力学模型y杆轴XFFzAB形心纵向对称面构件几何特征构件为具有纵对称面的等截面直杆受力特征横向外力（或外力合力）或外力偶均作用在杆的纵向对称面内变形特征杆件轴线变形后为外力作用面内的平面曲线，或任意两横截面间绕垂直于外力作用面的某一横向轴作相对转动 FF2对称弯曲1构件的几何形状、材料性能和外力作用均对称于杆件的纵对称面杆轴X平面弯曲FF梁变形后的轴线所在平面与外力所在平面AB相重合纵向对称面qMFe纵向对称弯曲必定是平面弯对称面曲，而平面弯曲不一定是对称弯曲。BAx非对称弯曲FAyFBy构件不具有纵对称面，或y虽有纵对称面但外力不作用在纵对称面时的弯曲变形 梁：以弯曲变形为主的杆件静定梁支座反力可以由静力平衡方程求解的梁超静定梁支座反力仅由静力平衡方程不能求解的梁墙楼板梁ql 梁按支承方法的分类悬臂梁3（2）简支梁3（2）外伸梁3（2）固定梁6（4）连续梁4（3）半固定梁4（3） 作用在梁上的载荷形式分布荷载集中力Me均匀分布荷载集中力偶 §4.2梁的剪力和弯矩.剪力图和弯矩图I.剪力和弯矩FaFFSAABFAFlBMFxAMFAxFs 符F＞0F＜0ss号规定：M＞0M＜0使微段梁有顺时针转动趋势的剪力为正，反之为负；使微段梁产生向下凸变形的弯矩为正，反之为负。 4.1试确定截面C及截面D上的剪力和弯矩例题2FlFFFFMFlACsCABCDllMFlFFCCsMAFFCsM2FlFl0ACACMlCFFDsM2FlAFFCsM0DMBCCDFlFDsMDBD 截开后取左边为示力对象：向上的外力引起正剪力，向下的外力引起负剪力；向上的外力引起正弯矩，向下的外力引起负弯矩；顺时针引起正弯矩，逆时针引起负弯矩。截开后取右边为示力对象：向上的外力引起负剪力，向下的外力引起正剪力；向上的外力引起正弯矩，向下的外力引起负弯矩；顺时针引起负弯矩，逆时针引起正弯矩。 例题求图示外伸梁中的A、B、C、D、E、F、G4.2各截面上的内力。2kNm6kNm3kN1kNmCADEFBGFAFB1m1m1m1m1m1m1m1m 例题4.3求图示外伸梁中的1－1、2－2、3－3、4－4和5－5各截面上的内力6kNm6kN12345q2kNmB12345AC2m3m3mFA13kNFB5kN 例题一长为2m的均质木料，欲锯下0.6m长的一段。为使在锯4.4开处两端面的开裂最小，应使锯口处的弯矩为零，木料放在两只锯木架上，一只锯木架放置在木料的一端，试问另一只锯木架放置何处才能使木料锯口处的弯矩为零。q2q1xAMD0FACDB2xx2laMFlaq0a0.6mCAl2m222q1x1.41.4q0x0.462m2x2 II剪力方程和弯矩方程--剪力图和弯矩图剪力方程和弯矩方程：剪力和弯q矩沿轴线的变化规律qlABFqxSx2FAlFB2qlqxMxql222ql剪力图：正剪力的画在上方2弯矩图：正弯矩的画在下方2ql8 例题图示悬臂梁AB,自由端受力F的作用,试作剪力4.5图和弯矩图.FFxF0xLSAXBlMxFx0xLkNFFLkNm 例题图示外伸梁,,试作剪力图和弯矩图.4.640kNm10kNm20kNFx20kNS1X1AX2B0x111m35kN4m25kNMx20x11152.50x11FSx22510x2kN0x2420225x2Mx25x10222020x422031.25kNm III分布荷载集度、剪力和弯矩间的微分关系及其应用ymnmnM(x)M(x)dM(x)xF(x)dF(x)FxSSsmnmnq(x)xdxdxdFsqFqxdxFdF0dxsss2dMqxdxFMFdxMdM0SSdx2 2dFdMdMsqFqS2dxdxdxdFsFC剪力图是水平直线.0SdxdMC弯矩图是斜直线.dxdM0MC弯矩图是水平直线.dxdFsq剪力图是斜直线.弯矩图是二次抛物线.0dx 例题4.7qACDBacbFFABlF+A-FxB+FaFBbA 例题4.82kNmFFaaa4m3kN5FkNkN34Fa2.25kNmkNm 突变规律(从左向右画)1、集中力作用处，F图突变，方S向、大小与力同；M图斜率突变，突变成的尖角与集中力F的箭头是同向。2、集中力偶作用处，M图发生突变，顺下逆上，大小与M同，F图不发生变化。S 例题4.9作图示梁的内力图3kN4.5kNm2kNmDACBEFA10kNFB2kN1m2m2m1m7kN3x1.56232kNm22.44 例题4.106kN2kNm4kNm1m1m2m4.5kN1.55.54kNm8.57 例题160kN40kNm40kN80kNm4.11CADEBF130kN310kN1m1m2m4m2m13012040kN30190160kNm130210280340 32qMqa21FqaD4AaBaCaD32FMqa7B’q2FFqaABM4AFBBCaDa72MqaAA4aFD1F7qaAqa44kN752qaqa4412qa321272qa例题qa4kNm44.12 例题叠加法作弯矩图4.13FFqq＋ABABABlllFFqLF+qL1/2qL2+FL21/2qLFL 例题q4.14BAqaqqa2aa2结构对称，qaqa22载荷反对称，qaa2a222则F图对称，qaS8M图反对称2qa8 FF例题AB4.15FF2F2aaaaF2F2F2F2Fa2Fa2结构对称，载荷对称，则F图反对称，SM图对称 §4.3平面刚架和曲杆的内力图刚架：由两根或两根以上的杆件组成的并在连接处采用刚性连接的结构。当杆件变形时，两杆连接处保持刚性，横梁即角度（一般为直角）保持不变。立柱在平面载荷作用下，组成刚架的杆件横截面上一般存在轴力、剪力和弯矩三个内力分量。 例题求做图示刚架的内力图4.16BCqLL2qqL/2LF(kN)sqLAqL2qLqL/222qL2FN(kN)M(kNm)qL2 例题求做图示刚架的内力图4.172kNB2C4m4mF(kN)s2kN/m8kN8A24kNm2kN88M(kNm)F(kN)N242 例题等截面折杆ABC的A端固定在墙上,自由端承受集4.18中力F=20kN.设L1=2m,L2=1m,θ1=450,θ=900,试作折杆的剪力和弯矩图214.1414.14A114.14214.1414.14kN14.1414.14kNFM(kNm)F(kN)s 例题图示杆ABC由直杆和半圆组成,试作该杆的内4.19力图.FrFrBCFM(kNm)2rF(kN)sA2FrAB:M2FrFFNF0SFBC:MFr1cosF(kN)NFFcosNFFsinSF §4.4梁横截面上的正应力.梁的正应力条件I.纯弯曲时梁横截面上的正应力FFaaACDB纯弯曲：梁受力弯曲后，如F其横截面上只有弯矩而无剪力，F这种弯曲称为纯弯曲。Fa 实验现象：1、变形前互相平行的纵向直线、FF变形后变成弧线，且凹边纤维缩mn短、凸边纤维伸长。2、变形前垂直于纵向线的横向mn线,变形后仍为直线，且仍与弯曲了的纵向线正交，但两条横向线间相对转动了一个角度。平面假设：变形前杆件的横截面变形后仍为平面。中性层mn中性轴：中性层与横截面的交线称o1为中性轴。o2中性轴mn FFmnyddydmnyEEMM中性轴EzFdAydA0nyNAAmoEoMyAzdAzydA0AdAzE2EIZmndMzAydAydAyAdx1MZMyzdxEIZIyzy M:横截面上的弯矩MM中性轴Zzmnyy:到中性轴的距离ooIdAZ:截面对中性轴的惯性矩zmnydxMMMyzIzMzmaxWz中性轴 II.纯弯曲理论的推广纯弯曲横力弯曲只有弯矩有弯矩和剪力正应力正应力、切应力、层间挤压应力Mz推广Mx()zmaxWmaxzlh/5WzEulerBeam 例题长为l的矩形截面悬臂梁，在自由端作用一集中力F，4.20已知b＝120mm，h＝180mm、l＝2m，F＝1.6kN，试求B截面上a、b、c各点的正应力。h6aFABCbhl2l2h2FLcb31bhMFLI1hBZ212FLMBya231.65MPaa3IbhZ121hFLMByc222.47MPa（压）b0c3IbhZ12 例题试计算图示简支矩形截面木梁平放与竖放时的最大正4.21应力，并加以比较。q2kNm1002002004m100竖放2qLMmax86MPamax2WbhZqL26横放82qLMmax812MPamax2WhbZ6 例题4.22图示T形截面简支梁在中点承受集中力F＝32kN，梁的长度L＝2m。T形截面的形心坐标y＝96.4mm，横截面对于z轴的惯性矩I＝1.02×108mm4。求cz弯矩最大截面上的最大拉应力和最大压应力。yF150AB5096.4llz200C22FL50M16kNmmax4Mymax24.09MPamaxIymax2005096.4153.6mmZMyy96.4mmmaxmax15.12MPamaxIZ III.梁的正应力强度条件MyMmax对梁的某一截面：maxIzWZMyM对全梁（等截面）：maxmaxmaxmaxIzWzMmaxmaxWz 例题长为2.5m的工字钢外伸梁，如图示，其外伸部分为0.5m，梁上承受均布荷载，q=30kN/m，试选择工字钢型号。已知工字钢抗弯强4.23度［σ］=215MPa。q30kNmMWmax3Z61.2cmBA0.5m2m查表F46.9kNFB28.1kNA31.9N12.6工字钢W=77.5cm30ZkN1528.13.75kNm13.16 例题铸铁梁受荷载情况如图示。已知截面对形心轴的惯性矩I=403×10－7m4，铸铁抗拉强度［σ＋］=50MPa，抗压强度4.24z［σ－］=125MPa。试按正应力强度条件校核梁的强度。200F25kNq12kNm3061ACBDz1701m3m2m13924B截面33032410611036.3MPaBmax74031012.75kNm3324101391082.8MPaC截面Bmax7403103312.75101391044MPaCmax740310如果T截面倒置会如何??? 例题铸铁制作的悬臂梁，尺寸及受力如图示，图中F＝20kN。梁的截面为T字形，形心坐标y=96.4mm。已知材料的拉伸许用应力和4.25c压缩许用应力分别为[σ]+＝40MPa，[σ]－＝100MPa。试校核梁的强度是否安全。yFABC150BA5096.42F1400600z20012kNm50MAyl24.09MPaAIZ16kNmMAyyMByy18.07MPaA15.12MPaBIIZZ 例题为了起吊重量为F＝300kN的大型设备，采用一台150kN和一台200kN的吊车，以及一根工字形轧制型钢作为辅助梁，组成临时的4.26附加悬挂系统，如图示。如果已知辅助梁的长度l=4m，型钢材料的许用应力[σ]＝160MPa，试计算：1.F加在辅助梁的什么位置，才能保证两台吊车都不超载？2.辅助梁应该选择多大型号的工字钢？200kN吊车150kN吊车1.确定F加在辅助梁的位置MA0FBlFlx0FlxBFPABC辅助梁lFAxFBM0FxFl0BAFFxFAllFxFlx令:F200kNFB150kNAll2x2.667x2.667mx2m 200kN吊车150kN吊车2.确定工字钢型号ABMA200l2.667266.6kNmmaxC辅助梁xFFABMB1502300kNmFmaxMBlmaxmaxWzMmaxB33W1.87510cmZ1.8751.86100％0.8％1.875 例题4.27图示结构承受均布载荷，AC为10号工字钢梁，B处用直径d=20mm的钢杆BD悬吊，梁和杆的许用应力[σ]＝160MPa。不考虑切应力，试计算结构的许可载荷[q]。3q9qFDFAkNBkNd44qFB梁的强度AM0.5qmaxBCWWZZFA2m1mWZq15.68kN/m1q0.52杆的强度9q9qF4NBD1232Ad412qd22.3kN/mq15.68kN/m9 例题简支梁如图所示，试求梁的最底层纤维的总伸长。4.28qABhxdxlbM(x)解：1、计算梁底层微段的伸长量(x)(x)E(x)W11Z2M(x)qlxqx3q(dx)(x)22(lxx2)(x)EWbh2Ebh2dxZE63q2(dx)(lxx)dx2Ebh2、梁的最底层纤维的总伸长3l3ql2l3lqll(dx)2(xx)20Ebh2302Ebh 承受相同弯矩M的三根直梁，其截面组成方式如图所示。图（a）的截例题z面为一整体；图（b）的截面由两矩形截面并列而成（未粘接）；图4.29（c）的截面有两矩形截面上下叠合而成（未粘接）。三根梁中的最大正应力分别为σ（a）、σ（b）、σ（c）。关于三者之间的maxmaxmax关系有四种答案，试判断哪一种是正确的。dz(A)(a)(b)(c)；zz2maxmaxmaxddzd2(B)(a)(b)(c)；ddmaxmaxmaxd22d(a)(b)(c)(C)(a)(b)(c)；Mzmaxmaxmax(a)Mz6Mz26Mzmaxd3d3max(b)3d2d(D)(a)(b)(c)。6.dmaxmaxmax26Mz12M(c)2zmax23Bddd26 §4.5梁横截面上的切应力.梁的切应力强度条件q横力弯曲FFRRkNkNm I.矩形截面梁的切应力y假设：Fs1、横截面上的τ方向与F平行Sz2、τ沿截面宽度是均匀分布的 F122hzaayyy21ayah12xdAdxyA12byMMdMFN1FN2aa*FSsz**12FN2FN1ybdx0IzbbMyMF*dA1dAydAdxN1*1*A*1AAIIzSzz*dMSdM*MdMyydAbdxzFdA1dA*1yyN2A*2*IAAIzIbdxzz *FsSzF–横截面上的剪力；S＊–宽度线一侧的面积对中性轴的静矩.sZIzbb–截面的宽度；IZ–截面对中性轴的惯性矩；b2hFh2zmaxs2y(y)yy2I420ZhAy22FshFsh3Fsmax38Ibh2AZ812 例题矩形截面简支梁，加载于梁中点C，如图示。4.30求σ,τ。maxmaxFL2FbhMmaxWZh46l2l2FLbM43FLmaxmax12W22bhFZbhF6smax23FLF2bh22L3F323Fmaxsmax3Fh2A2bh4bhmax4bhL细长等值梁5max10hmax II.工字形截面梁的切应力*FSszdIdZ0zhhmaxtminbF222Sbhh0dh02横截面上的切应力(95--97)％IdyZ24424由腹板承担,而翼缘仅承担了(3--5)％,且翼缘上的切应力情况又比较222复杂.为了满足实际工程中计算和FSbhbh0dh0设计的需要仅分析腹板上的切应maxId888Z力.I22ZFbhbhS0*minSZmaxIZd88 III.圆形和圆环形截面梁的最大切应力DddzyF4FSS2maxmaxA3A2dA4A为圆环形截面面积 例题如图所示倒T型外伸梁，已知q=3kN/m，F1=12kN，F2=18kN，形心主惯性矩I=39800cm4。（1）试求梁的最大拉应力和最大压应力及其所在的位置；4.31Z（2）若该梁是由两个矩形截面的厚板条沿图示截面上的ab线（实际是一水平面）胶合而成，为了保证该梁的胶合连接强度，水平接合面上的许用切应力值是多少？80FFq12BB300ABCDz3m343m6m14ab148.550224200最大拉应力发生在B截面上1214S*20050148.525最大压应力发生在F=0的截面上36Zs33123510mm16.5MPa15MPaab线上最大切应力发生在BC段3032.680.85MPa0.34MPaab2ab1FS*0.85MPaSZ333322101235102210123510IZbab1-4ab2-43980010803980010200 IV.梁的切应力强度条件*FSSZIbZ最大正应力发生在最大弯矩截面的上、下边缘处，该处的切应力为零，即正应力危险点处于单轴应力状态；最大切应力通常发生在最大剪力截面的中性轴处，该处的正应力为零，即切应力危险点处于纯剪切应力状态； 例题两个尺寸完全相同的矩形截面梁叠加在一起承受荷载如图示,若材料许用应力为[σ],其许可荷载[F]为多少?如将两根梁用一个螺栓联成一整体,则4.32其许可荷载[F]为多少?若螺栓材料许用切应力为[τ],求螺栓的最小直径.F3FL两梁叠加:2bhzMmaxFLmax2h2Wbhzz2b62LbhFmax3L两梁用螺栓连接两梁只有一个中性轴2将两个梁连接MFL2bhmaxF成一个整体后,承max2Wzb2h3L载能力提高一倍.梁中性层处切应力6中性层剪力hb2Fs22bhFbLAd2smax3Fs33Lhmax42A22bh2Ld2hb §4.6梁的合理设计一、合理选择截面形状，尽量增大W值z1.梁的合理截面29.72cm3hb30.167a263bh3N100.118a49cmO6 工字形、槽形截面比矩形截面合理，矩形截面比圆形截面合理 2.根据材料特性选择截面对于抗拉和抗压不相同的脆性材料最好选用关于中性轴不对称的截面 二、合理布置梁的形式和荷载，以降低最大弯矩值1.合理布置梁的支座qqAABBl0.2l0.6l0.2l220.025ql0.025ql20.125ql20.025ql 2.适当增加梁的支座qqAABBll22ll20.03125ql220.0175ql0.125ql 3.改善荷载的布置情况FqFlll22l+10.125ql2Fl4 三、采用变截面梁 四、合理利用材料混凝土xxx钢筋钢筋混凝土材料在合理使用材料方面是最优越的 (a)(b) 例题矩形截面简支梁由圆形木材刨成，已知F=5kN，4.33a=1.5m，[σ]=10MPa，试确定此矩形截面h/b的最优比值，使其截面的抗弯截面系数具有最大值，并计算所需圆木的最小直径d。FFABCD2、确定圆木直径ddhaaabMmax[]maxW解：1、确定W最大时的h/bZZ222MFa7.5kNmbhb(db)maxWZ66M7.5103Nmmax43WZ7510mmdW[]10106PaZ0dbbh21243W[(2b)b]7510mmb131mm。Z66122h(h2b)022222226bdhb3b51510mm 例题悬臂梁由两根槽钢背靠背(两者之间未作任何固定连接)4.34叠加起来放置,构成如图示.在载荷作用下,横截面上的正应力分布如图_________D所示.FIzI-I剖面zI(A)(B)(C)(D) 例题在图示十字形截面上,剪力为Fs,欲求m--m线上的切4.35*FS应力,则公式中sz,____.DIbZ*yA、S为截面的阴影部分对z轴的静矩，b4；z*B、S为截面的阴影部分对z轴的静矩，b；zmmz*C、S为截面的阴影部分对z轴的静矩，b4；zz*FD、S为截面的阴影部分对z轴的静矩，b；sz4 例题若对称弯曲直梁的弯曲刚度EI沿杆轴为常量,4.36其变形后梁轴_____A.A、为圆弧线，且长度不变。B、为圆弧线，而长度改变。C、不为圆弧线，但长度不变。D、不为圆弧线，且长度改变。