压杆稳定1-同济大学材料力学课件

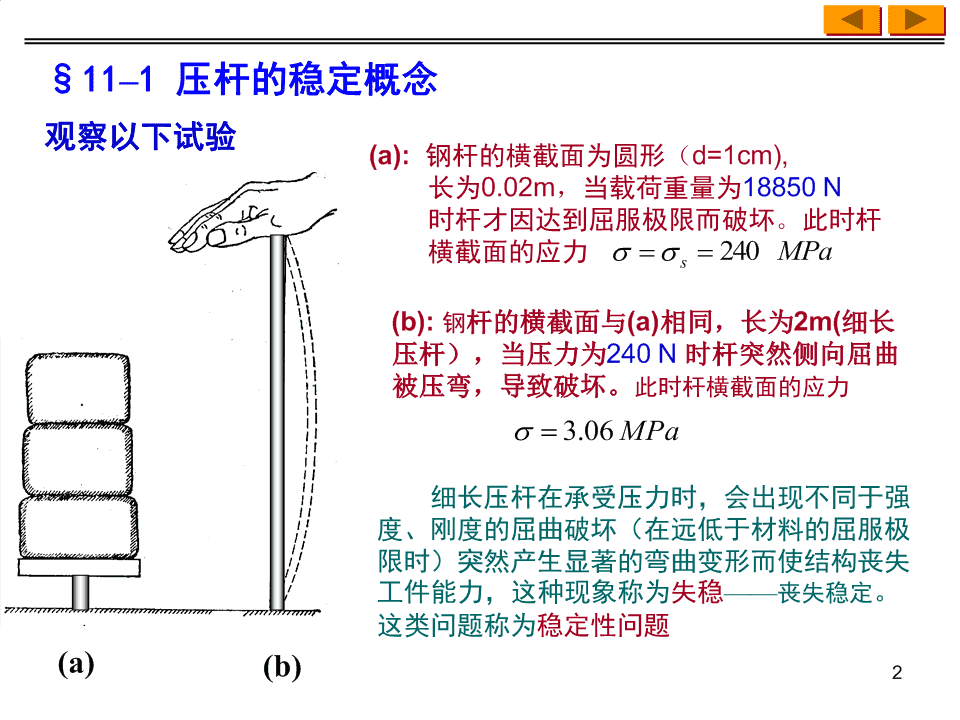
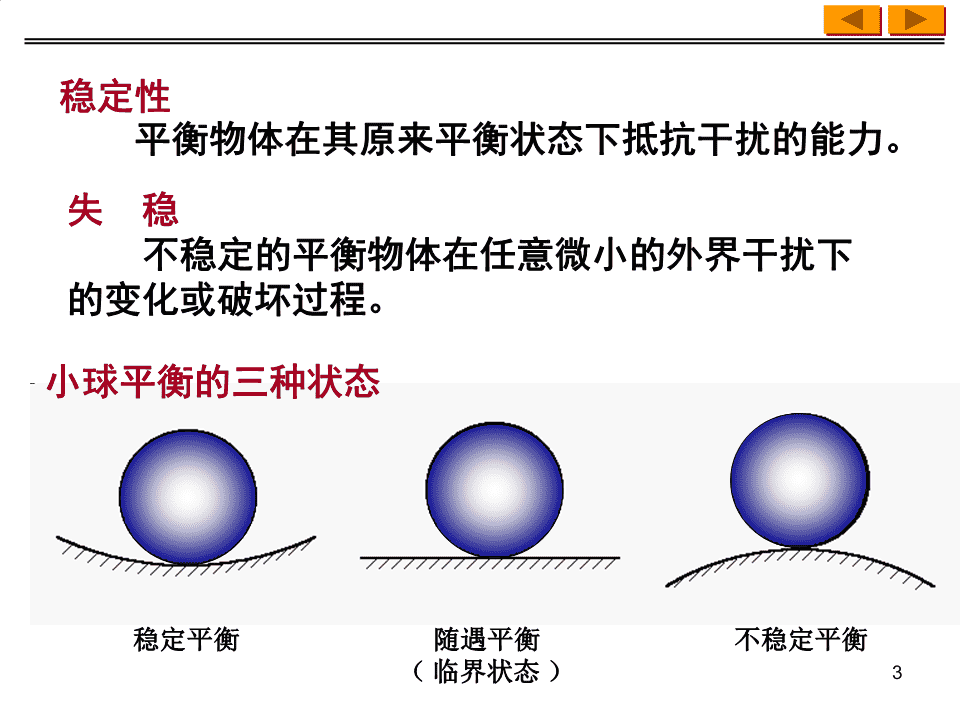
第十一章压杆稳定§11-1压杆的稳定概念§11-2细长压杆临界压力的欧拉公式§11-3欧拉公式的使用范围临界应力总图§11-4压杆的稳定计算§11-5提高压杆稳定性的措施1 §11–1压杆的稳定概念观察以下试验(a):钢杆的横截面为圆形（d=1cm),长为0.02m，当载荷重量为18850N时杆才因达到屈服极限而破坏。此时杆横截面的应力240MPas(b):钢杆的横截面与(a)相同，长为2m(细长压杆），当压力为240N时杆突然侧向屈曲被压弯，导致破坏。此时杆横截面的应力3.06MPa细长压杆在承受压力时，会出现不同于强度、刚度的屈曲破坏（在远低于材料的屈服极限时）突然产生显著的弯曲变形而使结构丧失工件能力，这种现象称为失稳——丧失稳定。这类问题称为稳定性问题(a)(b)2 稳定性平衡物体在其原来平衡状态下抵抗干扰的能力。失稳不稳定的平衡物体在任意微小的外界干扰下的变化或破坏过程。小球平衡的三种状态稳定平衡随遇平衡不稳定平衡（临界状态）3 4 5 6 受压直杆平衡的三种形式稳定平衡随遇平衡不稳定平衡（临界状态）7 8 9 10 工程项目的压杆稳定试验11 三、其它工程结构的失稳现象12 13 薄壁圆管、拱（曲梁）失稳14 压力容器容器在外压力作用下不再保持原平衡状态。外压不仅有强度问内压仅是强度问题题，还有稳定问题。 工程中其他失稳形式：1.板（壳）的压缩或剪切失稳；2.深梁的弯曲失稳；3.薄壁管的压缩局部失稳；4.圆环的外压失稳等。16 §14-2细长压杆的临界压力一、两端铰支细长压杆的临界载荷当达到临界压力时，压杆处于微弯状态下的平衡yFLNLyFcr17 两端铰支细长压杆的临界载荷考察微弯状态下局部压杆的平衡:M(x)=Fcry(x)yd2yM(x)=–EIdx2FLcr2Fcr令kEI2ydy2ky0F2crdx二阶常系数线性齐次微分方程18 两端铰支细长压杆的临界载荷2dy22Fcrky0(k)2EIdx（二阶常系数线性齐次微分方程）y微分方程的解:y=Asinkx+BcoskxFcrL边界条件:y(0)=0,y(l)=00•A+1•B=0sinkl•A+coskl•B=0yFB=0crsinkl•A=0若A=0，则与压杆处于微弯状态的假设不符因此可得：19 考察微弯状态下局部压杆的平衡:M(x)=Fcry(x)d2yyM(x)=–EIdx2Fcr2FcrL令kEI2dy2yky02Fdxcr二阶常系数线性齐次微分方程20 2Fdy20(k2cr)ky2EIdx（二阶常系数线性齐次微分方程）y微分方程的解:y=Asinkx+BcoskxFcrL边界条件:y(0)=0,y(l)=00•A+1•B=0sinkl•A+coskl•B=0yFB=0crsinkl•A=0若A=0，则与压杆处于微弯状态的假设不符因此可得：21 y=Asinkx+BcoskxB=0sinkl•A=0sinkl=0ykln（n=1、2、3……）FN2Fcr由k可得EI22ynEIFcr2Fcrl22 22nEI临界载荷:Fcr2lnxy(x)Asin屈曲位移函数:l临界力F是微弯下的最小压力，cr故取n=1。且杆将绕惯性矩最小的轴弯曲。最小临界载荷:2EIminFcr2l——两端铰支细长压杆的临界载荷的欧拉公式23 2EImin欧拉临界力公式Fcr2中的Imin如何确定？(l)定性确定Imin24 二、支承对压杆临界载荷的影响临界载荷欧拉公式的一般形式:两端铰支:＝1.02EI一端自由，一端固定:＝2.0F一端铰支，一端固定:＝0.7cr2(l)两端固定:＝0.5两端固支但一端可横移:＝1.025 临界载荷欧拉公式的一般形式:2一端自由，一端固定:＝2.0EIF一端铰支，一端固定:＝0.7cr2两端固定:＝0.5(l)两端铰支:＝1.0注意当压杆杆端的约束情况在最大和最小抗弯刚度平面内完全相同时，则上式中的I应取压杆横截面的最小形心主惯性矩I。min2EIminFcr2(l)如果压杆在最大和最小抗弯刚度平面内的约束情况不相同时，则应分别计算在两个形心主惯性平面内失稳时的临界力，然后再确定该压杆的临界力。26 2EI临界载荷欧拉公式的一般形式:Fcr2(l)如果压杆在最大和最小抗弯刚度平面内的约束情况不相同时，则应分别计算在两个形心主惯性平面内失稳时的临界力，然后再确定该压杆的临界力。2EIzFcrz2(L)zz2EIyFcry2(L)yyFmin(F,F)crcrycrz27 例：一根30×5mm2矩形截面木杆，对其施加轴向压力，若材料的抗压强度c40MPa，当长度分别l130mm,l21000mm时，求临界压力:Pcr.木材:(E10GPa).Pcr木杆两端约束可视为铰支PP解：1、短杆是强度问题PA30540l16kN1cP2、细长杆是稳定问题l2hb33305II312.5mm4minyy12122EIzminPP1cr2lPPcr229121010312.5102130.84(N)P1/P2200.28 例：图示细长圆截面连杆，长度l800mm，直径d20mm,材料为Q235钢，E＝200GPa.试计算连杆的临界载荷F.crB解：1、细长压杆的临界载荷FcrA224EIEdFlcr2264yll394200100.02z20.86424.2(kN)2、从强度分析s235MPa20.02673.8(kN)FA23510crs429 例：求下列细长压杆的临界力。（L=0.5m，E=200GPa）PP解：图（a）一端固定，一端铰支3501040.7,Imin4167mm122EI23min416720010Fcr22(l)(0.7500)LLFcr67.14kN图（b）一端固定，一端铰支442,Iy14.76cm,Iz3.89cm.查表，II3.89108m4图（a）图（b）minzzy2EI286min0.389102001010Fcr22(l)(20.5)50Fcr76.8kN30 例：求下列细长压杆的临界力。(在xz平面内失稳，为两端铰支，长L；在xy平面内失稳，为一端固定，一端铰支，长L）21解：①、xz平面内绕y轴失稳，两端铰支：2b3hEIyy=1，Iy,Fcry212L2②、xy平面内绕z轴失稳，左端固定，右端铰支：32bhEI=0.7，I,Fzzzcrz212(0.7L)1③、压杆的临界力Fmin(F,F)31crcrycrz 例：求下列细长压杆的临界力。（L=0.5m，E=200GPa）2(45284)解：一端固定，一端自由P2,44查表：Iz5.69cm,Iy3.0cm.(a)4图Izc25.6911.38cmzc4Iyc23.06.0cmyc(a)4LIminIyc6.0cm2243EI61020010minFcr22z(l)(2.0500)yFcr118.4kN(b)32 §11-3欧拉公式的使用范围临界应力总图一、临界应力与柔度2222FcrEIE2EEcr22il2A(l)A(l)()2i——临界应力的欧拉公式l——压杆的柔度（长细比）i综合反映杆长、支持方柔度是影响压杆承载能力的综合指标。式与截面几何性质对临界应力的影响I2i——惯性半径IzAiz,A2IyAiy.压杆容易失稳cr33 二、欧拉公式的适用范围2Ep,crpcr2p.22EE（细长压杆临界柔度）ppp欧拉公式的适用范围:p，称大柔度杆（细长压杆）例：Q235钢，E200GPa,p200MPa.223E20010p99.35100p200当≤p时，通过不同试样的试验测得临界压力，再回归处理。34 1、大柔度杆（细长压杆）采用欧拉公式计算。22EIEp(p)临界压力：Fcr2临界压应力：cr2(l)2：中柔度杆（中长压杆）采用经验公式计算。sp(ps)ascrab——直线型经验公式sba,b是与材料性材料a(MPa)b(MPa)ps能有关的常数。Q2353041.1210062见P293表11-2。硅钢5783.74410060直线公式适合合铬钼钢9805.296550金钢、铝合金、铸硬铝3722.15500铁与松木等中柔度压杆。铸铁331.91.45435松木28.70.1959 3：小柔度杆（短粗压杆）只需进行强度计算。FN()crsssA三、临界应力总图：临界应力与柔度之间的变化关系图。crab——直线型经验公式crS2PE细长压杆。cr2粗短杆中柔度杆大柔度杆loi36sP 粗短杆中长杆细长杆细长杆—发生弹性屈曲(p)中长杆—发生弹塑性屈曲(s<p)粗短杆—不发生屈曲，而发生屈服(<s)37 中柔度杆——抛物线型经验公式2[1a()]crsca,是与材料性能有关的常数。c抛物线公式适合于结构钢与低合金钢等制做的中柔度压杆。对于Q215、Q235钢及16Mn钢，取a=0.43。Ecr2这样，[1a()]ccrs0.57sc0.57C2Escr2λOλC38 对于Q235钢，s=235MPa,E=200GPa，有：22350.00668,123crc对于16Mn钢，s=343MPa,E=200GPa，有：23430.0146,100.5crc不同材料，具有不同的材料常数。四、注意问题：1、计算临界力、临界应力时，先计算柔度，判断所用公式。2、对局部面积有削弱的压杆，计算临界力、临界应力时，其截面面积和惯性距按未削弱的尺寸计算。但进行强度计算时需按削弱后的尺寸计算。39 例两端铰支压杆的长度l=1.2m，材料为Q钢，E=200GPa，235200MPa，240MPa。已知截面的面积A=900mm2，若截面的Ps形状分别为圆形、正方形、d/D=0.7的空心圆管。试分别计算各杆的临界力。ID解（1）圆形截面iA4直径D4A490033.85mm33.85103m43ID/64D33.85103惯性半径i8.4610m2AD/4449l11.2E20010柔度3142P699.3i8.4610P20010因为14299.3，所以属细长压杆，用欧拉公式计算临界力P293422001033.8510EI64F88.3kNcr2240l11.2 例两端铰支压杆的长度l=1.2m，材料为Q钢，E=200GPa，235200MPa，240MPa。已知截面的面积A=900mm2，若截面的Ps形状分别为圆形、正方形、d/D=0.7的空心圆管。试分别计算各杆的临界力。Ia（2）正方形截面iA12截面边长aA3m900301043Ia/12a30103惯性半径i8.6610m2Aa1212l11.2柔度1383i8.6610因为13899.3，所以属细长压杆，用欧拉公式计算临界力。P291342200103010EI12F92.5kNcr22l11.241 例两端铰支压杆的长度l=1.2m，材料为Q钢，E=200GPa，235200MPa，240MPa。已知截面的面积A=900mm2，若截面的Ps形状分别为圆形、正方形、d/D=0.7的空心圆管。试分别计算各杆的临界力。22IDd（3）空心圆管截面iA422222因为d/D=0.7，所以DdD0.7DA900mm44解得：D=47.4×10-3m，d=33.18×10-3m44441274惯性矩IDd47.433.18101.8810m64644422I(Dd)/64Ddi22A(Dd)/44惯性半径71.881021.4510m690010柔度l11.282.712i1.4510as3042404257.10b1.12 例两端铰支压杆的长度l=1.2m，材料为Q钢，E=200GPa，235200MPa，240MPa。已知截面的面积A=900mm2，若截面的Ps形状分别为圆形、正方形、d/D=0.7的空心圆管。试分别计算各杆的临界力。l11.282.7（3）空心圆管截面12i1.4510Eas304240P99.3057.1b1.12P因为，所以属中长压杆，现采用直线公式（也可SP采用抛物线公式）计算临界力。FabAcr663041.1282.71090010190kN讨论三根杆件截面积均相同，但临界力相差很大，空心圆管截面具有最大的临界力。这说明此种截面较为合理，具有较大的惯性矩和惯性半径，从而使得柔度值比较小。43 例：一压杆长L=1.5m，由两根56566等边角钢组成，两端铰支，压力F=150kN，角钢为Q235钢，求临界压力（=304-1.12）。cr解：查表：一个角钢：244A8.367cm,I23.63cm,I47.24cm1y1z14两根角钢图示组合之后II92.48cmyz4II2I223.6347.26cmzminyy11I47.26mini1.68cmminy1A28.367l150maxl1189.2.3imin1.681282.7i1.4510a304235sQ235钢p100061.6b1.1244 例：一压杆长L=1.5m，由两根56566等边角钢组成，两端铰支，压力F=150kN，角钢为Q235钢，求临界压力（=304-1.12）。crl150max89.3i1.68minl11.2p1001282.7i1.4510Q235钢a304235s61.60b1.12<0p所以，应由经验公式求临界压力。σ=304-1.12=304-1.12×89.3=204（MPa）cr临界压力2FA28.36710204314.4(kN)crcr45 例．截面为120×200mm的矩形木柱，材料的弹性模量E=1×104Mpa,。其支承情况为：在xoz平面失稳（即绕y轴失稳）时柱的两端可视为固定端（图a）；在xoy平面失稳（即绕z轴失稳）时，柱的两端可视为铰支端（图b）。试求该木柱的临界力。解：(1)计算在xoz平面绕y轴失稳时的柔度两端固定：μ=0.5yIbyim0.0346;yA23yl0.57101yi0.0346y(2)计算在xoy平面绕z轴失稳时的柔度两端铰支：μ=1.0zIhzim0.0577;zA23zl17121ziz0.057746 例．截面为120×200mm的矩形木柱，材料的弹性模量E=1×104Mpa,。其支承情况为：在xoz平面失稳（即绕y轴失稳）时柱的两端可视为固定端（图a）；在xoy平面失稳（即绕z轴失稳）时，柱的两端可视为铰支端Ibyim0.0346;（图by）。试求该木柱的临界力。A23Iyl0.57hz101imyi0.03460.0577;zAy23zl17121zi0.0577z从上面计算可知：>（必先绕z轴失稳）zy(3)计算临界力121,maxz46E1010110p6p810>，为细长压杆可由欧拉公式计算临界力maxp47 例．截面为120×200mm的矩形木柱，材料的弹性模量E=1×104Mpa,。其支承情况为：在xoz平面失稳（即绕y轴失稳）时柱的两端可视为固定端（图a）；在xoy平面失稳（即绕z轴失稳）时，柱的两端可视为铰支端（图b）。试求该木柱的临界力。(3)计算临界力从上面计算可知：λ>λ（必先绕z轴失稳）zy121,maxz46E1010110p6p810>，为细长压杆，可由欧拉公式计算临界力maxp22EIEAzP　或　　PA161KNcr22crcrzlz该柱将可能在xoy平面内失稳（绕z轴）。48