福建省厦门市高三数学上学期期末质量检查试题 文

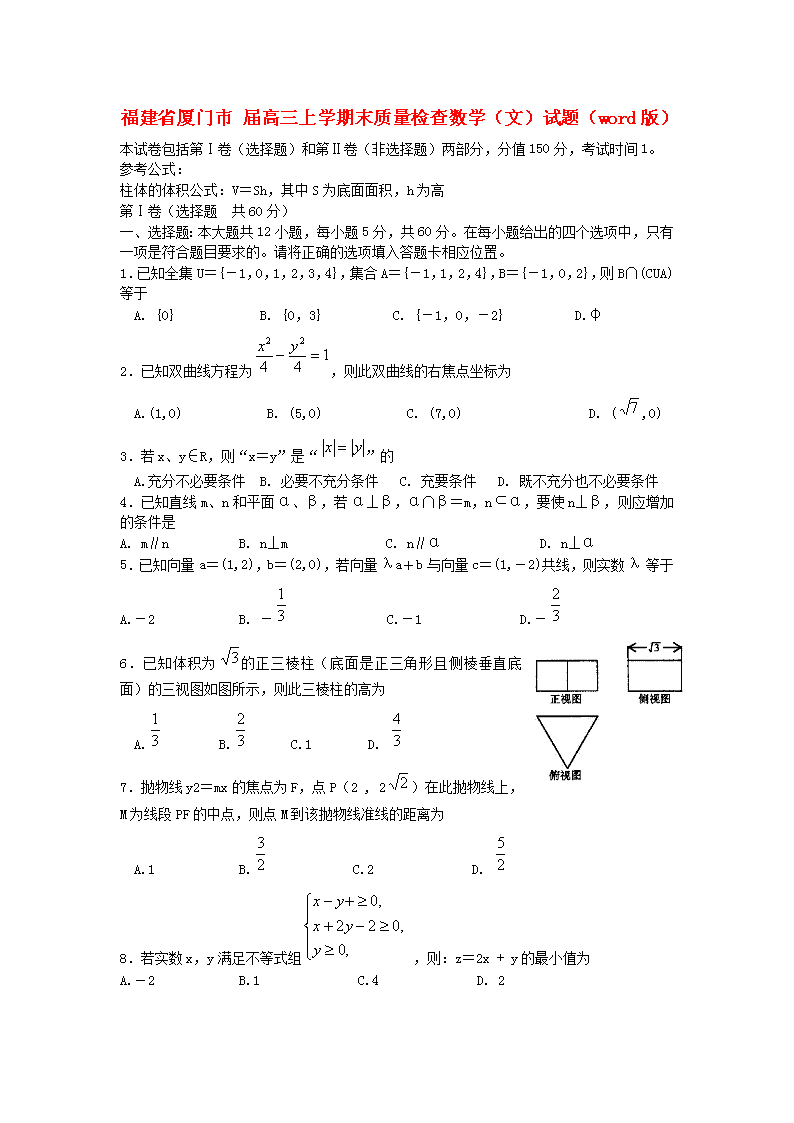
'福建省厦门市届高三上学期末质量检查数学（文）试题（word版）本试卷包括第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，分值150分，考试时间1。参考公式：柱体的体积公式：V＝Sh，其中S为底面面积，h为高第Ⅰ卷（选择题　共60分）一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。请将正确的选项填入答题卡相应位置。1．已知全集U＝{－1，0，1，2，3，4}，集合A＝{－1，1，2，4}，B＝{－1，0，2}，则B∩(CUA)等于　A.{0}　　　　　　B.{0，3}　　　　　C.{－1，0，－2}　　　　　D.φ2．已知双曲线方程为，则此双曲线的右焦点坐标为　A.(1,0)　　　　　　B.(5,0)　　　　　　C.(7,0)　　　　　　　　　D.(,0)3．若x、y∈R，则“x＝y”是“”的　A.充分不必要条件　B.必要不充分条件C.充要条件D.既不充分也不必要条件4．已知直线m、n和平面α、β，若α⊥β，α∩β＝m，nα，要使n⊥β，则应增加的条件是A.m∥n　　　　　B.n⊥m　　　　　　　C.n∥α　　　　　　　D.n⊥α5．已知向量a＝(1,2)，b＝(2,0)，若向量λa＋b与向量c＝(1,－2)共线，则实数λ等于A.－2　　　　　　B.－　　　　　　　C.－1　　　　　　　D.－6．已知体积为的正三棱柱（底面是正三角形且侧棱垂直底面）的三视图如图所示，则此三棱柱的高为　A.　　　　B.　　　C.1　　　　D.7．抛物线y2＝mx的焦点为F，点P（2,2）在此抛物线上，M为线段PF的中点，则点M到该抛物线准线的距离为　A.1　　　　　　B.　　　　　　C.2　　　　　　　D.8．若实数x，y满足不等式组，则：z＝2x+y的最小值为A.－2　　　　　　B.1　　　　　　　C.4　　　　　　　D.2 9．如图，已知，，·，∠AOP＝，若，则实数t等于A.　　　　B.　　　C.　　　　D.310．对任意x、y∈R，恒有sinx＋cosy＝2sin()cos()，则sin等于A.　　　　　B.　　　　C.　　　　　D.11．函数y＝(3－x2)ex的单调递增区是　A.(－∞,0)　　　　　B.(0,＋∞)　　　　C.(－∞,－3)和(1,＋∞)　　　　　D.(－3,1)　12．已知函数f(x)＝Asin()(A>0，0<<)的部分图象如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为(2，A)，点R的坐标为(2，0)。若∠PRQ＝，则y＝f(x)的最大值及的值分别是A.2,　　　　　B.,　　C.,　　　　　D.2,　第Ⅱ卷（非选择题　共90分）二、填空题：本大题共4小题，每小题4分，共16分，把答案填写在答题卡的相应位置。13．已知数列为等差数列，且a1＋a6＋a11＝3，则a3＋a9＝　　▲　　。14．函数f(x)＝sin(x＋)－cos(x＋)，x∈[0,2π]的单调递减区间是　　▲　　。 15．已知函数f(x)＝　，则不等式f(x)＞f(1)的解集是　　▲　　。16．设函数f(x)＝对任意x1、x2∈(0,＋∞)，不等式恒成立，则正数k的取值范围是　　▲　　。三、解答题：本大题共6小题，共74分。解答应写出文字说明、证明过程或演算步骤。把解答过程写在答题卡的相应位置。17．（本小题满分12分）　　在△ABC中，a、b、c分别是三个内角A、B、C的对边，a＝2，sin且△ABC的面积为4　　（Ⅰ）求cosB的值；　　（Ⅱ）求边b、c的长。18．（本小题满分12分）　　如图，在四棱锥P－ABCD中，PD⊥平面ABCD，AB＝BC，BD⊥AC，E为PC的中点。　　（Ⅰ）求证：AC⊥PB；　　（Ⅱ）求证：PA∥平面BDE。19．（本小题满分12分）　　已知偶函数f(x)＝x2＋bx＋c(常数b、c∈R)的一个零点为1，直线l：y＝kx+m(k＞m∈R)与函数y＝f(x)的图象相比。　　（Ⅰ）求函数y＝f(x)的解析式；　　（Ⅱ）求的取值范围。 本小题满分12分）　　已知椭圆E：=1(a＞b＞o)的离心率e=，且经过点(,1)，O为坐标原点。（Ⅰ）求椭圆E的标准方程；　　（Ⅱ）圆O是以椭圆E的长轴为直径的圆，M是直线x=－4在x轴上方的一点，过M作圆O的两条切线，切点分别为P、Q，当∠PMQ=60°时，求直线PQ的方程。21．（本小题满分12分）某软件公司新开发一款学习软件，该软件把学科知识设计为由易到难共12关的闯关游戏．为了激发闯关热情，每闯过一关都奖励若干慧币（一种网络虚拟币）．该软件提供了三种奖励方案：第一种，每闯过一关奖励40慧币；第二种，闯过第一关奖励4慧币，以后每一关比前一关多奖励4慧币；第三种，闯过第一关奖励0.5慧币，以后每一关比前一关奖励翻一番（即增加1倍），游戏规定：闯关者须于闯关前任选一种奖励方案．（Ⅰ）设闯过n(n∈N，且n≤12）关后三种奖励方案获得的慧币依次为An，Bn，Cn，试求出An，Bn，Cn的表达式；（Ⅱ）如果你是一名闯关者，为了得到更多的慧币，你应如何选择奖励方案？22．（本小题满分14分）设函数f(x)=－x3＋mx2+x，g(x)=mx2－x＋c，F(x)=xf(x)。(Ⅰ)若函数y=f(x)在x=2处有极值，求实数m的值；(Ⅱ)试讨论方程y=F＇(x)＝g(x)的实数解的个数； （Ⅲ）记函数y=G(x)的导称函数G＇(　x)在区间(a,b)上的导函数为G＇＇(　x)，若在(a，b)上G＇＇(　x)＞0恒成立，则称函数G(x)(a,b)上为“凹函数”。若存在实数m∈[－2,2],使得函数F(x)在(a,b)上为“凹函数”，求b－a最大值。 '