湖北省荆州市2013届高三3月第二次质量检查数学（文）试题 word版含答案

'湖北省荆州市2013届高中毕业班质量检查(II)数学（文）试题本试卷共三大题２２道小题，满分１５０分，考试用时１２０分钟。注意事项：１答卷前，考生务必将自己的学校、班级、姓名、考号填在试卷答题卡上。２第１至１０小题选出答案后，用２Ｂ铅笔把答题卡上对应的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号。第１１至２２题用０．５毫米黑色签字笔在答题卡上作答，答在试题卷上的无效。３．考试结束，只交答题卡。本科目考试时间：２０１３年３月１２日下午１５∶００———１７∶００一、选择题：本大题共１０小题，每小题５分，共５０分．在每小题给出的四个选项中，只有一项正确，每小题选出答案后，用２Ｂ铅笔把答题卡上对应题目的答案标号涂黑，多涂、不涂或涂错均得０分．１．已知复数ｚ满足ｚｉ＝１＋ｉ，则ｚ＝Ａ．１＋ｉ　　　　　Ｂ．ｉ　　　　　Ｃ．－ｉ　　　　　Ｄ．１－ｉ２．某班有５４名同学，准备派６名同学参加某高校组织的夏令营活动。现将５４名同学编号（１～５４），用系统抽样的方法抽取，已知５号在样本中，则样本中最大的号码是Ａ．５０　　　　　Ｂ．５１　　　　　Ｃ．５２　　　　　Ｄ．５３３．已知集合Ａ＝｛ｘ│≥０｝，集合Ｂ＝｛ｙ│ｙ＝ｓｉｎｘ，ｘ∈Ｒ｝，则Ｂ∩ＣＲＡ＝Ａ．Φ　　　　　Ｂ．｛－１｝　　　　　Ｃ．｛１｝　　　　　Ｄ．｛－１，１｝４．已知变量ｘ，ｙ满足约束条件，则目标函数ｚ＝３ｘ＋ｙ的最小值为Ａ．１２　　　　　　Ｂ．１１　　　　　　Ｃ．８　　　　　　Ｄ．－１５．设l，ｍ，ｎ为不重合的三条直线，其中直线ｍ，ｎ在平面α内，则“ｌ⊥α”是“l⊥ｍ且l⊥ｎ”的Ａ．充要条件　　　　　　　　　　　　　Ｂ．充分不必要条件Ｃ．必要不充分条件Ｄ．既不充分也不必要条件６．某程序的流程图如图所示，若使输出的结果不大于３８，则输入的整数ｉ的最大值为 Ａ．４　　　　　Ｂ．５　　　　　Ｃ．６　　　　　Ｄ．７７．在△ＡＢＣ中，Ｏ是中线ＡＭ上一个动点，若ＡＭ＝４，则的最小值是Ａ．－４　　　　Ｂ．－８　　　　Ｃ．－１０　　　　Ｄ．－１２８．设一个四面体的体积为Ｖ１，且它的各条棱的中点构成一个凸多面体，其体积为Ｖ２，则Ｖ２/Ｖ１为Ａ．１/２　　　　　Ｂ．２/３　　　　　Ｃ．３/４　　　　　Ｄ．５/６９．以下四个命题（１）在△ＡＢＣ中，内角Ａ，Ｂ，Ｃ的对边分别为ａ，ｂ，ｃ，且ｂｓｉｎＡ＝ａｃｏｓＢ，则Ｂ＝π/４；（２）设ａ，ｂ是两个非零向量且│ａ·ｂ│＝│ａ│·│ｂ│，则存在实数λ，使得ｂ＝λａ；（３）函数ｆ（ｘ）＝ｓｉｎ－ｘ在Ｒ上的零点有且仅有一个；（４）ａ，ｂ∈Ｒ且，则ａ＞ｂ．其中正确的个数有Ａ．１个　　　　　Ｂ．２个　　　　　Ｃ．３个　　　　　Ｄ．４个１０．已知函数ｆ（ｘ）在Ｒ上可导，下列四个选项中正确的是Ａ．若ｆ（ｘ）＞ｆ＇（ｘ）对ｘ∈Ｒ恒成立，则ｅｆ（１）＜ｆ（２）Ｂ．若ｆ（ｘ）＜ｆ＇（ｘ）对ｘ∈Ｒ恒成立，则ｆ（－１）＞ｆ（１）Ｃ．若ｆ（ｘ）＋ｆ＇（ｘ）＞０对ｘ∈Ｒ恒成立，则ｅｆ（２）＜ｆ（１）Ｄ．若ｆ（ｘ）＋ｆ＇（ｘ）＜０对ｘ∈Ｒ恒成立，则ｆ（－１）＞ｆ（１）二、填空题：本大题共７小题，每小题５分，共３５分，把答案填在答题卡中相应的横线上．１１．若函数ｆ（ｘ）＝为奇函数，则实数ｍ＝　　　　　． 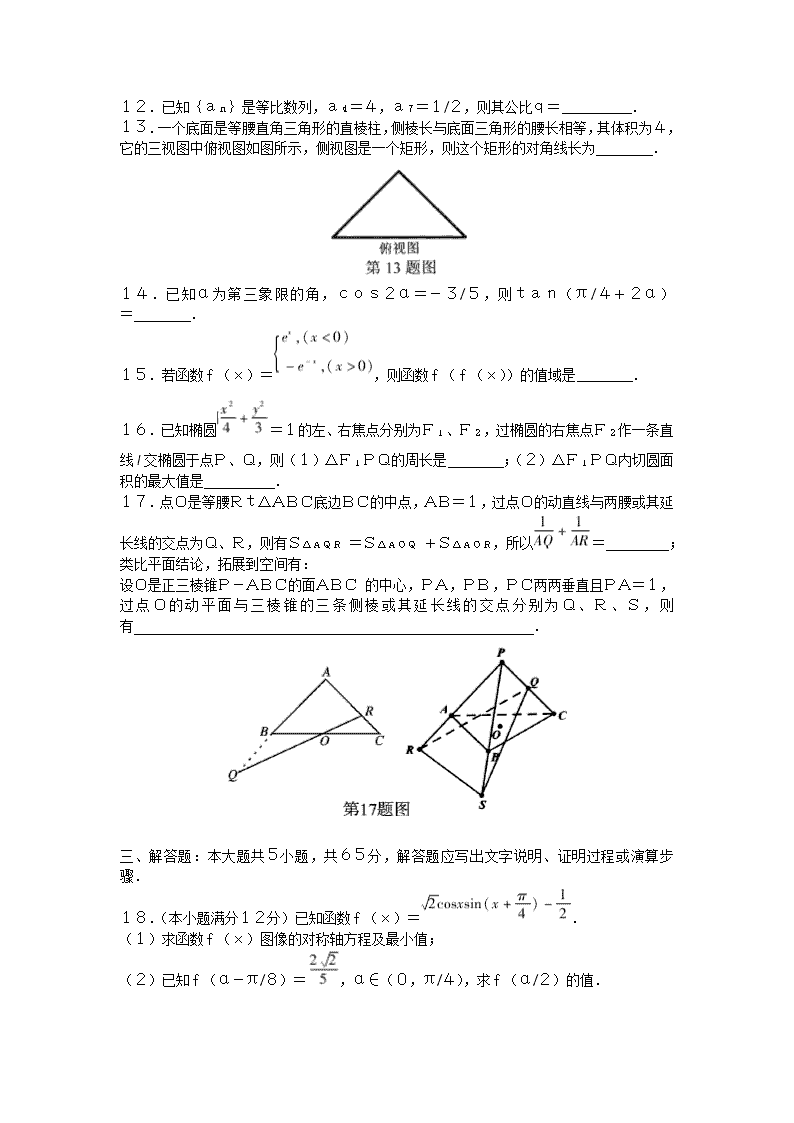１２．已知｛ａｎ｝是等比数列，ａ４＝４，ａ７＝１/２，则其公比ｑ＝　　　　　．１３．一个底面是等腰直角三角形的直棱柱，侧棱长与底面三角形的腰长相等，其体积为４，它的三视图中俯视图如图所示，侧视图是一个矩形，则这个矩形的对角线长为　　　　．１４．已知α为第三象限的角，ｃｏｓ２α＝－３/５，则ｔａｎ（π/４＋２α）＝　　　　．１５．若函数ｆ（ｘ）＝，则函数ｆ（ｆ（ｘ））的值域是　　　　．１６．已知椭圆＝１的左、右焦点分别为Ｆ１、Ｆ２，过椭圆的右焦点Ｆ２作一条直线l交椭圆于点Ｐ、Ｑ，则（１）△Ｆ１ＰＱ的周长是　　　　；（２）△Ｆ１ＰＱ内切圆面积的最大值是　．１７．点Ｏ是等腰Ｒｔ△ＡＢＣ底边ＢＣ的中点，ＡＢ＝１，过点Ｏ的动直线与两腰或其延长线的交点为Ｑ、Ｒ，则有Ｓ△ＡＱＲ＝Ｓ△ＡＯＱ＋Ｓ△ＡＯＲ，所以＝　　；类比平面结论，拓展到空间有：设Ｏ是正三棱锥Ｐ－ＡＢＣ的面ＡＢＣ的中心，ＰＡ，ＰＢ，ＰＣ两两垂直且ＰＡ＝１，过点Ｏ的动平面与三棱锥的三条侧棱或其延长线的交点分别为Ｑ、Ｒ、Ｓ，则有　．三、解答题：本大题共５小题，共６５分，解答题应写出文字说明、证明过程或演算步骤．１８．（本小题满分１２分）已知函数ｆ（ｘ）＝．（１）求函数ｆ（ｘ）图像的对称轴方程及最小值；（２）已知ｆ（α－π/８）＝，α∈（０，π/４），求ｆ（α/２）的值． １９．（本小题满分１２分）在等差数列｛｝中，＝３，其前ｎ项和为Ｓｎ；在各项均为正数的等比数列｛ｂｎ｝中，ｂ１＝１，且ｂ２＋Ｓ２＝１２，Ｓ５＝５ｂ３．（１）求｛｝与｛ｂｎ｝的通项公式；（２）设数列｛ｃｎ｝满足ｃｎ＝，求数列｛ｃｎ｝前ｎ项和Ｔｎ，并证明Ｔｎ＜０（ｎ∈）．２０．（本小题满分１３分）２０１３年６月６日是第１８个全国“爱眼日”．某校为了解学生近视情况，决定按１０％的比例对高一、高二近视在１００度以上的７００名学生按年级进行抽样检查，测得近视度的频数分布表如下表１、表２．表１：高二年级学生近视度频数分布表表２：高一年级学生近视度频数分布表（１）求该校高二年级近视在１００度以上的人数并完成下面频率分布直方图；（２）估计高一年级学生近视度的平均值； （３）从样本中近视度在［５００，７００）之间的学生中任选２人，求至少有１人近视度在［６００，７００）之间的概率．２１．（本小题满分１４分）已知圆Ｃ：＝８及点Ｆ（１，０），Ｐ为圆Ｃ上一动点，在同一坐标平面内的动点Ｍ满足：,││＝││．（１）求动点Ｍ的轨迹Ｅ的方程；（２）过点Ｆ作直线l与（１）中轨迹Ｅ交于不同两点Ｒ，Ｓ，设＝λ，λ∈［－２，－１），求直线l的纵截距的取值范围．２２．（本小题满分１４分）已知ｆ（ｘ）＝．（１）当ａ＞０时，求函数ｆ（ｘ）的最小值；（２）当ａ＝１时，是否存在过点（１，－１）的直线与函数ｙ＝ｆ（ｘ）的图像相切？若存在，有多少条？若不存在，说明理由；（３）求证：对任意正整数ｎ均有. www.ks5u.comwww.ks5u.comwww.ks5u.com'