材料力学课件第六章.ppt

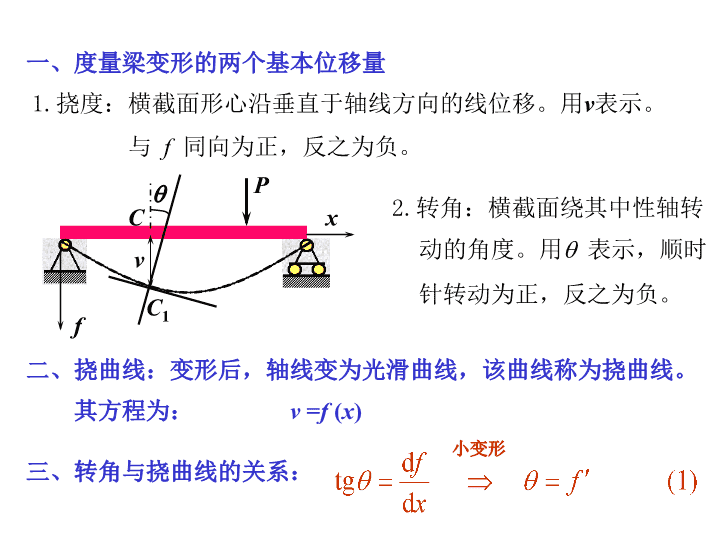
第六章弯曲变形工程中的弯曲变形问题挠曲线的微分方程及用积分法求弯曲变形用叠加法求弯曲变形梁的刚度校核弯曲超静定 研究范围：等直梁在对称弯曲时位移的计算。研究目的：①对梁作刚度校核；②解超静定梁（变形几何条件提供补充方程）。第一节工程中的弯曲变形问题 1.挠度：横截面形心沿垂直于轴线方向的线位移。用v表示。与f同向为正，反之为负。2.转角：横截面绕其中性轴转动的角度。用表示，顺时针转动为正，反之为负。二、挠曲线：变形后，轴线变为光滑曲线，该曲线称为挠曲线。其方程为：v=f(x)三、转角与挠曲线的关系：一、度量梁变形的两个基本位移量小变形PxvCqC1f 一、挠曲线近似微分方程式（2）就是挠曲线近似微分方程。小变形fxM>0fxM<0第二节挠曲线的微分方程及用积分法求弯曲变形 对于等截面直梁，挠曲线近似微分方程可写成如下形式：二、求挠曲线方程（弹性曲线）1.微分方程的积分2.位移边界条件PABCPD 讨论：①适用于小变形情况下、线弹性材料、细长构件的平面弯曲。②可应用于求解承受各种载荷的等截面或变截面梁的位移。③积分常数由挠曲线变形的几何相容条件（边界条件、连续条件）确定。④优点：使用范围广，直接求出较精确；缺点：计算较繁。支点位移条件：连续条件：光滑条件： 例1求下列各等截面直梁的弹性曲线、最大挠度及最大转角。建立坐标系并写出弯矩方程写出微分方程的积分并积分应用位移边界条件求积分常数解：PLxf 写出弹性曲线方程并画出曲线最大挠度及最大转角xfPL 解：建立坐标系并写出弯矩方程写出微分方程的积分并积分xfPLa 应用位移边界条件求积分常数PLaxf 写出弹性曲线方程并画出曲线最大挠度及最大转角PLaxf 一、载荷叠加：多个载荷同时作用于结构而引起的变形等于每个载荷单独作用于结构而引起的变形的代数和。二、结构形式叠加（逐段刚化法）：第三节用叠加法求弯曲变形 例4按叠加原理求A点转角和C点挠度。解、载荷分解如图由梁的简单载荷变形表，查简单载荷引起的变形。qqPP=+AAABBBCaa qqPP=+AAABBBCaa叠加 例6结构形式叠加（逐段刚化法)原理说明。=+PL1L2ABCBCPL2f1f2等价等价xfxffPL1L2ABC刚化AC段PL1L2ABC刚化BC段PL1L2ABCMxf 其中[]称为许用转角；[f/L]称为许用挠跨比。通常依此条件进行如下三种刚度计算：、校核刚度：、设计截面尺寸；、设计载荷。(但：对于土建工程，强度常处于主要地位，刚度常处于从属地位。特殊构件例外）第四节梁的刚度校核 PL=400mmP2=2kNACa=0.1m200mmDP1=1kNB例7下图为一空心圆杆，内外径分别为：d=40mm、D=80mm，杆的E=210GPa，工程规定C点的[f/L]=0.00001,B点的[]=0.001弧度,试核此杆的刚度。=++=P1=1kNABDCP2BCDAP2=2kNBCDAP2BCaP2BCDAM P2BCa=++图1图2图3PL=400mmP2=2kNACa=0.1m200mmDP1=1kNBP1=1kNABDCP2BCDAMxf叠加求复杂载荷下的变形 校核刚度 1、处理方法：变形协调方程、物理方程与平衡方程相结合，求全部未知力。解：建立静定基确定超静定次数，用反力代替多余约束所得到的结构——静定基。=q0LABLq0MABAq0LRBABxf第五节弯曲超静定 几何方程——变形协调方程+q0LRBAB=RBABq0AB物理方程——变形与力的关系补充方程求解其它问题（反力、应力、变形等） 几何方程——变形协调方程：解：建立静定基=例10结构如图，求B点反力。LBCxfq0LRBABCq0LRBAB=RBAB+q0AB =LBCxfq0LRBABCRBAB+q0AB物理方程——变形与力的关系补充方程求解其它问题（反力、应力、变形等） 强度：正应力：剪应力：刚度：稳定性：都与内力和截面性质有关。第六节提高弯曲刚度的措施 一、选择梁的合理截面矩形木梁的合理高宽比北宋李诫于1100年著«营造法式»一书中指出:矩形木梁的合理高宽比(h/b=)1.5英(T.Young)于1807年著«自然哲学与机械技术讲义»一书中指出:矩形木梁的合理高宽比为Rbh 一般的合理截面1、在面积相等的情况下，选择抗弯模量大的截面zDzaa zD0.8Da12a1z 工字形截面与框形截面类似。0.8a2a21.6a22a2z 2、根据材料特性选择截面形状sGz如铸铁类材料，常用T字形类的截面，如下图：二、采用变截面梁最好是等强度梁，即若为等强度矩形截面，则高为同时Px 三、合理布置外力（包括支座），使Mmax尽可能小。PL/2L/2Mx+PL/4PL/43L/4Mx3PL/16P=qLL/54L/5对称MxqL2/10 MxqLL/5qL/5402qL502qL-MxqL/2L/2322qL-Mx