材料力学课件 第六章弯曲应力1.ppt

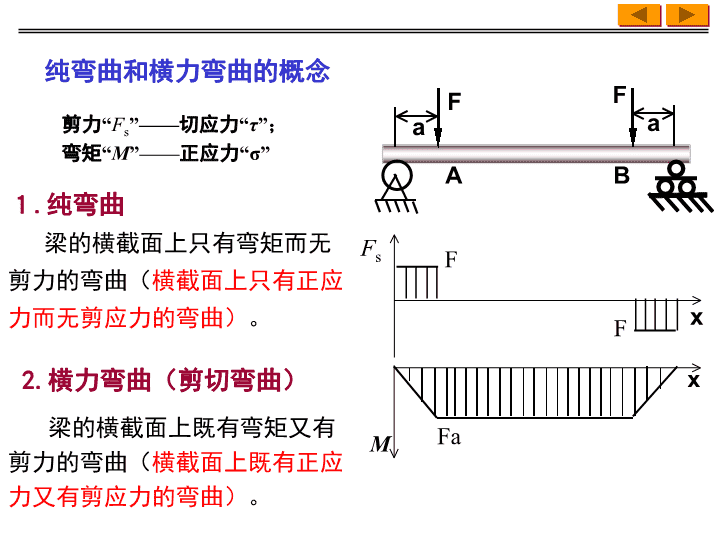
§6-1梁弯曲时的应力及强度计算 １.纯弯曲梁的横截面上只有弯矩而无剪力的弯曲（横截面上只有正应力而无剪应力的弯曲）。剪力“Fs”——切应力“τ”；弯矩“M”——正应力“σ”2.横力弯曲（剪切弯曲）aaFBAFMxFsxFaFF梁的横截面上既有弯矩又有剪力的弯曲（横截面上既有正应力又有剪应力的弯曲）。纯弯曲和横力弯曲的概念 （一）变形几何关系：由纯弯曲的变形规律→纵向线应变的变化规律。1、观察实验：一、纯弯曲梁横截面上的正应力公式 abcdabcdMM2、变形规律：⑴、横向线：仍为直线，只是相对转动了一个角度且仍与纵向线正交。⑵、纵向线：由直线变为曲线，且靠近上部的纤维缩短，靠近下部的纤维伸长。3、假设：（1）弯曲平面假设：梁变形前原为平面的横截面变形后仍为平面，且仍垂直于变形后的轴线，只是各横截面绕其上的某轴转动了一个角度。 凹入一侧纤维缩短突出一侧纤维伸长根据变形的连续性可知，梁弯曲时从其凹入一侧的纵向线缩短区到其凸出一侧的纵向线伸长区，中间必有一层纵向无长度改变的过渡层--------称为中性层。中间层与横截面的交线－－中性轴（2）纵向纤维假设：梁是由许多纵向纤维组成的，且各纵向纤维之间无挤压。梁的弯曲变形实际上是各截面绕各自的中性轴转动了一个角度，等高度的一层纤维的变形完全相同。 yoo1AＢＢAabcdＢ１A１4、线应变的变化规律：dxyoo1在弹性范围内，（二）物理关系：由纵向线应变的变化规律→正应力的分布规律。abcd中性轴 应力的分布图：MZyσmaxσmax中性轴的位置？问题： yxMz（中性轴z轴为形心轴）（y轴为对称轴，自然满足）yzAσ——弯曲变形计算的基本公式（三）、静力方面：由横截面上的弯矩和正应力的关系→正应力的计算公式。中性轴 弯曲正应力计算公式。弯矩可代入绝对值，应力的符号由变形来判断。当M>0时，下拉上压；当M<0时，上拉下压。梁的抗弯刚度。ÞzEIyxMZyzAσ将上式代入式得：——弯曲变形计算的基本公式 中性轴z为横截面的对称轴时称为截面的抗弯截面系数yzzybh 中性轴z不是横截面的对称轴时Ozyytmaxycmax 几种简单截面的抗弯截面系数⑴矩形截面⑵圆形截面zybhyzd ⑶空心圆截面(4)型钢截面：参见型钢表式中DOdyz 二、纯弯曲理论的推广横力弯曲时：1、由于切应力的存在梁的横截面发生翘曲；2、横向力还使各纵向线之间发生挤压。平面假设和纵向线之间无挤压的假设实际上都不再成立。1m2mBA还能用吗？ 弹性力学的分析结果表明：对于细长梁（l/h>5），纯弯曲时的正应力计算公式用于横力弯曲情况，其结果仍足够精确。Fl4lF弯曲正应力公式可推广应用于横力弯曲和小曲率梁 例：厚为t=1.5mm的钢带，卷成直径D＝3m圆环。　　　　　。求：横截面上最大应力解：1）研究对象：单位宽条2）曲率公式：3）求应力： 例图示简支梁由56a号工字钢制成，已知F=150kN。试求危险截面上的最大正应力smax和同一横截面上翼缘与腹板交界处a点处的正应力sa。B5m10mAFCFAFB12.521166560za375kN.mM解：1、作弯矩图如上， 2、查型钢表得56号工字钢3、求正应力12.521166560zaB5m10mAFC375kN.mM a点处的正应力sa也可根据正应力沿梁高的线性分布规律来求12.521166560za 例：求图示悬臂梁的最大、压应力。已知：№10槽钢解：1）画弯矩图2）查型钢表：3）求应力：σcmaxσtmax