材料力学课件 应力状态分析.ppt

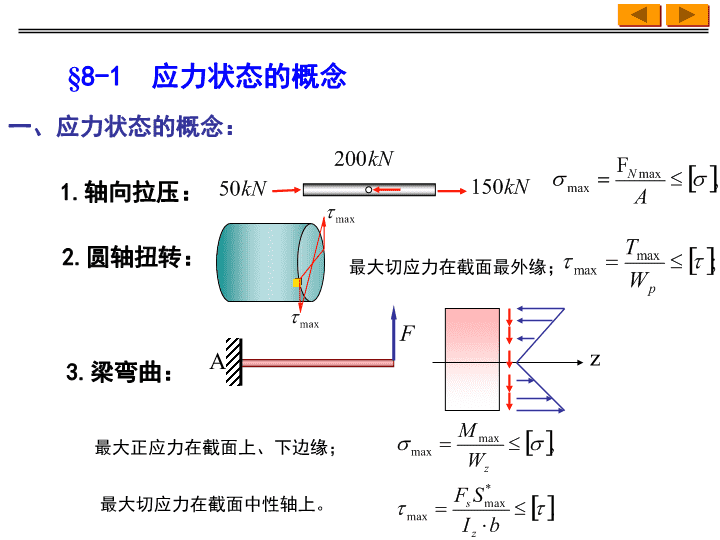
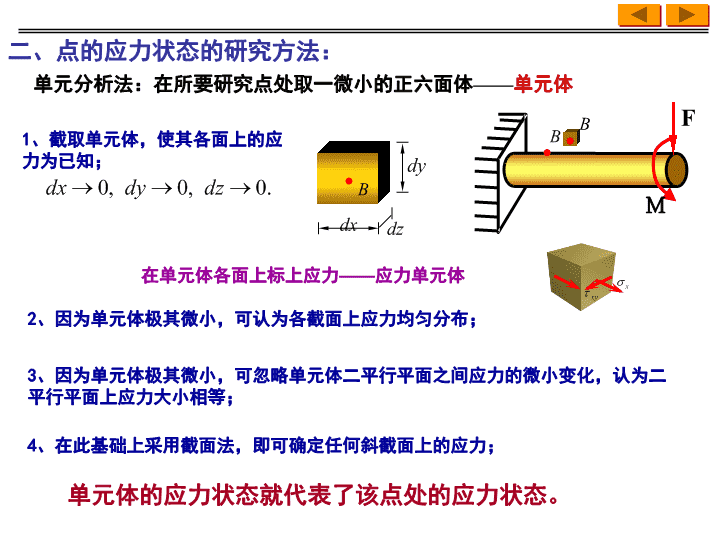
§8-1应力状态的概念§8-2平面应力状态分析——解析法§8-3平面应力状态分析——图解法（应力圆）§8-4空间应力的应力状态分析——一点的最大应力§8-5广义胡克定律§8-6强度理论概念第八章应力状态分析强度理论 一、应力状态的概念：3.梁弯曲：1.轴向拉压：2.圆轴扭转：最大切应力在截面最外缘；最大正应力在截面上、下边缘；最大切应力在截面中性轴上。zA§8-1应力状态的概念 1、截取单元体，使其各面上的应力为已知；2、因为单元体极其微小，可认为各截面上应力均匀分布；3、因为单元体极其微小，可忽略单元体二平行平面之间应力的微小变化，认为二平行平面上应力大小相等；4、在此基础上采用截面法，即可确定任何斜截面上的应力；单元体的应力状态就代表了该点处的应力状态。ＭF二、点的应力状态的研究方法：单元分析法：在所要研究点处取一微小的正六面体——单元体在单元体各面上标上应力——应力单元体B bcbcbbc横截面纵向水平面纵向铅垂面 取单元体示例FPl/2l/2S截面5432154321S截面 5432154321S截面1233t 取单元体示例FPlaS截面xzy4321S截面 yxzMzFsyT4321143忽略弯曲切应力 微体abcd （1）、主平面与主应力：主平面：切应力为零的平面。主应力：主平面上的正应力。主应力排列规定：按代数值由大到小。过一点总存在三对相互垂直的主平面，对应三个主应力301050单位：MPa3010三、主应力和主平面应力状态的分类 a、单向应力状态：只有一个主应力不等于零，另两个主应力都等于零的应力状态。b、二向应力状态：有两个主应力不等于零，另一个主应力等于零的应力状态。c、三向应力状态：三个主应力都不等于零的应力状态。（2)、应力状态的分类平面应力状态：单向应力状态和二向应力状态的总称。复杂应力状态：二向应力状态和三向应力状态的总称。空间应力状态：三向应力状态简单应力状态：单向应力状态。纯剪切应力状态：单元体上只存在剪应力无正应力。注：应力状态的分类，是根据主应力不等于零的个数来确定。 空间应力状态yxz平面应力状态xy xyxy单向应力状态纯剪应力状态 一、斜截面上的应力计算§8－2平面应力的应力状态分析—解析法等价空间问题简化为平面问题--逆时针转为正。 设：斜截面面积为ｄA，由分离体平衡得：单元体各面面积 由切应力互等定理和三角变换，可得：符号规定：1)“”正负号同“”；2)“ta”正负号同“t”；3)“a”为x轴正向与斜面的外法线间的夹角，逆时针为正，顺时针为负。注意：用公式计算时代入相应的正负号。——单元体任意斜截面上的应力计算式 主平面的方位——主应力的大小讨论：1)、2)、的极值主应力以及主平面方位可以确定出两个相互垂直的平面——主平面，分别为最大正应力和最小正应力所在平面。 3)、切应力ta的极值及所在截面——最大切应力所在的位置——xy面内的最大切应力由 ——主平面的位置——最大切应力所在的位置将与画在原单元体上。 例：如图所示单元体，求图示斜截面的应力及主应力、主平面。（单位：MPa）300405060解：1、求斜截面的应力 2、求主应力、主平面主应力：主平面位置： 例：如图所示单元体，求主应力及主平面。解：1、主应力2、主平面s1s33020单位：MPas1、s2、s3？ 空间应力状态：xy平面内的主应力： 这个方程恰好表示一个圆，这个圆称为应力圆§8-3平面应力的应力状态分析—图解法对上述方程消参数（2），得：一、应力圆：圆心：半径： RC应力圆：应力圆上任一点的横、纵坐标分别对应该点某一截面上正应力和切应力 二.应力圆的画法D(sx,txy)D’(sy,tyx)cRADxy 绘制步骤：1、取直角坐标系——2、取比例尺（严格按比例做图）。3、找点,.4、连交s轴于C点，以C为圆心，CD为半径画圆——应力圆。stoCDD’ 三、证明：证得圆心位置：证得半径为：stoCDD’ 四、图解法的应用以D为基点，转2a的圆心角至E点——，转向与单元体面转过的方向相同。2、主应力3、主平面位置以D为基点，转到A1点，其圆心角为2a0，逆时针时a0为“＋”；顺时针时a0为“－”。（a0——主平面的位置)。stoCD1、求斜截面上应力 4、切应力的极值及所在位置以D为基点，转到G1点，其圆心角为2a1。由应力圆可证明——最大正应力与最大剪应力所在平面相差450stoCD12a0 stoDD/B1B2A1A22α0E2αF证明：（2α角的关系）证毕 点面对应——应力圆上某一点的坐标值对应着单元体某一截面上的正应力和切应力几个对应关系D(sx,txy)D’(sy,tyx)cxyHnH转向对应——半径旋转方向与截面法线的旋转方向一致；二倍角对应——半径转过的角度是截面法线旋转角度的两倍。 D’60EFτσO2、量出所求的物理量解：1、按比例画此单元体对应的应力圆例：求1）图示单元体α=300斜截面上的应力2）主应力、主平面（单位：MPa）。 sxsxADtsodac2×45º2×45ºbeBE ttotsa(0,t)d(0,-t)ADbec2×45º2×45ºs1＝ts3＝tBEs3＝ts1＝tBE主应力单元体 Fqx12345yoxxy2x1梁的主应力及其主应力迹线xy3xxy4x5 Fqx12345yoxy3xxy2x1taosataosataosa1231313梁的主应力及其主应力迹线xxy413taosa4x5taosa5 主应力迹线（StressTrajectories)：主应力方向线的包洛线——曲线上每一点的切线都指示着该点的主拉应力方位（或主压应力方位）。实线表示主拉应力迹线；虚线表示主压应力迹线。 xy主应力迹线的画法：11截面22截面33截面44截面ii截面nn截面bacd1313 sto与σ3平行的斜截面上的应力可在σ1、σ2应力圆的圆周上找到对应的点。§8-4空间应力的应力状态分析—一点的最大应力与σ2平行的斜截面上的应力可在σ1、σ3应力圆的圆周上找到对应的点。与σ1平行的斜截面上的应力可在σ2、σ3应力圆的圆周上找到对应的点。 1).弹性理论证明，图a单元体内任意截面上的应力都对应着图b的应力圆上或阴影区内的一点。图a图b2).整个单元体内的最大切应力为：tmax结论—— 3)：整个单元体内的最大切应力所在的平面： 二、三向应力状态：——（广义虎克定律）++一、单向应力状态：§8-5广义胡克定律 三、、广义胡克定律的一般形式:可以证明主应力与主应变方向一致 广义胡克定律的应用——求平面应力状态下任意方向的正应变：aa+90求出,就可求得方向的正应变 例槽形刚体内放置一边长为a=10cm正方形钢块，试求钢块的三个主应力。F=8kN，E=200GPa,μ=0.3。解：1)研究对象：2)由广义虎克定律：正方形钢块 例：如图所示空心圆轴，外经D=120mm，内经d=80mm，E=2.0×105MPa，μ=0.28，ε450=2.0×10-4。求：m。解：1、取单元体2、广义胡克定律（应力与应变关系）3、外力的确定τx450mm=8504（Nm） 展开上式，并略去高阶微量：四、体积应变体积应变与应力分量间的关系:--平均应力。体积应变—单位体积的体积改变 形状改变比能:单元体的比能(单位体积储存的变形能)：利用广义虎克定律: 231图ammm图b231-m-m-m图c图b体积改变，形状不变；图c形状改变，体积不变。单元体的比能： —称为体积改变比能图c图b图a图C单元体的体积应变：单元体的比能＝体积改变比能(b)＋形状态改变比能(c)—称为形状改变比能所以图C单元体体积不变图a单元体的体积应变： ——称为形状改变比能或畸形能b图的体积应变比能：图c图b图a 强度理论：§8-6强度理论概念构件在静载荷作用下的两种失效形式：(1)脆性断裂：材料无明显的塑性变形即发生断裂，断面较粗糙，且多发生在垂直于最大正应力的截面上，如铸铁受拉、扭，低温脆断等。(2)塑性屈服（流动）：材料破坏前发生显著的塑性变形，破坏断面粒子较光滑，且多发生在最大切应力面上，例如低碳钢拉、扭，铸铁压。本章介绍常用的四个经典强度理论人们根据大量的破坏现象，通过判断推理、概括，提出了种种关于破坏原因的假说，找出引起破坏的主要因素，经过实践检验，不断完善，在一定范围与实际相符合，上升为理论（为了建立复杂应力状态下的强度条件，而提出的关于材料破坏原因的假设及计算方法）。 1.最大拉应力理论（第一强度理论）材料发生脆性断裂的主要因素是最大拉应力达到极限值－构件危险点的最大拉应力－极限拉应力，由单向拉伸实验测得§8-7四个经典强度理论莫尔强度理论强度条件断裂条件 2.最大伸长拉应变理论（第二强度理论）无论材料处于什么应力状态,只要发生脆性断裂,都是由于最大拉应变（线变形）达到极限值导致的。－构件危险点的最大伸长线应变－极限伸长线应变，由单向拉伸实验测得强度条件断裂条件即 无论材料处于什么应力状态,只要发生屈服,都是由于最大切应力达到了某一极限值。3.最大切应力理论（第三强度理论）－构件危险点的最大切应力－极限切应力，由单向拉伸实验测得屈服条件强度条件实验表明：此理论对于塑性材料的屈服破坏能够得到较为满意的解释。并能解释材料在三向均压下不易发生塑性变形或断裂的事实。 无论材料处于什么应力状态,只要发生屈服,都是由于单元体的最大形状改变比能达到一个极限值。4.形状改变比能理论（第四强度理论）－构件危险点的形状改变比能－形状改变比能的极限值，由单拉实验测得屈服条件强度条件实验表明：对塑性材料，此理论比第三强度理论更符合试验结果，在工程中得到了广泛应用。 强度理论的统一表达式：结论.四个强度理论可以概括地表达为：危险点处的三个主应力的组合≤轴向拉压的。主应力的组合可以从不同的强度理论得到。故通常将主应力的这种组合称为相当应力，用表示。 四个强度理论的使用范围：3、三向受压的应力状态：采用第三、第四强度理论（屈服破坏）1、一般情况下：脆性材料采用第一、第二强度理论（断裂破坏）；塑性材料采用第三、第四强度理论（屈服破坏）。2、三向受拉的应力状态：采用第一、第二强度理论（断裂破坏） 强度理论的应用——tsxxy使用条件：屈服破坏，。 （单位：MPa）405060例：求图示单元体第三强度理论的相当应力。解:1、主应力的确定2、相当应力的确定 3020单位：MPa例：求图示单元体第三、四强度理论的相当应力。解：1、主应力的确定2、相当应力的确定 例：已知铸铁构件上危险点的应力状态。铸铁拉伸许用应[]=30MPa。试：校核该点的强度。解：1、根据材料和应力状态确定失效形式，选择设计准则。2、确定主应力并进行强度计算1=29.28<[]=30MPa.结论：强度是安全的。1＝29.28MPa,2＝3.72MPa,3＝0脆性断裂，采用最大拉应力理论 例：如图所示工字型截面梁，已知〔σ〕=180MPa,[τ]=100MPa试：全面校核（主应力）梁的强度。F0.32m0.32mF=100kN88.611.4Z7100B解：1、画内力图100kN100kN32kNmxxMFs 例：如图所示工字型截面梁，已知〔σ〕=180MPa,[τ]=100MPa试：全面校核（主应力）梁的强度。F0.32m0.32mF=100kN88.611.4Z7100B2、最大正应力校核(上、下边缘处)3、最大剪应力校核(中性层处) 例：如图所示工字型截面梁，已知〔σ〕=180MPa,[τ]=100MPa试：全面校核（主应力）梁的强度。F0.32m0.32mF=100kN88.611.4Z7100B4、主应力校核（翼缘和腹板交界处）tsxxy 小结1、材料破坏的类型：脆性断裂；屈服破坏。2、材料破坏的主要因素：最大拉应力；最大拉应变；最大剪应力；最大形状改变比能。3、强度理论的概念：关于引起材料破坏主要因素的各种假说。4、研究的目的：能用简单的力学实验建立复杂应力状态的强度条件。一、基本概念重点 2、最大拉应变理论（第二强度理论）强度条件：3、最大剪应力理论（第三强度理论）强度条件：4、最大形状改变比能理论：（第四强度理论；均方根理论；歪形能理论；畸形能理论）强度条件：二、四种常用的强度理论1、最大拉应力理论（第一强度理论）强度条件：重点 三、结论：四、各种强度理论的使用范围——1、三向受拉的应力状态：采用第一、第二强度理论（断裂破坏）。2、三向受压的应力状态：采用第三、第四强度理论（屈服破坏）。3、其它的应力状态：脆性材料采用第一、第二强度理论（断裂破坏）；塑性材料采用第三、第四强度理论（屈服破坏）。 五、强度理论的应用——tsxxy使用条件：屈服破坏，。强度条件：六、莫尔强度理论：难点重点