材料力学课件 第七章弯曲变形1.ppt

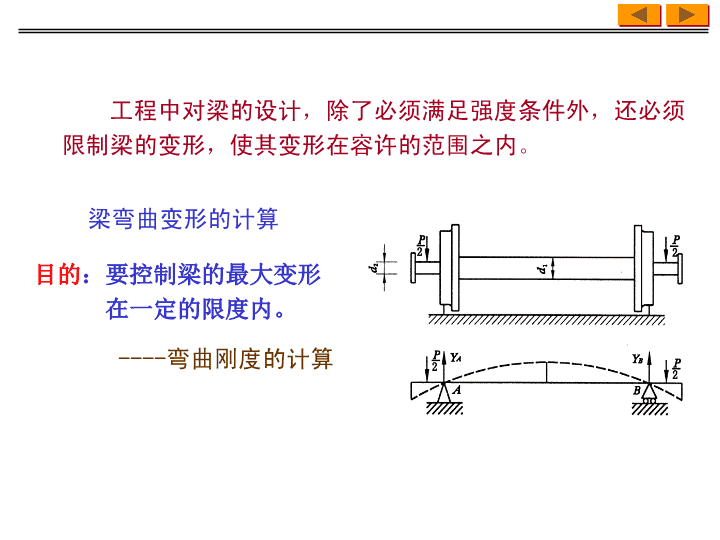
第七章弯曲变形§1梁变形的基本概念挠度和转角§2挠曲线近似微分方程§3积分法计算梁的变形§4叠加法计算梁的变形§5简单超静定梁 ----弯曲刚度的计算梁弯曲变形的计算目的：要控制梁的最大变形在一定的限度内。工程中对梁的设计，除了必须满足强度条件外，还必须限制梁的变形，使其变形在容许的范围之内。 梁的挠度，横截面的转角。度量梁变形的参数---二、挠度：横截面形心沿垂直于轴线方向的位移。一、挠曲线：梁变形后的轴线。性质：连续、光滑、弹性、极其平坦的平面曲线。三、转角：横截面绕中性轴转过的角度。用“”表示。q用“y”表示。q§7-1梁变形的基本概念挠度和转角x y=y（x）……挠曲线方程。挠度向下为正；向上为负。θ=θ(x)……转角方程。由变形前的横截面转到变形后，顺时针为正；逆时针为负。四、挠度和转角的关系挠度：横截面形心沿垂直于轴线方向的位移。转角：横截面绕中性轴转过的角度。用“”表示。用“y”表示。qq(挠曲线为一条平坦的曲线)x 一、曲率与弯矩的关系：EIM=r1二、曲率与挠曲线的关系（数学表达式)……（2）→→三、挠曲线与弯矩的关系：联立（1）、（2）两式得®……（1）§7-2梁的挠曲线近似微分方程qq M>00)(<¢¢xy挠曲线近似微分方程的近似性——忽略了“Fs”以及对变形的影响使用条件：弹性范围内工作的细长梁。M<00)(>¢¢xy结论：挠曲线近似微分方程——xyxy §7-3积分法计算梁的变形步骤：（EI为常量）1、根据载荷分段列出弯矩方程M（x）。2、根据弯矩方程列出挠曲线的近似微分方程并进行积分3、根据弯曲梁变形的边界条件和连续条件确定积分常数。右左CCqq=连续条件：右左CCyy=边界条件：F （1）、固定端处：挠度等于零、转角等于零。（2）、固定铰支座处；可动铰支座处：挠度等于零。（3）、在弯矩方程分段处：一般情况下左、右的两个截面挠度相等、转角相等。4、确定挠曲线方程和转角方程5、计算任意截面的挠度、转角；挠度的最大值、转角的最大值。1、根据荷载分段列出弯矩方程M（x）。2、根据弯矩方程列出挠曲线的近似微分方程并进行积分3、根据弯曲梁变形的边界条件和连续条件确定积分常数。积分法计算梁变形的步骤边界条件：连续性条件： 解：a)建立坐标系并写出弯矩方程例：求图示悬臂梁自由端的挠度及转角(EI=常数）。b)写出微分方程并积分c)应用位移边界条件求积分常数Fxd)确定挠曲线、转角方程e)自由端的挠度及转角x=0处:y(0)=0;q(0)=0yL qlABxC解：a)建立坐标系并写出弯矩方程b)写出微分方程并积分c)应用位移边界条件求积分常数d)确定挠曲线和转角方程e)最大挠度及最大转角ql/2ql/2x=0：y=0;x=l：y=0.例：求图示简支梁的最大挠度和最大转角(EI=常数） FC解：a)建立坐标系并写出弯矩方程b)写出微分方程并积分例：求图示梁的跨中的挠度和转角（EI=常数）左侧段（0≤x1≤a）：右侧段（a≤x2≤L）：AC段CB段 FC左侧段（0≤x1≤a）：右侧段（a≤x2≤L）：c)应用位移边界条件和连续条件求积分常数连续条件：y1(a)=y2(a),y’1(a)=y’2(a);边界条件：y1(0)=0,y2(L)=0b)写出微分方程并积分 FC左侧段（0≤x1≤a）：右侧段（a≤x2≤L）：d)确定挠曲线和转角方程 e)跨中点挠度及两端端截面的转角d)确定挠曲线和转角方程两端支座处的转角——FC跨中点挠度 梁上有分布载荷，集中力与集中力偶。弯矩：弯矩的叠加原理----梁在几个载荷共同作用下的弯矩值，等于各载荷单独作用下的弯矩的代数和。§7-4叠加法计算梁的变形 1、梁在简单载荷作用下挠度、转角应为已知或有变形表可查；2、叠加法适用于求梁个别截面的挠度或转角值。一、前提条件：弹性、小变形。二、叠加原理：各载荷同时作用下，梁任一截面的挠度或转角，等于各载荷分别单独作用下同一梁同一截面挠度或转角的代数和。三、叠加法的特征：叠加法计算梁的变形 aaF=+例：叠加法求A截面的转角和C截面的挠度.解:a)载荷分解如图b)由梁的简单载荷变形表，查简单载荷引起的变形。aaqFACAaaq aaF=+例：叠加法求A截面的转角和C截面的挠度.aaqFACAaaqc)叠加 =+L/2qFL/2ABC例：确定图示梁C截面的挠度和转角。解：1、载荷分解如图2、查梁的简单载荷变形表L/2qL/2L/2FL/2由F引起的C点位移：3、叠加 例利用叠加原理求图示弯曲刚度为EI的悬臂梁自由端B截面的挠度和转角。解：原载荷可看成为图a和b两种载荷的叠加，对应的变形和相关量如图所示。FlllEIFABCDqB1FqC1wC1yC1qC12l直线yB1(a)qD1qB2yD1·FqD1BD直线yD1yB2(b) 对图a，可得C截面的挠度和转角为：由位移关系可得此时B截面的挠度和转角为：（向下）（顺时针）FlllEIFABCDqB1FqC1wC1yC1qC12l直线yB1(a)qD2qB2yD2·FqD2BD直线yD2yB2(b) 对图b，可得D截面的挠度和转角为：同理可得此时B截面的挠度和转角为：（向下）（顺时针）FlllEIFABCDqB1FqC1wC1yC1qC12l直线yB1(a)qD2qB2yD2·FqD2BD直线yD2yB2(b) 将相应的位移进行叠加，即得：（向下）（顺时针）FlllEIFABCDqB1FqC1wC1yC1qC12l直线yB1(a)qD2qB2yD2·FqD2BD直线yD2yB2(b) 已知简支梁受力如图示，q、l、EI均为已知。求C截面的挠度yC；B截面的转角B1）将梁上的载荷分解yC1yC2yC32）查表得3种情形下C截面的挠度和B截面的转角。解 yC1yC2yC33）应用叠加法，将简单载荷作用时的结果求和 例:结构形式叠加（逐段刚化法)原理说明+y1=FFFFFy2 =+ABLaCqqaABLCM=qa2/2ÞÞ（b）例：求图示梁B截面的挠度（EI已知）。解：1)结构分解如图2)查梁的简单载荷变形表3)叠加BCÞÞq（a） 例：求图示梁C截面的挠度。解：1、结构分解如图2、查梁的简单载荷变形表L/2FL/2ABC2EIEIL/2FL/2ABC（a）=+L/2FL/2ABC（b）M=FL/23、叠加 例：拐杆如图，A处为一轴承，允许杆在轴承内自由转动，但不能上下移动，已知：E=210Gpa，G=0.4E，求B截面的垂直位移。分析：B点的垂直位移由：AB段弯曲和CA杆扭转而引起。FByB1FBACCMA=FLAByB2F 例、用叠加法求图示等截面直梁A、D、E（BC之中点）点的挠度。解：结构和载荷分解如图。E（1）（2）Fq=F/aF （4）FDCa（3）FFaFq=F/a