材料力学课件(哈工大)第4章 材料的力学性能,应力应变关系.ppt

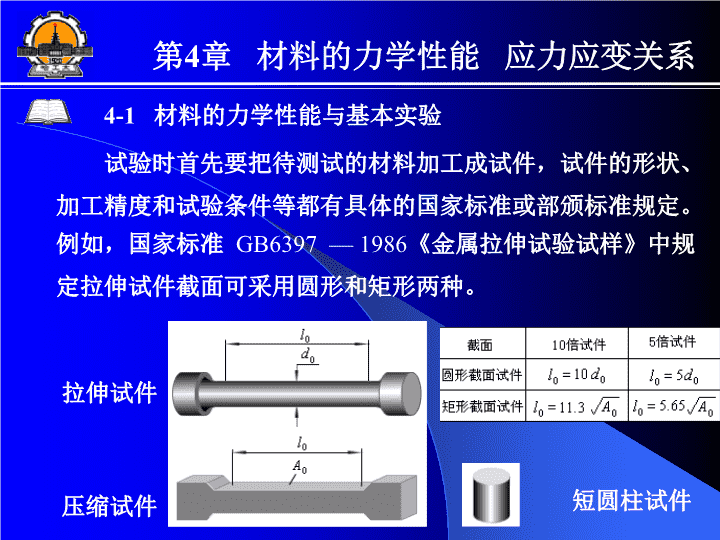
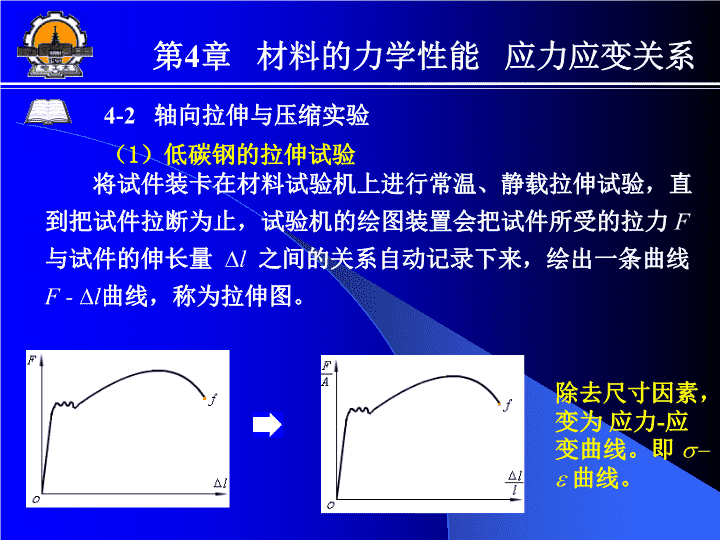
第4章材料的力学性能应力应变关系4-1材料的力学性能与基本实验材料在外力作用下所表现出的变形和破坏方面的特性，称为材料的力学性能。材料不同，其力学性能也不同。同一种材料，随着加载速率、温度等所处的工作环境的不同，其力学性能也不相同。本章只介绍材料在常温、静载、通常工作环境下的力学性能。最基本的实验是材料的轴向拉伸和压缩实验。 第4章材料的力学性能应力应变关系4-1材料的力学性能与基本实验试验时首先要把待测试的材料加工成试件，试件的形状、加工精度和试验条件等都有具体的国家标准或部颁标准规定。例如，国家标准GB6397—1986《金属拉伸试验试样》中规定拉伸试件截面可采用圆形和矩形两种。拉伸试件压缩试件短圆柱试件 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（1）低碳钢的拉伸试验将试件装卡在材料试验机上进行常温、静载拉伸试验，直到把试件拉断为止，试验机的绘图装置会把试件所受的拉力F与试件的伸长量l之间的关系自动记录下来，绘出一条曲线F-l曲线，称为拉伸图。除去尺寸因素，变为应力-应变曲线。即s-e曲线。 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（1）低碳钢的拉伸试验分析曲线，有几个特征点，把曲线分成四部分，说明低碳钢拉伸时，变形分为四个阶段。将试件装卡在材料试验机上进行常温、静载拉伸试验，直到把试件拉断为止，试验机的绘图装置会把试件所受的拉力F与试件的伸长量l之间的关系自动记录下来，绘出一条曲线F-l曲线，称为拉伸图。 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（1）低碳钢的拉伸试验第一阶段——弹性变形阶段（曲线ob段）在此阶段任一时刻时，将载荷慢慢减少（称卸载）为零，变形会消失。b点对应的应力称材料的弹性极限。即，材料处于弹性变形阶段时所能承受的最大应力，用表示，即 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（1）低碳钢的拉伸试验第一阶段——弹性变形阶段（曲线ob段）该阶段，曲线有很大一段是直线段（oa直线段），说明应力应变成正比关系，即E为比例常数，是材料的弹性模量，它反映了材料抵抗弹性变形的能力。胡克定律 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（1）低碳钢的拉伸试验第一阶段——弹性变形阶段（曲线ob段）a点对应的应力称材料的比例极限。即，材料应力应变处于正比例关系阶段时所能承受的最大应力，用表示，即 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（1）低碳钢的拉伸试验第二阶段——屈服（流动）阶段（曲线bc段）外力在小范围内波动，但变形显著增加。即，材料暂时失去了抵抗变形的能力。在此阶段某一时刻卸载为零，弹性变形消失，而还有一部分变形被永久地保留下来，称此变形为塑性变形。试件表面出现滑移线（与试件轴线成45度角度）。 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（1）低碳钢的拉伸试验第二阶段——屈服（流动）阶段（曲线bc段）曲线最低点所对应的应力，称为材料的屈服点，用表示，即 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（1）低碳钢的拉伸试验第三阶段——强化阶段（曲线ce段）过了屈服阶段，材料又恢复了抵抗变形的能力，称为强化。曲线最高点所对应的应力，称为材料的强度极限，用表示。强度极限是材料在整个拉伸过程中所能承受的最大应力，即 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（1）低碳钢的拉伸试验第四阶段——颈缩破坏阶段（曲线ef段）过了强化阶段，试件某一局部处直径突然变小，称此现象为颈缩。此后，试件的轴向变形主要集中在颈缩处。颈缩处试件横截面面积急剧减小，试件所承受的载荷也迅速降低，最后在颈缩处试件被拉断。 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（1）低碳钢的拉伸试验延伸率其中，是试件试验前的横截面面积;是颈缩处的最小横截面面积。其中，是试件包括塑性变形的长度，是试件试验前的长度。断面收缩率 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（1）低碳钢的拉伸试验冷作硬化现象经过弹性阶段以后，若从某点（例如d点）开始卸载，则力与变形间的关系将沿与弹性阶段直线大体平行的dd线回到d点。若卸载后从d点开始继续加载，曲线将首先大体沿dd线回至d点，然后仍沿未经卸载的曲线def变化，直至f点发生断裂为止。可见，在再次加载过程中，直到d点以前，试件变形是弹性的，过d点后才开始出现塑性变形。 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（1）低碳钢的拉伸试验冷作硬化现象比较这两个图形中的曲线，说明在第二次加载时，材料的比例极限得到提高（），而塑性变形和伸长率有所降低。在常温下，材料经加载到产生塑性变形后卸载，由于材料经历过强化，从而使其比例极限提高、塑性降低的现象称为冷作硬化。 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（2）铸铁的拉伸试验铸铁拉伸时，没有屈服阶段，也没有颈缩现象。铸铁的应力应变曲线没有明显的直线段，通常在应力较小时，取图上的弦线近似地表示铸铁拉伸时的应力应变关系，并按弦线的斜率近似地确定弹性模量E。反映强度的力学性能只能测得强度极限，而且拉伸时强度极限的值较低。由于铸铁的抗拉强度较差，一般不宜选做承受拉力的构件。抗拉强度差，这是脆性材料共同的特点。 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（3）低碳钢的压缩试验低碳钢试件压缩时的应力应变曲线。与拉伸曲线相比，屈服阶段以前曲线基本重合，即低碳钢压缩时，弹性模量E、屈服点均与拉伸时大致相同。过了屈服阶段，继续压缩时，试件的长度愈来愈短，而直径不断增大，由于受试验机上下压板摩擦力的影响，试件两端直径的增大受到阻碍，因而变成鼓形。压力继续增加，直径愈益增大，最后被压成薄饼，而不发生断裂，因而低碳钢压缩时测不出强度极限。 第4章材料的力学性能应力应变关系4-2轴向拉伸与压缩实验（4）铸铁的压缩试验与拉伸时相比，铸铁压缩时强度极限很高，例如，HT150压缩时的强度极限约为拉抻时强度极限的四倍。抗压强度远大于抗拉强度，这是铸铁力学性能的重要特点，也是脆性材料的共同特点。铸铁试件受压缩发生断裂时，断裂面与轴线大致成45的倾角，这表明铸铁试件受压时断裂是因最大切应力所致。 第4章材料的力学性能应力应变关系4-3没有明显屈服阶段的塑性材料工程中，有一类塑性材料，其应力应变曲线中没有明显的屈服阶段。例如，中碳钢、合金钢等。对于没有明显屈服阶段的塑性材料，通常人为地规定，把产生0.2%塑性应变时所对应的应力称为材料的屈服强度，并用表示。 第4章材料的力学性能应力应变关系4-4各向同性材料的广义胡克定律由材料的拉伸试验可知，在材料的比例极限范围内加载，受单向应力作用的一点，其正应力与线应变成正比，即实验表明，在比例极限内，横向（与应力垂直的方向）线应变（或）与纵向应变之比为一常量。用v表示这一比值的绝对值，则（1）简单胡克定律简单拉、压胡克定律 第4章材料的力学性能应力应变关系4-4各向同性材料的广义胡克定律由材料的拉伸试验可知，在材料的比例极限范围内加载，受单向应力作用的一点，其正应力与线应变成正比，即实验表明，在比例极限内，横向（与应力垂直的方向）线应变（或）与纵向应变之比为一常量。用v表示这一比值的绝对值，则（1）简单胡克定律简单拉、压胡克定律v称为横向变形系数或泊松比，是材料常数，其值可通过实验进行测定。 第4章材料的力学性能应力应变关系4-4各向同性材料的广义胡克定律由试验（扭转试验）还可指出，在材料的比例极限范围内，一点的切应力与相应的切应变成正比，即G称为材料的切变模量，其值与材料有关，可由实验测得。剪切胡克定律（1）简单胡克定律 第4章材料的力学性能应力应变关系4-4各向同性材料的广义胡克定律空间应力状态下，对于各向同性材料，在线弹性范围内，坐标轴方向的正应力只引起坐标轴方向的线应变，而不引起切应变；同样，各坐标面内的切应力只引起该坐标面内的切应变，而不引起线应变。由简单胡克定律，应用叠加原理，即（2）广义胡克定律（1）简单胡克定律 第4章材料的力学性能应力应变关系4-4各向同性材料的广义胡克定律（2）广义胡克定律同理得叠加得（1）简单胡克定律 第4章材料的力学性能应力应变关系4-4各向同性材料的广义胡克定律广义胡克定律（2）广义胡克定律据剪切胡克定律同理综上所述，对于原三向应力状态，有（1）简单胡克定律 第4章材料的力学性能应力应变关系4-4各向同性材料的广义胡克定律（2）广义胡克定律若单元体的三个主应力已知时，其广义胡克定律可写成（1）简单胡克定律 第4章材料的力学性能应力应变关系4-5应变能（1）体变应变与形状变形变形分为两类：体积变形与形状变形。单元体如果原是立方体，变形后仍为立方体，或单元体原是球体，变形后仍为球体。这种变形只是体积发生了变化，而形状没有变化，称为纯体积变形。如果原是立方体的单元体，变形后为体积相等的长方体，或原是球形单元体，变形后为体积相等的椭球体。这种变形只是形状发生了变化，而体积没有变化，称为纯形状变形。为方便起见，在主轴坐标系中进行考察。取一主单元立方体，变形前各棱边的长度均为da，则变形前体积变形后体积 第4章材料的力学性能应力应变关系4-5应变能代入广义胡克定律，得体变应变体变应变胡克定律其中平均应力体变应变弹性模量（忽略高阶微量）（1）体变应变与形状变形 第4章材料的力学性能应力应变关系4-5应变能体变应变各主应力1、2、3偏离平均应力m的量用s1、s2、s3表示，即s1=1-m，s2=2-m，s3=3-m。形状变形是由这些应力偏离量引起的。主单元体在主应力1、2、3作用下，不仅体积发生了变化，而且形状也发生了变化，由原来的立方体变为长方体。体变应变量是由单元体各面上平均应力引起的。形状变形（1）体变应变与形状变形 第4章材料的力学性能应力应变关系4-5应变能（2）应变能分析在弹性体变形过程的同时,外力要做功，并且转变为能量储存于该弹性体中。这种能量称为弹性变形势能，简称变形能。当逐渐卸去外力，弹性体又将所储存的变形能逐渐释放而做功，使变形逐渐消失。若外力增加十分缓慢时，可忽略弹性体内的动能及其他能量损失，可以认为外力功W全部转变为变形能，即轴向拉伸直杆，当拉力从零开始缓慢地增加到最终值F时，则杆的变形亦同时从零开始慢慢地增加到最终值l。在比例极限内，外力F与变形量l之间成正比关系，F—l图呈一过原点的斜直线单向应力状态下的应变能 第4章材料的力学性能应力应变关系4-5应变能（2）应变能分析在逐渐加力的过程中，当拉力为F1时，杆的变形量为l1，假如此时拉力再增加一个dF1，那么杆的变形将含有一增量d(l1)。于是已作用于杆件上的拉力F1因位移d(l1)而做功dW，就等于图中画阴影线部分的微分面积。单向应力状态下的应变能dW=F1d(l1)把最终的拉力F和最终的变形量l分别视为一系列dF1和d(l1)的积累，这样，拉力F所作的总功W便等于这些微分面积总和，即图中直线下三角形的面积。于是总功为整个杆件的变形能 第4章材料的力学性能应力应变关系4-5应变能（2）应变能分析储存在单元体内的变形能一般亦称应变能。单位体积中积蓄的应变能称为应变比能或应变能密度。单向应力状态下的应变能该图表示单元体受单向应力x作用，右图给出了相应的变形。单元体内的应变能密度将从杆件拉伸得到的结论应用于该单元体中，那么，x方向的力xdydz在x方向位移xdx上所做的功，即为储存在该单元体内的应变能，即 第4章材料的力学性能应力应变关系4-5应变能（2）应变能分析对于纯切应力状态，仿照上述分析，作用在单元体的上表面x方向的力，在x方向位移上所做的功，即为储存在单元体内的应变能，即单向应力状态下的应变能单元体内的应变能密度纯切应力状态下的应变能 第4章材料的力学性能应力应变关系4-5应变能（2）应变能分析在三向应力1、2、3作用下，变形固体内一点的应变能只与最终的力学状态（应力、应变）有关，与加载的历史（应力变化的历史）无关，故总应变能等于各应力分量分别在自己方向的应变上所做功的代数和。因此，相应的应变能密度为单向应力状态下的应变能代入广义胡克定律纯切应力状态下的应变能空间应力状态下的应变能总变形包括体积变形与形状变形，故而，总应变能密度e等于体变应变能密度和形变应变能密度的总和，即 第4章材料的力学性能应力应变关系4-5应变能（2）应变能分析体变应变能密度等于三个坐标轴方向的平均应力m在自己方向的应变m上所做功的代数和，即单向应力状态下的应变能纯切应力状态下的应变能空间应力状态下的应变能则，体变应变能密度为代入体变应变胡克定律则，形变应变能密度为或 第4章材料的力学性能应力应变关系4-6各向同性材料弹性常数之间的关系各向同性材料，材料常数E、v、G间存在如下关系考虑纯切应力状态，单元体只有形状变形，而无体积变形，形变应变能密度就是总的应变能密度。证明纯切应力状态为一种特殊的二向应力状态：1=xy，2=0，3=-xy，应用形变应变能密度表达式，得上两式右端相等，得证