已看组合变形材料力学课件

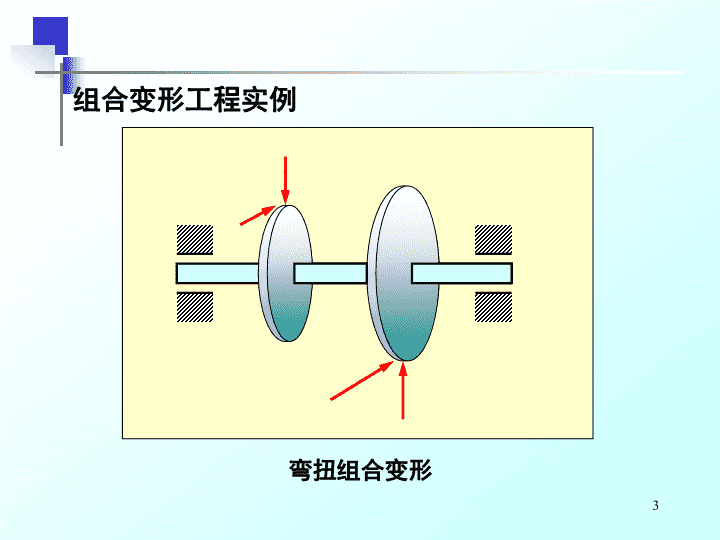
1压弯组合变形组合变形工程实例10-1第八章组合变形 2拉弯组合变形组合变形工程实例 3弯扭组合变形组合变形工程实例 4一、叠加原理构件在小变形和服从胡克定理的条件下，力的独立性原理是成立的。即所有载荷作用下的内力、应力、应变等是各个单独载荷作用下的值的叠加。 5二、处理组合变形的基本方法1、外力分析将外力简化并沿主惯性轴分解，将组合变形分解为基本变形,使之每个力(或力偶)对应一种基本变形3、应力分析画出危险截面的应力分布图，利用叠加原理将基本变形下的应力叠加,建立危险点的强度条件2、内力分析求每个外力分量对应的内力方程和内力图，确定危险截面。分别计算在每一种基本变形下构件的应力 6=++=+例压缩纯弯曲横力弯曲 7§8-1拉伸或压缩与弯曲的组合一、受力特点作用在杆件上的外力既有轴向拉(压)力，还有横向力二、变形特点杆件将发生拉伸(压缩)与弯曲组合变形 8FF1F2F1产生弯曲变形F2产生拉伸变形FyFxFy产生弯曲变形Fx产生拉伸变形示例1示例2 9内力分析xy0zMFN横截面上内力2、弯曲1、拉(压)：轴力FN弯矩M剪力因为引起的剪应力较小，故一般不考虑。 10横截面上任意一点(z,y)处的正应力计算公式为应力分析1、拉伸正应力2、弯曲正应力xy0zMFN(z,y)z单向应力状态z 11当材料的许用拉应力和许用压应力不相等时，应分别建立杆件的抗拉、抗压强度条件。强度条件由于危险点处的应力状态仍为单向应力状态，故其强度条件为（拉压等强度材料） 12例1桁架结构如图所示。横梁用20a工字钢制成。其抗弯截面模量Wz=237cm3,横截面面积A=35.5cm2，总荷载F=34kN，横梁材料的许用应力为[]=125MPa。校核横梁AB的强度。FACD1.2m1.2mB30° 13AB杆为平面弯曲与轴向压缩组合变形中间截面为危险截面。解：分析AB受力情况BADFFAyFAxFB30°FACD1.2m1.2m30°B(2)由内力图，确定危险截面最大压应力发生在该截面的上边缘(3)确定危险点 14压缩正应力最大弯曲压应力危险点的应力BADFFAyFAxFyFxFB30°FACD1.2m1.2m30°B所以结构安全 15例2：具有切槽的正方形木杆，受力如图。求：（1）m-m截面上的最大拉应力σt和最大压应力σc；（2）此σt是截面开槽前的σt值的几倍？ 16解：分析内力此σt是截面开槽前的σt值的8倍 17例3小型压力机的铸铁框架如图所示，立柱为T形截面。已知材料的许用拉应力[t]=30MPa，许用压应力[c]=160MPa。试按立柱的强度确定压力机的许可压力F。yzz0z15050150150 18解：(1)确定形心位置A=1510-3m2Z0=7.5cmIy=5310cm4截面对中性轴y的惯性矩yzz0z15050150150 19(2)分析立柱横截面上的内力和应力在n—n截面上有轴力FN及弯矩Myzz0z15050150150nn 20yzz0z150150150nn由轴力FN产生的拉伸正应力为由弯矩M产生的最大弯曲正应力为 21立柱横截面的最大应力(3)确定危险点的应力yzz0z150150150s¢ 22（4）求压力Fyzz0z150150150s¢分别由最大拉、压应力确定许可载荷 23LaABCF受力特点:杆件同时承受转矩和横向力作用变形特点:发生扭转和弯曲两种基本变形§8-2扭转与弯曲的组合 24一、内力分析研究AB杆的内力。将力F向AB杆右端截面的形心B简化得横向力F（引起平面弯曲）力偶矩m=Fa（引起扭转）AB杆为弯、扭组合变形BAFmxlaABCF 25画内力图确定危险截面固定端A截面为危险截面AAFmFaFl 26A截面C3C4TC3C4C2C1二、应力分析危险截面上的危险点为C1和C2点最大扭转切应力发生在截面周边上的各点处。C2C1危险截面上的最大弯曲正应力发生在C1、C2处AFmMT 27A截面对于许用拉、压应力相等的材料，可取任意点C1来研究。C1点处于平面应力状态TC3C4C2C1C3C4C2C1 28三、强度分析1、主应力计算2、相当应力计算第三强度理论,计算相当应力第四强度理论,计算相当应力 29该公式适用于图示的平面应力状态。是危险点的正应力，是危险点的切应力。横截面不限于圆形截面。讨论1. 30弯、扭组合变形时，相应的相当应力表达式可改写为对于圆形截面杆有式中W为杆的抗弯截面系数。M，T分别为危险截面的弯矩和扭矩.以上两式只适用于弯扭组合变形下的圆截面杆。2. 31例4传动轴如图所示，匀速转动。在A处作用一个外力偶矩m=1kN·m，皮带轮直径D=300mm，皮带轮紧边拉力为F1，松边拉力为F2。且F1=2F2，L=200mm，轴的许用应力[]=160MPa。试用第三强度理论设计轴的直径。zF1F2xyABl/2l/2m 32解：将力向轴的形心简化mm3F2zF1F2xyABl/2l/2m由平衡方程 33+T=1kN·m+中间截面为危险截面1kN·mmm3F2做内力图圆截面，弯、扭组合变形 34例5F1=0.5kN，F2=1kN，[]=160MPa。（1）用第三强度理论计算AB的直径。（2）若AB杆的直径d=40mm，并在B端加一水平拉力F3=20kN，校核AB杆的强度。F1F2ABCD400mm400mm400mm 35F1F2ABC400400m解:将F2向AB杆的轴线简化得AB为弯、扭组合变形F1F2ABCD400400400固定端截面是危险截面 36F3AB为弯，扭与拉伸组合变形固定端截面是危险截面(2)在B端加拉力F3F3F1F2ABC400400mF1F2ABCD400400400 37固定端截面最大的正应力为最大切应力为F3F3F1F2ABC400400mF1F2ABCD400400400由第三强度理论结构安全 38例6（重点）铸铁薄壁管，D=40，t=2。受P和T=PD/2作用。增大P使之破坏，破端面与轴线成84.4°，，按第一强度理论求破断时的P。PT100 39解：危险截面是固定端，内力：M=0.1PPT100T=PD/2=0.02P危险点位于其上边缘 40按第一强度理论，破断面应该是最大拉应力平面。故在面上出现解得P=1.49kN破端面与轴线成84.4° 41zP1P2xyAB8013080CD例7（重点）齿轮轴AB，n=265r/min。两轮传递功率P=10kN，直径D1=396mm，D2=168mm。啮合力与齿轮切线夹角为。轴直d=50mm，，校核强度。P1yP2zCD 42P1yP2zCDP1zP1yP2zP2yP1zP1yTCCP2zP2yTDD解：1.计算外力 43P1zP1yTCCP2zP2yTDDzP1P2xyAB8013080CDTCTDP1zP2zFBzFAzP1yP2yFByFAy分析轴的受力1.TC、TD使轴扭转2.4个y向力使轴在Oxy平面内弯曲3.4个z向力使轴在Oxz平面内弯曲 44TCTDP1zP2zFBzFAzP1yP2yFByFAyP1yP2zCDP1zP1yP2zP2y在Oxy平面内，求出在Oxz平面内，求出计算各力大小 45TCTDP1zP2zFBzFAzP1yP2yFByFAy2.画内力图My140Nm131NmMz133Nm264NmT361Nm1.由4个z向力在Oxz平面内做出My(矢量方向)图yzMy2.由4个y向力在Oxy平面内做出Mz(矢量方向)图Mz3.由TC和TD做出T图 46TCTDP1zP2zFBzFAzP1yP2yFByFAyMy140Nm131NmMz133Nm264NmT361Nm由图可知，危险截面可能在C或D截面，将弯矩合成。可见，危险截面是D截面。 473.校核强度轴由塑性材料制成，按第三或第四强度理论校核。变形是弯扭组合问题，圆截面杆件。所以所以轴安全。 484.最后一个问题D截面是危险截面，危险点在哪？Dyz危险点危险点