材料力学课件哈工大第16章压杆稳定

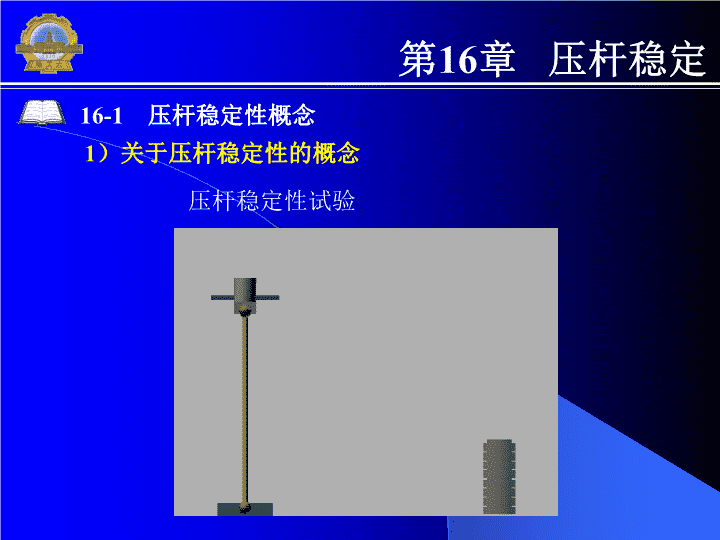
第16章压杆稳定16-1压杆稳定性概念1）关于压杆稳定性的概念工程中的压杆轴侧方向俯视方向 第16章压杆稳定16-1压杆稳定性概念压杆稳定性试验1）关于压杆稳定性的概念 第16章压杆稳定16-1压杆稳定性概念压杆稳定性试验表明，两端铰支均质等直细长杆，加轴向压力F，压杆呈直线形态平衡。若此压杆受到一很小的横向干扰力(例如，轻轻地推一下)，则压杆弯曲。当横向干扰力解除后，会出现下述两种情况：当轴向压力F小于某一数值时，压杆又恢复到原来的直线平衡形态。当轴向压力F增加到这一数值时，虽然干扰力已解除，但压杆不再恢复到原来的直线平衡形态，而在微微弯曲的形态下平衡。第一种情况表明压杆的直线平衡形态是稳定的；而第二种情况表明压杆的直线平衡形态是不稳定的。1）关于压杆稳定性的概念 第16章压杆稳定16-1压杆稳定性概念可见，压杆原来直线形态的平衡是否稳定，与所受的轴向压力F的大小有关；当轴向压力F由小逐渐增加到某一个数值时，压杆的直线形态平衡由稳定过渡到不稳定。压杆的直线形态平衡由稳定过渡到不稳定所受的轴向压力的界限值，称为压杆的临界力，用Fcr表示。当压杆所受的轴向压力F达到临界力Fcr时，其直线形态的平衡开始丧失，称压杆发生了稳定性失效，简称失稳。这是不同于强度失效的又一类构件失效问题。研究压杆稳定性的关键是寻求其临界力Fcr的值。1）关于压杆稳定性的概念 第16章压杆稳定16-2确定临界力的静力法欧拉公式1）两端铰支细长压杆的临界力假设两端球形铰支的等直细长压杆所受的轴向压力刚好等于其临界力，并且已经失稳而在微微弯曲状态下保持平衡。 第16章压杆稳定16-2确定临界力的静力法欧拉公式假设两端球形铰支的等直细长压杆所受的轴向压力刚好等于其临界力，并且已经失稳而在微微弯曲状态下保持平衡。令1）两端铰支细长压杆的临界力 第16章压杆稳定16-2确定临界力的静力法欧拉公式边界条件由式(f)、式(g)得只有1）两端铰支细长压杆的临界力 第16章压杆稳定16-2确定临界力的静力法欧拉公式由式(j)、式(c)得式(k)表明,使压杆保持曲线形态平衡的压力，在理论上是多值的。而在这些压力中，使压杆保持微微弯曲的最小轴向压力，才是其临界力。故1）两端铰支细长压杆的临界力 第16章压杆稳定16-2确定临界力的静力法欧拉公式取n=1，得欧拉公式在此临界力作用下，，则式(e）可写成1）两端铰支细长压杆的临界力 第16章压杆稳定16-2确定临界力的静力法欧拉公式由式(l)可见，两端铰支细长压杆失稳后，挠曲线是一条半波正弦曲线。最大挠度与轴向压力F间的理论关系曲线，即压杆的平衡路径。曲线表明，当压杆所承受的轴向压力F小于临界力时，F与间关系为直线OA，说明压杆只有直线这一种平衡形态，直线平衡形态是稳定的。当轴向压力F大于临界力时，压杆既可在直线形态（AF）下保持平衡，也可在曲线形态下（AB）保持平衡，但前者是不稳定的，后者是稳定的。1）两端铰支细长压杆的临界力 第16章压杆稳定16-2确定临界力的静力法欧拉公式直线AF与曲线AB的交点A称为平衡路径的分叉点，说明从该点开始，压杆出现两种平衡形态。但是，实际压杆并非理想压杆，这些与理想压杆不相符合的因素，可相当于作用在压杆上的压力与压杆轴线有一个微小的偏心距。实验结果表明，实际压杆的F与间关系如图中的曲线OD所示。偏心距越小，曲线越接近OAB。以上讨论的均假设压杆轴线是理想直线，压力是轴向压力，压杆材料均匀连续。这是理想情况，称为理想压杆。1）两端铰支细长压杆的临界力 第16章压杆稳定16-2确定临界力的静力法欧拉公式以一端固定、一端自由长为l的压杆为例在其他约束情况下，可用上述静力法求临界力，也可用如下简捷的方法求临界力。2）不同杆端约束细长压杆的临界力工程中的压杆，两端会有各种不同的约束。从上述推导临界力的过程可看出，约束条件不同，压杆的临界力也不同，即杆端约束对临界力有影响。以固定端B为对称点向下延长至。延长后的挠曲线是一条半波正弦曲线，与两端铰支压杆失稳后的挠曲线形状一样。1）两端铰支细长压杆的临界力 第16章压杆稳定16-2确定临界力的静力法欧拉公式用这种比较失稳后挠曲线形状的方法，同样会得到其他约束情况下压杆的临界力公式，这些公式可统一写成这样就比拟得到，一端固定、一端自由长为l的压杆的临界力与两端铰支长为2l压杆的临界力相同，即欧拉公式的一般形式m称为长度系数，可查手册；ml称为压杆的相当长度。2）不同杆端约束细长压杆的临界力1）两端铰支细长压杆的临界力 第16章压杆稳定16-3超过比例极限压杆的临界力计算将式(16-2)的两端同时除以压杆的横截面面积A，得到压杆的临界应力应力形式的欧拉公式因为这样式(a)可写成其中称为压杆的柔度 第16章压杆稳定16-3超过比例极限压杆的临界力计算推导欧拉公式时，曾使用了挠曲线的近似微分方程式。而这个方程式是建立在材料服从虎克定律基础上的。试验已证实，当临界应力不超过材料的比例极限时，由欧拉公式得到的理论曲线与试验曲线十分相符；而当临界应力超过时，两条曲线随着柔度减小相差愈来愈大。这说明欧拉公式只有在临界应力不超过材料的比例极限时才适用，即于是当时，欧拉公式成立。令称为与材料比例极限相对应的柔度值。满足条件的压杆，称为细长杆。或 第16章压杆稳定16-3超过比例极限压杆的临界力计算对于超过材料比例极限压杆的稳定性问题，曾进行过许多理论和实验研究工作，得出了较多的分析结果。但目前工程中普遍采用的是一些以实验为基础的经验公式。常用的经验公式有直线公式和抛物线公式。对于很小柔度的短压杆，当它所受到的压应力达到压缩极限应力时，压杆已因强度不足而失效。故，直线公式也有适用范围，即其中，a、b均为材料常数，可查材料手册得到。直线公式塑性材料脆性材料 第16章压杆稳定16-3超过比例极限压杆的临界力计算于是，当时，直线公式成立。满足此条件的压杆，成为中长杆。塑性材料脆性材料或令称为与材料屈服点相应的柔度值综上所述，当强度问题 第16章压杆稳定16-3超过比例极限压杆的临界力计算为材料常数，可查手册。直线公式抛物线公式（略）压杆的临界应力随着压杆的柔度变化情况可用曲线表示，此曲线称为临界应力总图。综上所述采用直线公式时采用抛物线公式时 第16章压杆稳定16-4压杆的稳定性计算稳定性条件许用的稳定安全系数所承受的实际轴向压力工作时的稳定安全系数稳定性计算结构设计校核稳定性计算许可载荷