[工学]吉林大学材料力学课件

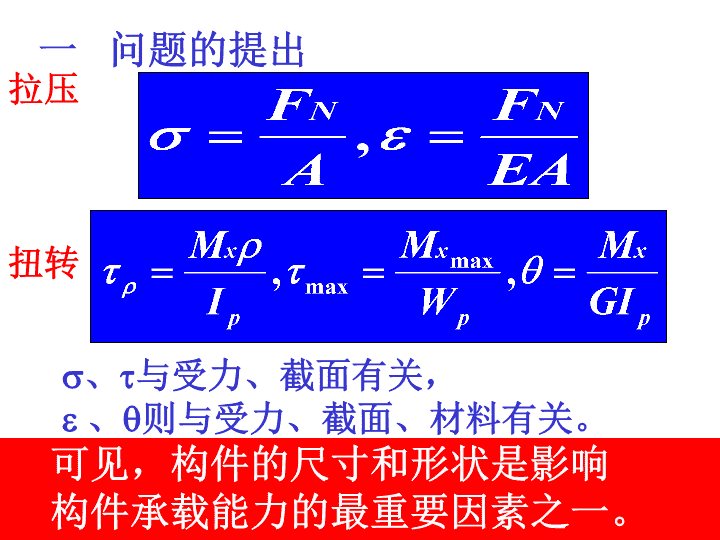
§A.1静矩和形心§A.3平行移轴公式附录A平面图形的几何性质§A.4转轴公式、主惯性矩§A2惯性矩、惯性半径、惯性积 一问题的提出拉压扭转、与受力、截面有关，、则与受力、截面、材料有关。可见，构件的尺寸和形状是影响构件承载能力的最重要因素之一。 二什么叫平面图形的几何性质？事实表明，对弯曲而言，其应力不仅与截面的大小、形状有关；而且还与截面如何放置有关，所以要全面研究平面图形的几何性质。横截面平面图形式中AIPWp均为与横截面大小和形状有关的几何量.``` 一静矩——面积对轴之矩定义：§A.1静矩和形心dAoyzcyzyz 二、形心可根据静矩确立形心坐标：1量纲：长度32S与面积的大小、分布均有关3与参考轴的位置有关讨论4S=0轴过形心〈〉 例A–1求直径为d的半圆形的形心解:取Z轴为对称轴zdyczdz 三、组合图形的静矩和形心静矩：,iiyzASS=iizyASS=iiiAzAzSS=iiiAyAySS=,形心： 例A-2求形心坐标0=yzy2)2(22112221211+++=tbtbbtbtbtbb2b1z1zz2iiiAzAzSS=t1t2 一、惯性矩定义：§A.2惯性矩、惯性半径、惯性积yzozy特点：1、I恒大于02、量纲：长度4 二、惯性半径定义：yzoA 三、极惯性矩定义：yzozydA z1y1oyz结论：图形对任意一对互相垂直的惯性矩之和等于它对该两轴交点的极惯性矩。 四、惯性积定义：1.量纲:长度42.Iyz＞＝＜0dAcoyzyzyz 惯性积一定是对一对互相垂直坐标轴而言。注意特点：两个坐标轴中只要一个为图形的对称轴，则必有yz 五、常用图形、i的计算cyz同理：例A-3已知h和b，求zbh解: oyzd解:例A-4已知直径d,求 oyz解:`例A-5已知直径Dd,求 §A.3平行移轴公式上式中的三个积分为：oyzcycyzczbayczc 由以上关系可知注意1．两对轴必为平行轴；2．必有一对是形心轴；3．a、b有正、负； 结论：对所有平行轴而言，对形心轴的惯性矩取最小值。应用:1可计算平行轴的惯性矩、惯性积；2可计算组合图形的惯性矩、惯性积。 例A－６已知b,h,求oyzbhc解: 例A-7求解：取通过矩形II的形心且平行于底边的参考轴y,则2014010020cyzcycz 形心位置确定后，使用平行移轴公式分别算出矩形I和矩形II对yc轴的惯性矩，即 所以，整个图形对yc轴的惯性矩应为 §A.4转轴公式主惯性矩oyzdAy1zyy1z1（I）公式推导：z1已知IyIzIyz，````求 和代入上式，得把 同理 （II）几个概念：1主轴--惯性积等于零的一对轴2主惯性矩--对主轴的惯性矩3形心主轴--过形心的主轴4形心主惯性矩--对形心主轴的惯性矩可以看出：主惯性矩平面图形对坐标原点不变的任何一对正交轴的惯性矩之和为一常数，即（常数）极值惯性矩 小结1轴轴关系对称轴（过形心，）形心轴（过形心）主惯性轴（）形心主惯性轴 2轴面关系（1）形心---一个.c.c（3）主轴---一般情况过一点只有一对，整个截面上有无穷对。（2）形心轴---无穷个 （4）形心主轴---一般情况下一个截面只有一对，特殊情况下一个截面有无穷对。（一对）（多于一对） 可以证明：任何一个形心轴都是形心主具有三个以上对称轴的截面，惯性轴，而且对这些轴的惯矩均相等。.c.c