材料力学课件第六章弯曲应力

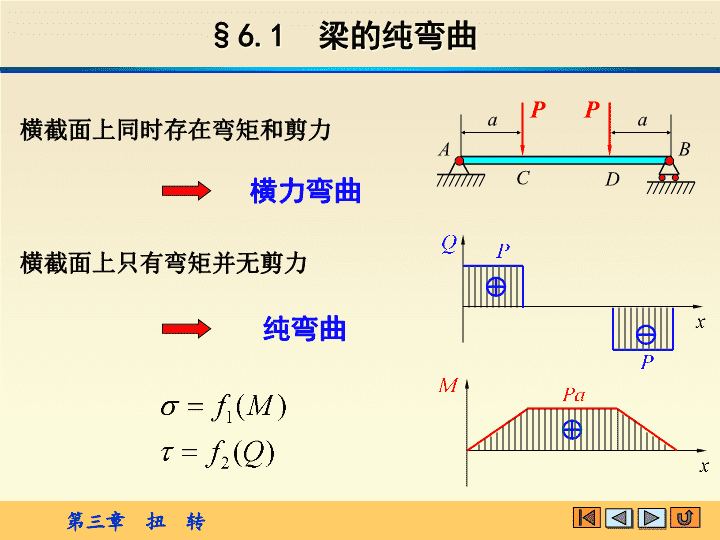
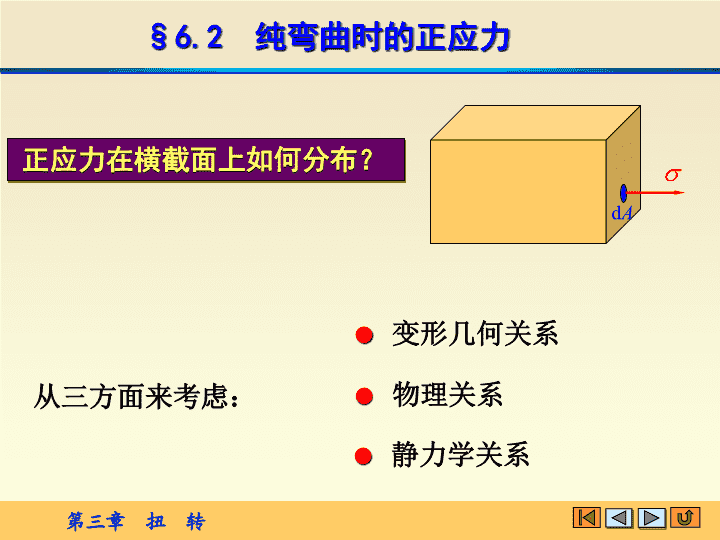
第6章弯曲应力※梁的纯弯曲※纯弯曲时的正应力※横力弯曲时的正应力※弯曲切应力※提高弯曲强度的措施 §6.1梁的纯弯曲PPaaABCD纯弯曲横力弯曲横截面上同时存在弯矩和剪力横截面上只有弯矩并无剪力 §6.2纯弯曲时的正应力dA正应力在横截面上如何分布？从三方面来考虑：变形几何关系物理关系静力学关系 1.变形几何关系 梁在纯弯曲时的平面假设：梁的各个横截面在变形后仍保持为平面，并仍垂直于变形后的轴线，只是横截面绕某一轴旋转了一个角度。 中性层：梁中纤维即不伸长也不缩短的那层。中性轴：中性层与横截面的交线。：中性层的曲率半径。 距中性层为y处的纤维的线应变： 再作单向受力假设：假设各纵向纤维之间互不挤压。2.物理关系 3.静力学关系M 中性轴过形心令: 横截面应力分布: 中性层的曲率公式:正应力计算公式:应用条件:中性轴过横截面的形心结论: 1.静矩和形心一、静矩分别为图形对z轴和y轴的静矩。zyOdAyzCyCzC由平面图形的形心公式:二、形心轴过形心对该轴静矩为零附录 Ozyydy计算由抛物线、y轴和z轴所围成的平面图形对y轴和z轴的静矩，并确定图形的形心坐标。例题1解：取微分面积如图示 OzyCyCzC 三、组合图形的静矩和形心1、组合图形对某一轴的静矩等于组成它的各部分图形对同一轴静矩的代数和，即：其中：Ai，yi，zi分别代表第i个图形的面积和形心坐标，n为分割成的简单图形的个数。2、组合图形的形心坐标 例题2求所示图形的形心位置解：建立图示坐标系，并将图形分成两部分。1002014020xy②①由于z轴是对称轴 求图示红色部分的面积对y轴的静矩。例题3bya解： 2.惯性矩和惯性半径一、惯性矩定义：图形面积对某轴的二次矩zyOdAyz其中iy、iz分别为平面图形对z轴和y轴的惯性半径。工程中常把惯性矩表示为平面图形的面积与某一长度平方的乘积,即或附录 其中iy、iz分别为平面图形对z轴和y轴的惯性半径。（4）组合图形对某轴的惯性矩等于各组成图形对同一轴的惯性矩之和:（5）工程中常把惯性矩表示为平面图形的面积与某一长度平方的乘积,即或 二、极惯性矩定义：图形面积对某点的二次矩又zyOdAyz 求图示矩形对对称轴y、z的惯性矩。例题4byzzdz解：取微分面积如图示同理可得： 求图示圆平面对y、z的惯性矩。例题5Cyzd解：由上一章可知又 3.惯性积一、惯性积定义：图形对一对相互垂直的轴的矩如果所选的正交坐标轴中，有一个坐标轴是对称轴，则平面图形对该对坐标系的惯性积必等于零。OyzdAdAzyOdAyz附录 二、几个主要定义(1)主惯性轴当平面图形对某一对正交坐标轴y0、z0的惯性积Iy0z0=0时，则坐标轴y0、z0称为主惯性轴。因此，具有一个或两个对称轴的正交坐标轴一定是平面图形的主惯性轴。(2)主惯性矩平面图形对任一主惯性轴的惯性矩称为主惯性矩。 (3)形心主惯性轴过形心的主惯性轴称为形心主惯性轴。可以证明:任意平面图形必定存在一对相互垂直的形心主惯性轴。(4)形心主惯性矩平面图形对任一形心主惯性轴的惯性矩称为形心主惯性矩。 4.平行移轴公式yCzCzyOdAyCbyCazzC附录 yCzCzyOdAyCbyCazzC 平行移轴公式：yCzCzyOdAyCbyCazzC 求图示图形对其形心轴y的惯性矩。例题6③ ③①②③C解：（1）将图形分割为三部分（2）计算三部分对形心主惯性轴的形心惯性矩。（3）计算组合图形的形心惯性矩 试计算T形截面的形心主惯性矩。例题73003027050yzC1C2yCC解：（1）确定形心及形心主惯性轴。由对称性可知: 3003027050yzC1C2yCC（2）利用平行移轴公式，分别计算两部分对yc的惯性矩。 §6.3横力弯曲时的正应力强度计算上式是在平面假设和单向受力假设的基础上推导的，实验证明在纯弯曲情况下这是正确的。对于横力弯曲，由于剪力的存在，横截面产生剪切变形，使横截面发生翘曲，不再保持为平面。弹性力学精确分析结果指出：当梁的跨度大于梁的横截面高度5倍(即l>5h)时，剪应力和挤压应力对弯曲正应力的影响甚小，可以忽略不计。因此由纯弯曲梁导出的正应力计算公式，仍可以应用于横力弯曲的梁中。 强度计算zdzbh 强度条件为：对于脆性材料,由于其抗拉和抗压强度不等,则应分别校核: 两矩形截面梁，尺寸和材料的许用应力均相等，但放置如图(a)、(b)。按弯曲正应力强度条件确定两者许可载荷之比P1／P2＝？例题1ABlzhbz(a)(b) ABl解：hbz(a)(b) 已知：P=10kN，a=1.2m[σ]=10MPa，h/b=2试：选择梁的截面尺寸。例题2ABCDEPP3Paaaabh ABCDEPP3PaaaabhOxM解：由对称性，可得： 已知：l=1.2m,[σ]=170MPa，18号工字钢，不计自重。求：P的最大许可值。例题3ABlP解：作弯矩图 C已知：图示梁的截面为T形，材料的许用拉应力和许用压应力分别为［t］和［c］，则y1和y2的最佳比值为多少？例题4解： 已知：P1=8kN，P2=20kN，a=0.6m，IZ=5.33×106mm4[b]=240MPa，[bc]=600MPa，安全系数n=4。试：校核梁的强度。例题5aaaP1=8kNP2=20kNABCD10010020 aaaP1=8kNP2=20kNABCD10010020xM解：（1）作弯矩图由图可得危险截面弯矩：许用应力为： aaaP1=8kNP2=20kNABCD10010020xM截面C下边缘：故：满足强度要求截面A： §6-4弯曲剪应力和强度校核一、矩形截面梁的剪应力Pq(x)xdxQ假设:t(y)//截面侧边，并沿截面宽度均匀分布思考:能否假设t(y)沿截面高度均匀分布? QQNN+dN面积A1对中性轴z的静矩 Qzyy 二、工字形截面梁的切应力Bbt翼缘: Bbt腹板: 在翼缘上，有平行于Q的剪应力分量，分布情况较复杂，但数量很小，并无实际意义，可忽略不计。在翼缘上，还有垂直于Q方向的剪应力分量，它与腹板上的剪应力比较，一般来说也是次要的。腹板负担了截面上的绝大部分剪力，翼缘负担了截面上的大部分弯矩。 三、圆截面梁的剪应力下面求最大剪应力：yzQ 例6：圆形截面梁受力如图所示。已知材料的许用应力［］=160MPa，［］=100MPa，试求最小直径dmin。4m 4m解：由正应力强度条件：由剪应力强度条件： §6.5提高弯曲强度的措施弯曲正应力强度条件:合理安排梁的受力情况，以降低Mmax的值；采用合理的截面形状，以提高W的值，充分利用材料的性能。 一.合理安排梁的受力情况1.合理布置支座的位置x=0.207l，最大弯矩减小83% MM1.合理布置支座的位置 二.选择合理的截面形状W的值越大越有利从经济角度考虑A的值越小越经济综合考虑，系数较大，则截面较为合理 横截面尺寸沿着梁轴线变化的梁——变截面梁当梁的各横截面上最大正应力都等于材料的许用应力时——等强度梁。三.等强度梁的概念 解：由题意可知即:图示三种截面梁，材质、截面内Ｍmax、max全相同。求三梁的重量比。并指出哪种截面最经济。例题7dab2b 解：任取一微段为研究对象图示木梁，已知下边缘纵向总伸长为10mm，E=10GPa，求：载荷P的大小。例题82m2mABCP200300 dhb我国营造法中，对矩形截面梁给出的尺寸比例是h:b=3:2。试用弯曲正应力强度证明：从圆木锯出的矩形截面梁，上述尺寸比例接近最佳比值。例题9解： 若主梁和副梁材料相同，截面尺寸相同，则副梁的最佳长度a为多少？例题10解：主梁AB的最大弯矩副梁CD的最大弯矩由:ABCDP 谢谢使用