清华大学本校用理论力学课件3-3 虚位移.ppt

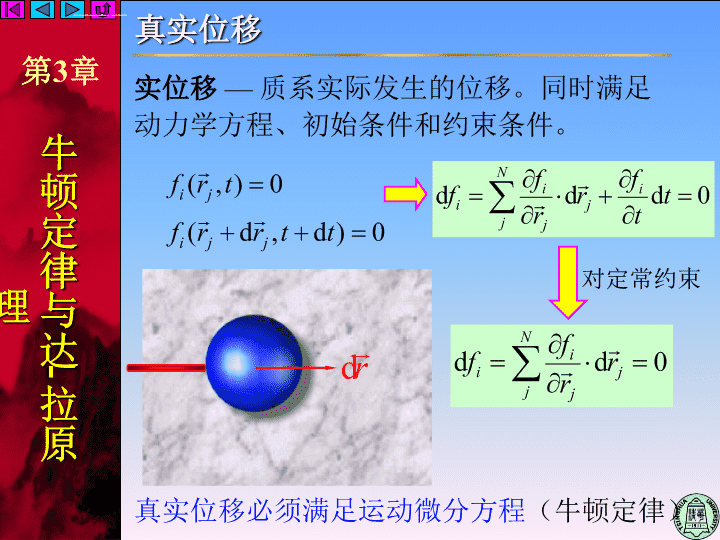
第3节虚位移 真实位移实位移—质系实际发生的位移。同时满足动力学方程、初始条件和约束条件。对定常约束真实位移必须满足运动微分方程（牛顿定律） 虚位移在给定瞬时，质系为约束所允许的、可能发生的无限小位移。用r表示。虚位移的发生不需要时间！ 实例分析虚位移有无穷多个！ 定常约束情况在定常约束情况下，实位移是无数虚位移之中的一个。真实位移虚位移实位移虚位移 非定常约束情况在非定常约束情况下，实位移不一定是无数虚位移中的一个。虚位移实位移 实例分析约束方程实位移虚位移虚位移质系虚位移的发生与时间t的变化无关(t0)，因此它就是约束被“冻结”后，质系在此瞬时为约束所允许的任意无限小位移。实位移 讨论虚位移只满足约束方程，实位移除满足约束方程外，还满足动力学方程。在定常约束情况下，实位移是无数虚位移中的一种，而在不定常约束情况下，实位移不一定是无数虚位移中的一种。非自由质点的虚位移垂直于约束曲面在该点的法线，即虚位移总是位于约束曲面的切平面 虚位移的方向约束方程虚位移MM1f=0在M1点返回 等时变分微分等时变分等时变分运算与微分运算类似，但t=0。将向径进行等时变分就是虚位移，将几何约束方程进行等时变分就可以得到虚位移之间的关系。 例1刚性杆等时变分 THEEND返回