【理论力学课件@北师大】10-4.pdf

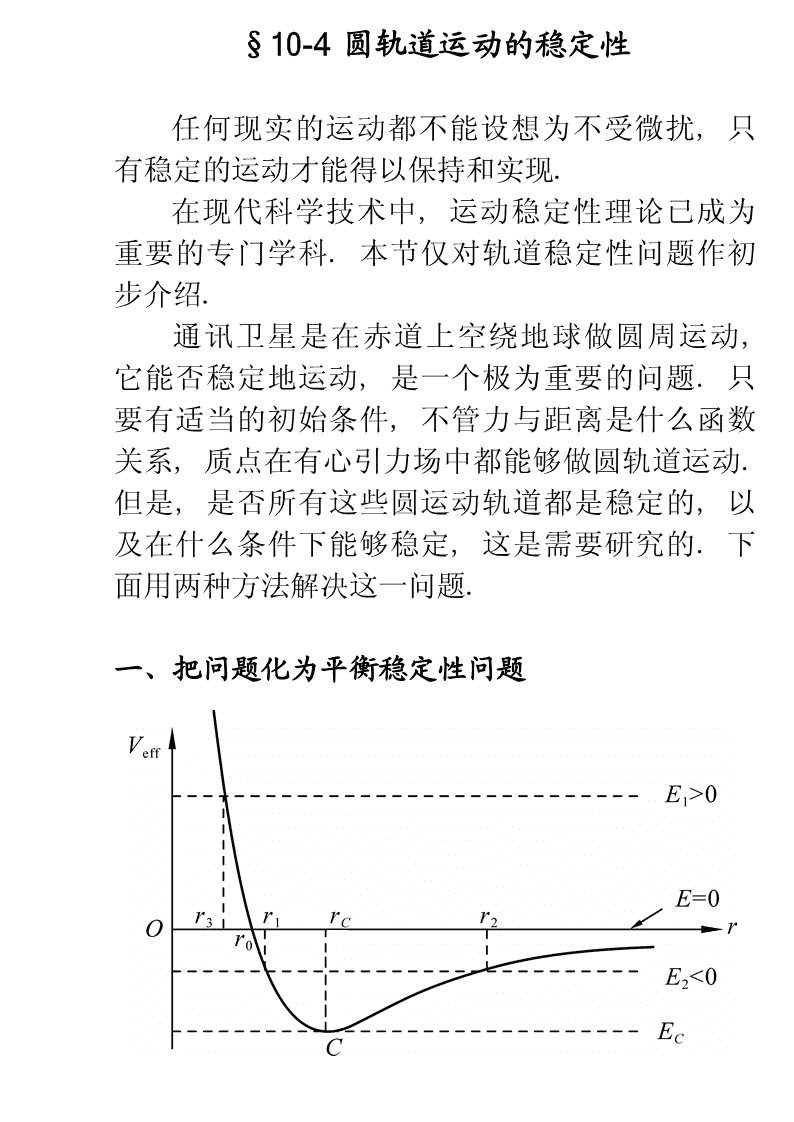
§10-4圆轨道运动的稳定性任何现实的运动都不能设想为不受微扰,只有稳定的运动才能得以保持和实现.在现代科学技术中,运动稳定性理论已成为重要的专门学科.本节仅对轨道稳定性问题作初步介绍.通讯卫星是在赤道上空绕地球做圆周运动,它能否稳定地运动,是一个极为重要的问题.只要有适当的初始条件,不管力与距离是什么函数关系,质点在有心引力场中都能够做圆轨道运动.但是,是否所有这些圆运动轨道都是稳定的,以及在什么条件下能够稳定,这是需要研究的.下面用两种方法解决这一问题.一、把问题化为平衡稳定性问题 2LV=V(r)+§10-1引入有效势能的概念eff2mr2§10-2中用有效势能的概念,把平方反比有心力场中二维运动化为一维运动,如图.可知,二维的圆运动化为一维的静平衡.通过平衡条件即有效势能取极值可求出平衡位置,也就是圆轨道的半径为r0(在图中rc),从极值条件得22dVdVLLeff=-=-F-=0drdrmr3rmr30现设引力的大小为F(r),则Fr=-F(r),代入上式后可知r0应满足方程2LF(r)-=00mr3(A)0L=mr2代入得mrq2=F(r),q是与半径r相将0q00000应圆运动的角速度.平衡的稳定条件就是圆运动的稳定条件,它要求有效势能在r0处具有极小值,即要求2d2V3Leff>0F¢(r)+>02r=r0即04drmr0将(A)式代入,得rdF0F(r)>-03drr=r0所以,欲使圆轨道运动稳定,F(r)必须满足上式. n让我们考察F(r)=kr的情况krk0>-(-n)rn3rn+100化简得n<3.说明只有当n<3时,圆轨道运动才是稳定的;当n³3时,圆轨道运动将是不稳定的.这个方法是严格正确的.二、微扰法质点以角速度q0,沿半径为r0的圆做匀角速运动——未扰运动,它们应满足动力学方程2mrq=F(r)000当质点受到一个小的扰动后,r和q都会在未扰运动上发生小的变化,即ìr=r+r¢0íq=q+q¢(A)î0其中r¢,q¢代表小的变化量,它们是时间的函数,我们认为它们是一阶小量.受扰后的运动应满足ìm(r-rq2)=-F(r)ír2q=r2qî00将(A)式代入上式,求出r¢,q¢满足的方程,研究它们的演化情况,若能始终保持为小量,则运动是稳定的;若有无限增大的行为,则运动是 不稳定的.2ìïm[r¢-()r+r¢(q+q¢)]=-F()r+r¢000íï()r+r¢2(q+q¢)=r2qî0000展开并忽略二阶以上的小量,同时,将函数f(r+r¢)在r附近作泰勒展开到一级,于是得00ìm[r¢-2rqq¢-r¢q2]=-dFr¢ïï000r=r0drí2r¢ïq¢=-q0ïrî0经线性化过程得到线性方程.好处——线性方程便于并能够求解.这是一种近似,只有当r¢和q¢取较小值时适用,当它发展变大到一定程度,线性方程不再适用.注意:线性方程与非线性方程是两种性质根本不同的方程,有时会得出与实际不符的结果.利用第二式消去第一式中q¢2dFm(r¢+3r¢q)=-r¢0r=r0dr22用mr0q0=F(r0)式消去上式中q0,得1édF3F(r)ù0ú¢r¢=-+rêr=r0mdrrë0û其中方括号内是一个数值,这数值的正负决定着r¢变化截然不同的性质.此方程是我们熟悉的 2r¢+wr¢=0因此,只有当1édF3F(r0)ù2+ú=w>0êr=r0mdrrë0û即rdF0F(r)>-03drr=r0时,方程才有振动解r¢=r¢cos(wt+a)0r¢才能保持为小量,从而运动具有稳定性.若dF3F(r)0+£0drr=r0r0则r¢将按指数规律或直线规律增长,运动是不稳定的.这些结果都与第一种方法得出的结果相同,但这一方法还能获得更多的信息,如果是稳定的话,给出了径向振动的圆频率;如果是不稳定的话,将得到r¢随时间按指数规律增长解,同一式子则给出r¢的增长率.