【理论力学课件@北师大】1-1.pdf

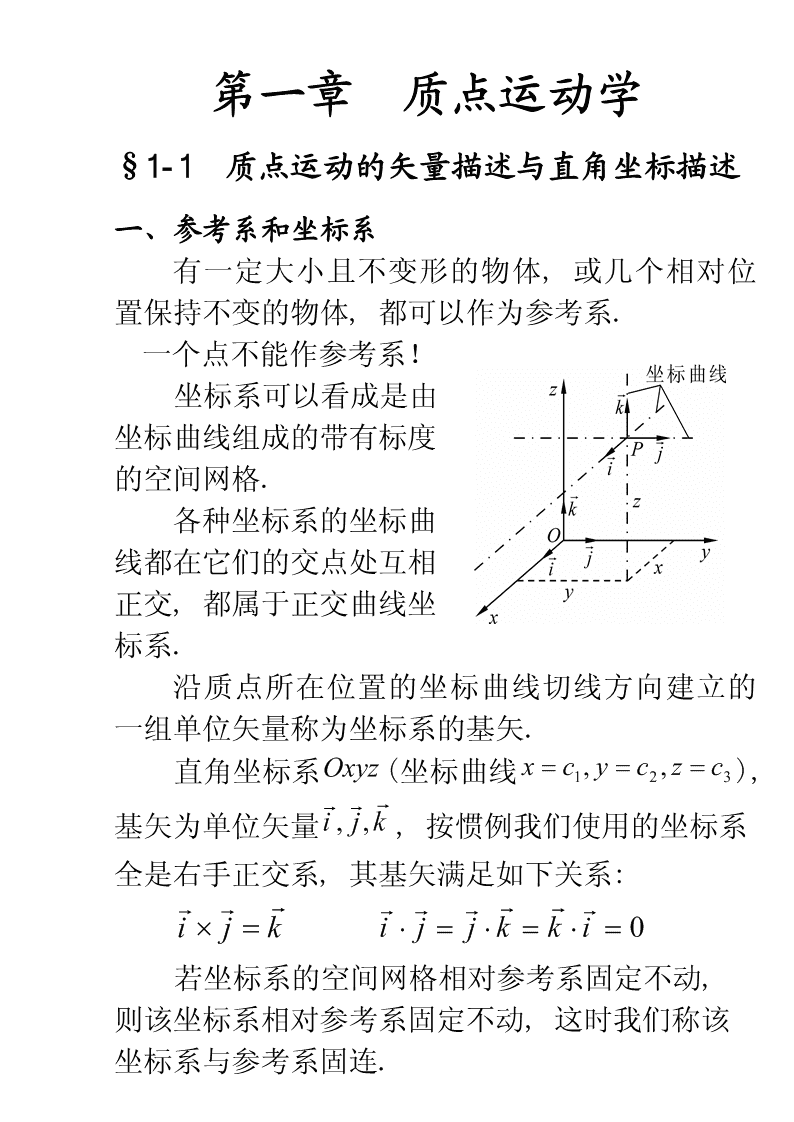
第一章质点运动学§1-1质点运动的矢量描述与直角坐标描述一、参考系和坐标系有一定大小且不变形的物体,或几个相对位置保持不变的物体,都可以作为参考系.一个点不能作参考系！坐标系可以看成是由坐标曲线组成的带有标度的空间网格.各种坐标系的坐标曲线都在它们的交点处互相正交,都属于正交曲线坐标系.沿质点所在位置的坐标曲线切线方向建立的一组单位矢量称为坐标系的基矢.直角坐标系Oxyz(坐标曲线x=c1,y=c2,z=c3),基矢为单位矢量i,j,k,按惯例我们使用的坐标系全是右手正交系,其基矢满足如下关系:i´j=ki×j=j×k=k×i=0若坐标系的空间网格相对参考系固定不动,则该坐标系相对参考系固定不动,这时我们称该坐标系与参考系固连. 二、自由度我们称确定力学系统位置所需要的独立坐标数为系统的自由度,自由度记为s.三、运动学方程和轨道图中我们用直角坐标系Oxyz代表参考系,位置矢量(简称位矢)r=rerr=r(t)称为质点的运动学方程,它包括了质点运动的全部信息.质点运动的轨道即为位置矢量r的矢端曲线.在直角坐标系Oxyz中r=xi+yj+zk运动学方程的分量形式为x=x(t),y=y(t),z=z(t)由式中消去时间t,则得到轨道方程.四、位移和路程位移是质点位置矢量的增量,Δr=r(t+Δt)-r(t)路程是质点沿轨道走过的长度,为一恒正标量,记为Ds,Ds=AB弧长. 注意Δr¹ΔsΔr¹ΔsΔr¹Δr但当Δt®0时,A,B间弦长与弧长相等,Dr®Ds,或记为dr=ds五、速度瞬时速度矢量简称为速度,被定义为位置矢量对时间的导数,Drdrv=lim==rDt®0Dtdt速度的方向沿轨道(即r的矢端曲线)的切线指向运动的前方,它的大小为速率v,Drdrdsv=v=lim===sDt®0Dtdtdt在直角坐标系Oxyz中,v=xi+yj+zk.六、加速度瞬时加速度矢量简称加速度,定义为速度对时间的导数, 2a=limDv=dv=v=dr=rDt®0Dtdtdt2加速度a一定指向轨道的凹侧.若将不同时刻的速度矢量的矢尾集中于一点,则可得出速度矢量v的矢端曲线即速端曲线.加速度a沿速端曲线切线方向并指向v的矢端沿速端曲线运动的前方,加速度的大小a等于v的矢端沿速端曲线运动的速率.任意矢量A对时间的导数A的方向沿A的矢端曲线的切线,其指向与A的矢端沿矢端曲线的运动方向一致;A的大小即A的矢端沿矢端曲线运动的速率.在直角坐标系Oxyz中,a=vi+vj+vk=xi+yj+zkxyz