【理论力学课件@北师大】10-5.pdf

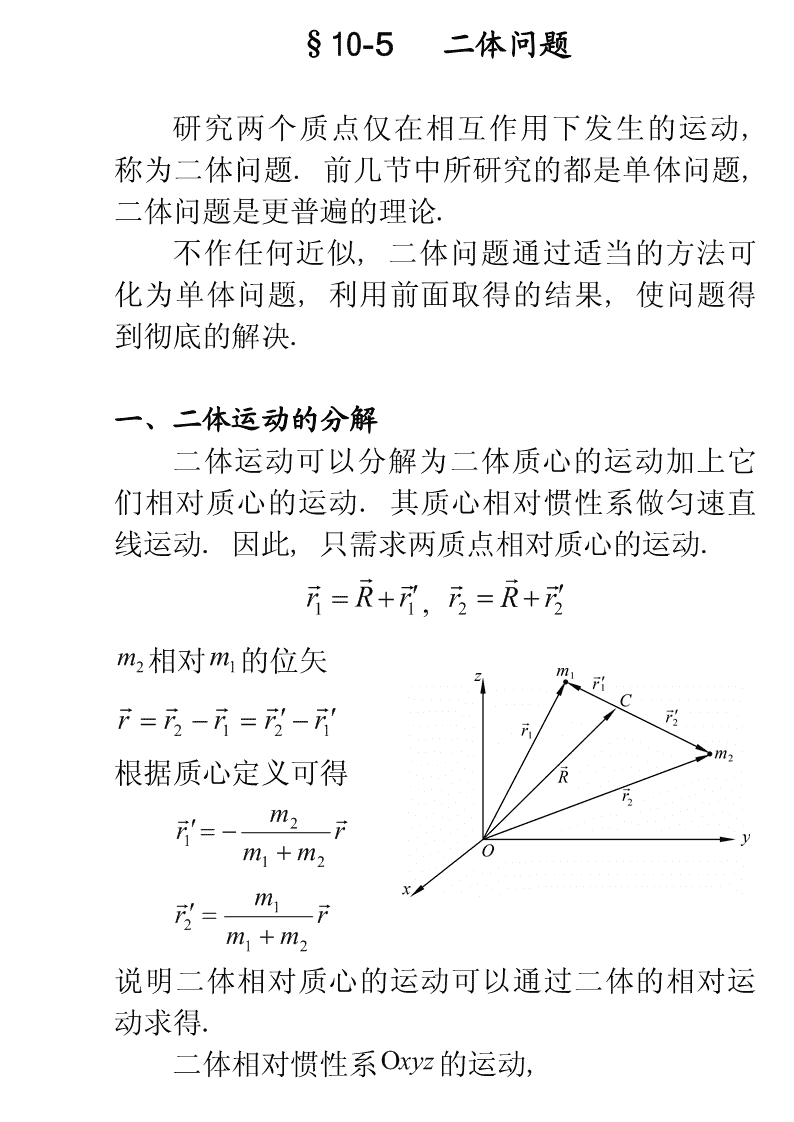
§10-5二体问题研究两个质点仅在相互作用下发生的运动,称为二体问题.前几节中所研究的都是单体问题,二体问题是更普遍的理论.不作任何近似,二体问题通过适当的方法可化为单体问题,利用前面取得的结果,使问题得到彻底的解决.一、二体运动的分解二体运动可以分解为二体质心的运动加上它们相对质心的运动.其质心相对惯性系做匀速直线运动.因此,只需求两质点相对质心的运动.r=R+r¢,r=R+r¢1122m相对m的位矢21r=r2-r1=r2¢-r1¢根据质心定义可得m2r¢=-r1m+m12m1r¢=r2m+m12说明二体相对质心的运动可以通过二体的相对运动求得.二体相对惯性系Oxyz的运动, ìm2r(t)=R()t-r()tï1ïm+m12ímïr¢=R()t+1r()t2ïm+mî12质心的运动由初始条件确定R(t)=R+vt0cR,v0c是质心的初位矢和初速度.剩下的问题是求二体的相对运动.二、二体的相对运动、约化质量现在来建立两体相对运动的方程.考虑一般情况,设质量为m2的质点受到的作用力为F,则二质点相对惯性系的运动方程为ìd2rd2rF11ïm12=-F®2=-ïdtdtmí1d2rd2rFïm222=F®22=ïdtdtmî2两式相减,得d2æ11ö()r-r=ç+÷Fdt221çmm÷è12ø若定义约化质量m为111mm12=+m=mmm或m+m1212则得m2相对m1的运动方程 2drm=F2dt这是质点m2相对于原点建立在m1上的平动坐标系的运动方程.此坐标系为非惯性系,相对它,牛顿第二定律应作修正,这个修正表现在质点所受的力中需补充惯性力,通过这种修正应能得到上式.上式说明修正的方法还可采取另一方式进行,即只要以约化质量代替原来的质量m2,在质点所受的力上就无需修正,这种方法带来很大的方便.二体问题化为单体问题!Gmmr12F=-2,其中m2不修正!rr如果m1>>m2,则m»m2,即质量不需要修正,意味着此时与m1一起运动的动坐标系可看做为惯性系.三、对开普勒第三定律的修正按二体问题考虑,太阳不是不动的,行星对太阳的运动方程应修正为2drGmsmm=-e22rdtrmmsm=m+ms于是 2drG(m+m)msm=-e22rdtr与认为太阳静止时行星的运动方程2drGmmsm=-e22rdtr进行比较,如果把右端仍看做为“万有引力”,这相当于太阳质量应修正为ms¢=ms+m.22T4p=将开普勒第三定律a3GM中的M=ms用m¢s替换,便得到修正后的开普勒第三定律22T4p=a3G()m+ms2T所以,严格说a3这一比值并不是对所有行星都相同,但实际上对太阳系九大行星来说,这比值的差别非常小,即使对质量最大的木星,两者质量之比msm=11047<<1,这种修正是非常小的.但是,对于质量相近的双星系统,则必须考虑修正.修正后的开普勒第三定律给我们提供了计算某些双星中一个星体的质量的依据.双星系统中可能有一颗星为暗星,可以根据二体理论,由亮星的运动导致暗星的发现.氢和重氢的核质量不同,电子在核外运动,考虑二体问题,则原子光谱有微小差异,由此导致了 重氢的发现.