【理论力学课件@北师大】11-4.pdf

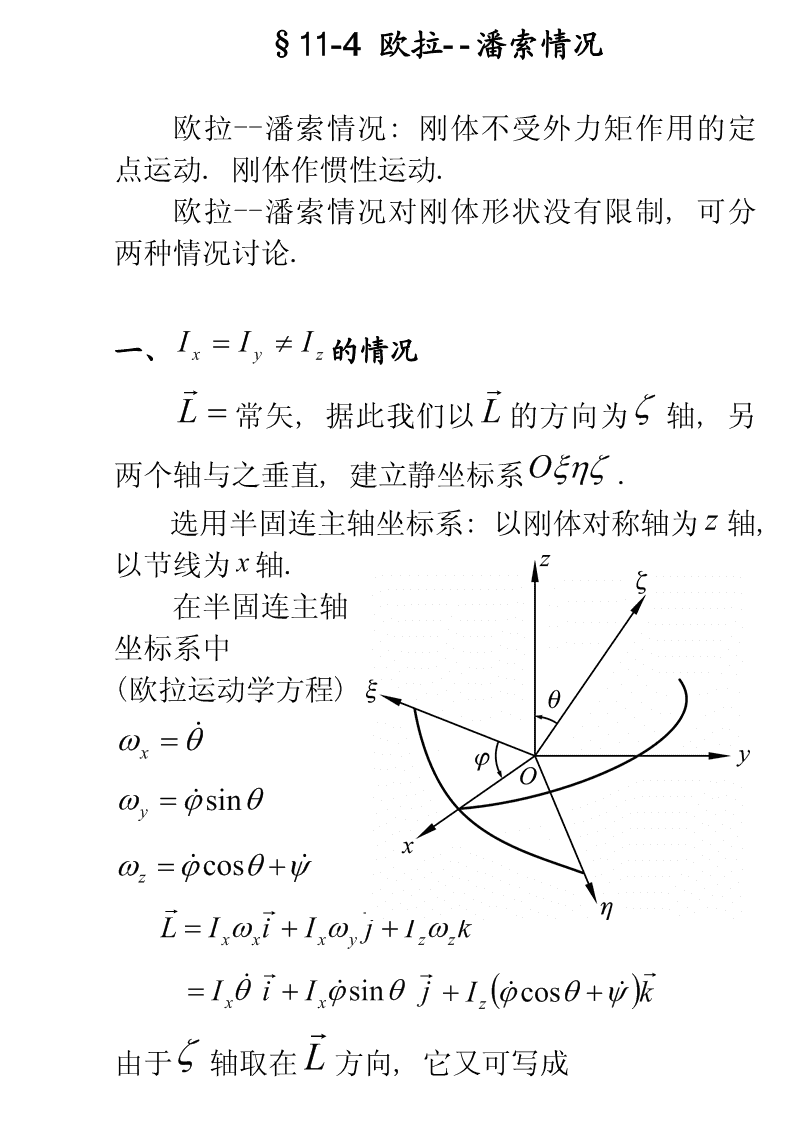
§11-4欧拉--潘索情况欧拉--潘索情况:刚体不受外力矩作用的定点运动.刚体作惯性运动.欧拉--潘索情况对刚体形状没有限制,可分两种情况讨论.一、Ix=Iy¹Iz的情况L=常矢,据此我们以L的方向为z轴,另两个轴与之垂直,建立静坐标系Oxhz.选用半固连主轴坐标系:以刚体对称轴为z轴,以节线为x轴.在半固连主轴坐标系中(欧拉运动学方程)w=qxw=jsinqyw=jcosq+yzL=Iwi+Iwj+Iwkxxxyzz=Iqi+Ijsinqj+I(jcosq+y)kxxz由于z轴取在L方向,它又可写成 L=Lsinqj+Lcosqk=常矢比较两式得出q=0®q=q0Lj=Ixæ11öy=ç-÷Lcosqç÷0IIèzxø刚体没有章动,而有均匀的自转和均匀的进动,这就是在Ix=Iy条件下,刚体绕定点的惯性运动的图象.这种运动又称为规则进动.*二、Ix¹Iy¹Iz的情况主轴坐标系必须与刚体固连,欧拉动力学方程为dwx()I-I-Iww=0xyzyzdtdwy()I-I-Iww=0yzxzxdtdwz()I-I-Iww=0zxyxydt此问题中存在的两个第一积分:角动量守恒和能量守恒 2222222Iw+Iw+Iw=Lxxyyzz222Iw+Iw+Iw=2Exxyyzz利用两个第一积分可以将其中两个变量,例如wy和wz,表为第三个变量wx的函数,将求得的两个表达式代入欧拉动力学方程中的第一式,使之化为wx的方程.解方程可用求积方法解决,但都需用椭圆函数表达.所以,欧拉动力学方程组虽是非线性的,但是可积的.利用欧拉运动学方程可求3个欧拉角随时间的变化关系.这种情况下刚体的惯性运动不仅有自转和进动,还有章动.例题4研究刚体绕主轴转动的稳定性.解此题是研究刚体不受外力矩作用的情况下,绕过定点的某一主轴做均匀转动的稳定性.设主轴为z轴,即未扰运动为:wx=0,wy=0,wz=w0(常量).扰动运动为:wx=w¢x,wy=w¢y,wz=w0+w¢z.初扰动wx¢0,w¢y0,wz¢0为小量.dwx()I-I-Iww=0xyzyzdtdwyI-()I-Iww=0yzxzxdt dwz()I-I-Iww=0zxyxydt第一式乘(Iz-Ix)wx,减去第二式乘(Iy-Iz)wy再积分可得()2()2II-Iw+II-Iw=常量xzxxyzyy即有22I(I-I)w¢+I(I-I)w¢xzxxyzyy22=I(I-I)w¢+I(I-I)w¢=常量xzxx0yzyy0可知这个常量为小量.如果Iz是3个主转动惯量中最大的一个或是最小的一个,则上式第一个等号左端两项是同号的,所以任何时候wx¢和w¢y都必须是小量.再利用能量守恒方程22()22Iw¢+Iw¢+Iw¢+w=2E=Iwxxyyzz0z0()22Iw¢+w»Iwzz0zo因此任何时候w¢z也必须是小量,从而证明绕主轴z轴的自由转动是稳定的.如果上述条件不满足,Iz不是3个主转动惯量中最大的一个或是最小的一个,而是取中间的值,则转动是不稳定的.