最优控制项目报告.doc

'最优控制项目报告—ProjectofOptimalControl二级倒立摆的控制黄自龙占奇志张晓电话：组号：第六组组员：黄自龙张晓：占奇志授课教师：高峰所在院、教研室：电气工程学院工企教研室考核形式：考试实验日期：2004.03.13～2004.05.188 一、问题的来源倒立摆的控制是控制理论应用的一个典型范例,一个稳定的倒立摆系统对于证实状态空间理论的实用性是非常有用的,倒立摆系统就其本身而言是一个非最小相位、多变量的系统.对于这样一个复杂系统的研究,从理论上需涉及系统的非线性、解耦、小时间常数及不稳定问题.控制理论的正确性及可行性需要一个按其理论设计的控制器去控制一个典型对象来验证，倒立摆正是一个典型的被控对象，世界上对倒立摆系统的研究一直在不断的进行。倒立摆作为一个研究对象有很多自身的特点，首先倒立摆本身是一个自然不稳定体，能反映出控制中的许多关键问题。如非线性问题、系统的鲁棒性问题、随动问题以及跟踪问题等。具体可以总结如下：1.作为实验装置，形象直观、结构简单，构件组成参数和形状容易改变。2.作为被控对象，相当复杂，是高阶次、多变量、非线性、强耦合系统。3.系统稳定效果非常明了，通过摆动角度、位移、稳定时间度量，控制好坏一目了然。4.重要的工程背景，倒立摆系统的稳定与机器人行走、空间飞行器控制有很大相似性。二、系统模型的建立一级倒立摆的建模与分析一级倒立摆的实际装置如图1所示：带轮小车顶端铰链系一刚性倒立摆，小车可沿有界轨道左右运动，摆可在垂直平面内自由运动。图1一级倒立摆模型各个参数的含义如下：X：小车的位移；：小车的速度；：摆杆偏离垂直方向的角度；摆杆的角速度；m0：小车的质量；m1：摆杆的质量；l1：摆杆的长度；g：重力加速度；F：控制器输出的控制力。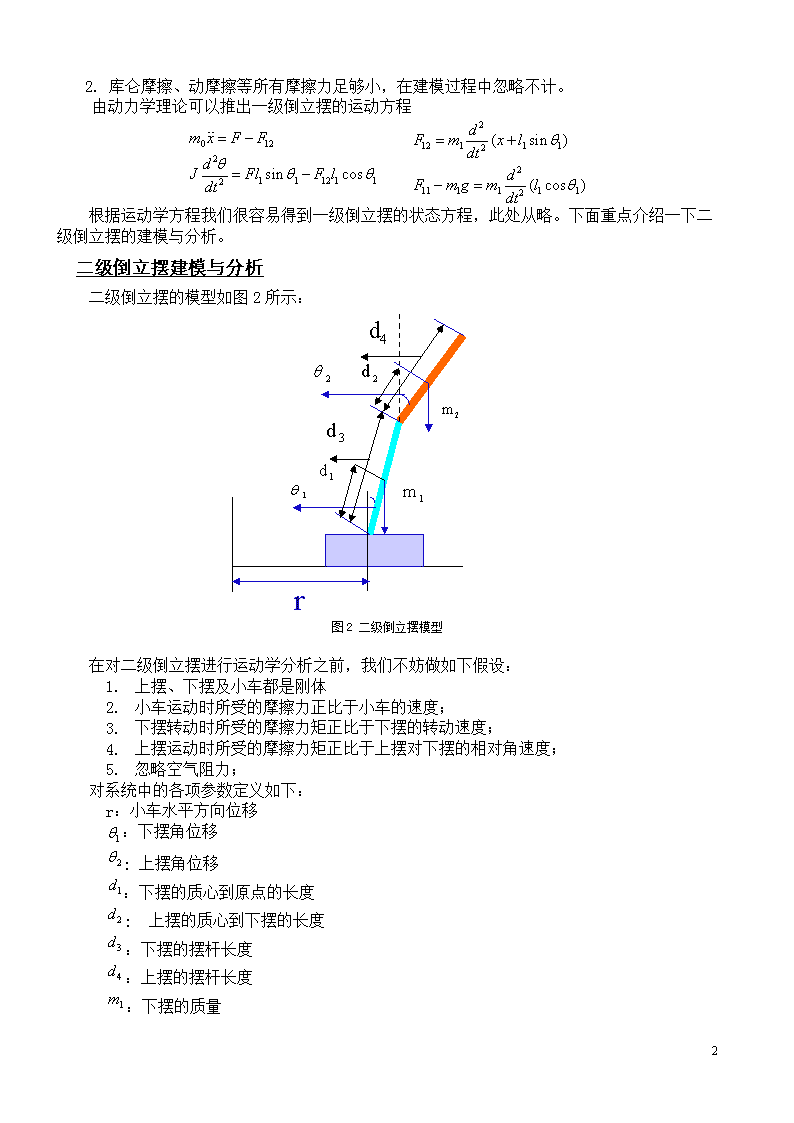我们做出如下假设条件：1.摆杆及小车都是刚体，8 1.库仑摩擦、动摩擦等所有摩擦力足够小，在建模过程中忽略不计。由动力学理论可以推出一级倒立摆的运动方程根据运动学方程我们很容易得到一级倒立摆的状态方程，此处从略。下面重点介绍一下二级倒立摆的建模与分析。二级倒立摆建模与分析二级倒立摆的模型如图2所示：lr图2二级倒立摆模型在对二级倒立摆进行运动学分析之前，我们不妨做如下假设：1.上摆、下摆及小车都是刚体2.小车运动时所受的摩擦力正比于小车的速度；3.下摆转动时所受的摩擦力矩正比于下摆的转动速度；4.上摆运动时所受的摩擦力矩正比于上摆对下摆的相对角速度；5.忽略空气阻力；对系统中的各项参数定义如下：r：小车水平方向位移：下摆角位移:上摆角位移：下摆的质心到原点的长度:上摆的质心到下摆的长度：下摆的摆杆长度：上摆的摆杆长度：下摆的质量8 ：上摆的质量：小车的质量用能量的观点对小车进行动力学分析，可以建立如下的能量方程：a)首先对小车进行分析小车的动能：小车的势能：小车损失的能量：b)下摆的能量学方程：动能：势能：损失的能量：c)上摆的能量学方程：动能：势能：损失的能量：令：设Lagrange函数（动势）：由Lagrange方程得：式中Qk——广义力;qk——广义坐标对Lagrange方程进行平衡点线性化并把方程改写成矩阵形式可以得到如下结果：8 定义状态向量，得到状态方程：3)二级倒立摆的控制策略(LQR)二级倒立摆的问题是一个二阶调节器问题，我们可以通过LQR算法来完成控制。图3二级倒立摆的控制模型图3的物理意义在于求得最优控制量u(t)使得系统在整个控制过程中的各个能量消耗的和最小，可以用Raccati方程求出最优控制的解。三．仿真建模及实验波形分析系统仿真根据上文对二级倒立摆模型的分析，结合提出的二次型目标函数，建立simulink模型如图4所示。图4二级倒立摆的simulink模型8 图中3个子模块分别实现描述小车加速度、上摆角加速度、下摆角加速度的三个状态方程。图中下方的K阵是Kalman增益，其中是Riccati方程的解。图5是用LQR方法建立的二级倒立摆系统的控制效果图。图中Y1是小车位移，Y2是图5二级倒立摆系统的控制效果图上摆的偏离角度，Y3是下摆的偏离角度。从图中可见各个被控量都能达到稳定状态。系统抗干扰能力检验为了检验所建立的二阶倒立摆系统模型的健壮性，考察状态变量的扰动对系统响应的影响。所加的扰动为周期10秒的脉冲群，每个脉冲持续时间为0.5秒幅值10度。图6为扰动加在上摆角度上时系统的响应，图7为相同的扰动加在上摆角度上时系统的响应。图6上加扰动时的系统响应8 图7上加扰动时的系统响应图6和图7分别仿真了当系统处于稳定状态时给上摆和下摆脉冲扰动时的响应，从图中可以看出，经过一段时间调节系统总能进入稳定状态。也证明了所建立的系统的健壮性，有较强的抗干扰能力。改变Q、R对系统响应的影响建立系统模型时二次型性能指标为，其中Q代表对各状态变量暂态误差的重视程度，R代表对消耗控制能量的重视程度。图8对小车位移最为重视8 图9对下摆角度最为重视图8所选用的Q=[100000000;010000;001000;000100;000010;000001];R=1。图9所选用的Q=[100000;010000000;001000;000100;000010;000001];R=1。图8小车位移的调整时间为2.5s幅值为0.03，图9小车位移的调整时间为10s，幅值为1。经过对比可见对小车位移的暂态误差更为重视的图8，小车位移的动态响应性能更优。R代表对消耗控制能量的重视程度，图10表示Q阵与图8一样，R分别为1和0.01时的系统响应图。由于状态变量不能明显的表示出控制能量的大小，又因为对于同一个二次型来说对某一个变量的重视程度增加，另一个量的重视程度就相对减弱，因此可以通过不同R时小车位移的动态响应来分析R对系统响应的影响。对比8、10两图，R=1时小车位移的调整时间为2.5s，幅值为0.03；R=0.01时小车位移的调整时间为2.5s，幅值为0.003。图10R=0.018 R=1相比与R=0.01来说对控制能量的消耗更为重视，从另一个角度看Q一样时，R=1对小车位移的相对重视程度比R=1时有所减弱，因此R=1时小车位移的调整时间比R=0.01时的长，小车位移也比R=0.01时来的更大。结论l通过倒立摆仿真实验表明,用最优控制器控制,系统具有较优的鲁棒性和瞬态特性.l控制性能与Q、R的选取相关四．致谢l由衷感谢高峰老师的指导；l感谢系统所冯祖仁老师研究生的指导；l特别感谢师兄师姐的帮助；l同时感谢同学们的热情无私帮助；参考文献[1].二级倒立摆控制策略的研究——基于状态反馈和T-S模型的控制,史晓霞,河北工业大学[2].二级倒立摆控制系统分析,李岩、姚旭东,沈阳工业学院学报1999年6月第18卷第2期[3].直线柔性连接两级倒立摆控制器设计,吴昊、秦志强等,华南理工大学自动化科学与工程学院[4].MATLAB帮助文件8'