隧道工程课程设计冯渔民

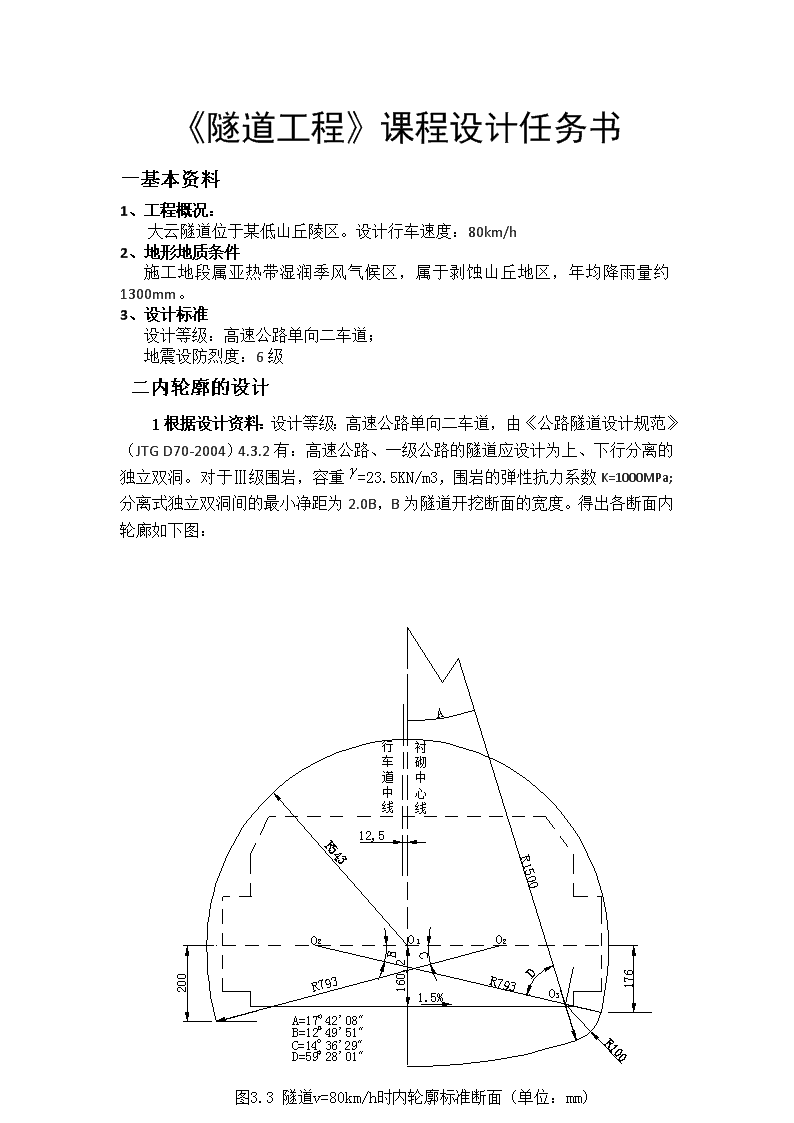
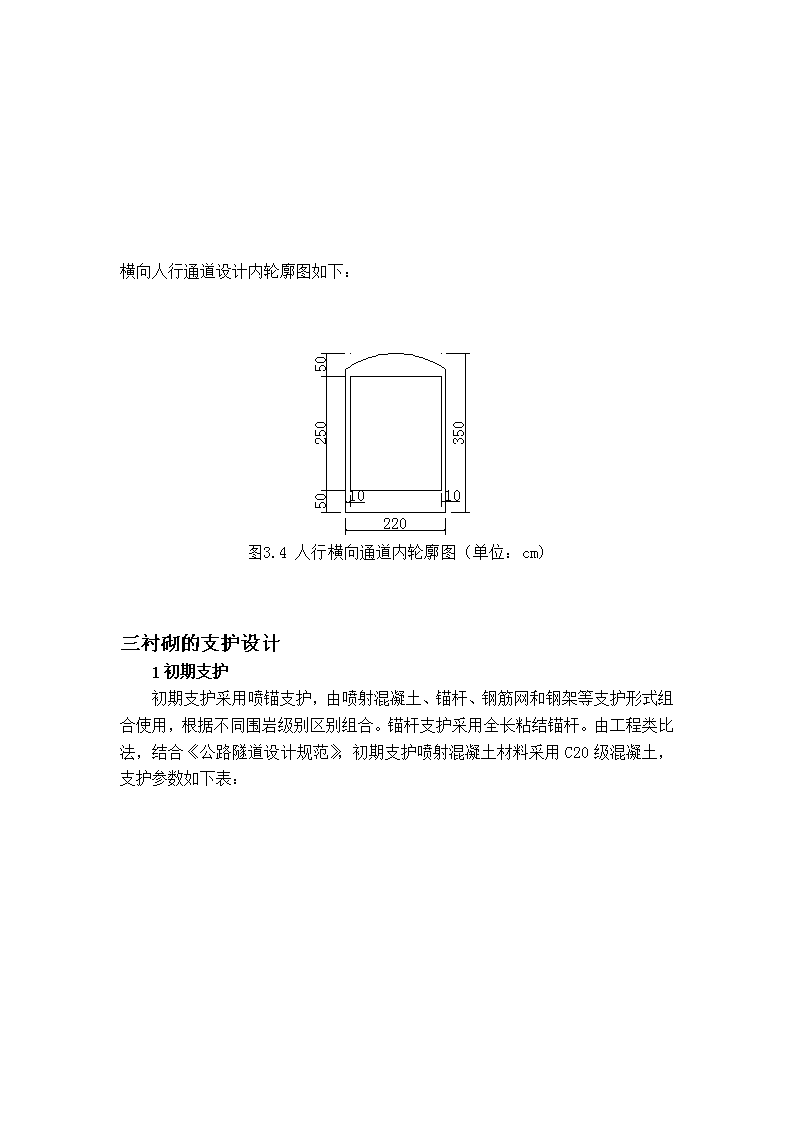
《隧道工程》课程设计任务书一基本资料1、工程概况：大云隧道位于某低山丘陵区。设计行车速度：80km/h2、地形地质条件施工地段属亚热带湿润季风气候区，属于剥蚀山丘地区，年均降雨量约1300mm。3、设计标准设计等级：高速公路单向二车道；地震设防烈度：6级二内轮廓的设计1根据设计资料：设计等级：高速公路单向二车道，由《公路隧道设计规范》（JTGD70-2004）4.3.2有：高速公路、一级公路的隧道应设计为上、下行分离的独立双洞。对于Ⅲ级围岩，容重=23.5KN/m3，围岩的弹性抗力系数K=1000MPa;分离式独立双洞间的最小净距为2.0B，B为隧道开挖断面的宽度。得出各断面内轮廊如下图： 横向人行通道设计内轮廓图如下：三衬砌的支护设计1初期支护初期支护采用喷锚支护，由喷射混凝土、锚杆、钢筋网和钢架等支护形式组合使用，根据不同围岩级别区别组合。锚杆支护采用全长粘结锚杆。由工程类比法，结合《公路隧道设计规范》，初期支护喷射混凝土材料采用C20级混凝土，支护参数如下表： 2二次衬砌二次衬砌采用现浇模筑混凝土，利用荷载结构法进行衬砌内力计算和验算。二次衬砌厚度设置如下表：注：钢筋面积为纵向每1m的钢筋面积。四围岩压力的计算1计算断面参数确定隧道高度h=内轮廓线高度+衬砌厚度+预留变形量隧道跨度b=内轮廓线宽度+衬砌厚度+预留变形量2荷载确定（一）根据围岩压力计算公式：计算围岩竖向均布压力： 式中：s——围岩类别，此处s=4；——围岩容重，此处=23.5KN/m3；——跨度影响系数毛洞跨度=10.86+20.5+20.065=11.99m其中0.065m为一侧平均超挖量=11.99>5m，=0.1，此处=1+0.1（11.99-5）=1.699。所以有：此处超挖回填层忽略不计。(二)围岩水平均布压力：e=0.12q=0.12×71.868=8.624KPa3衬砌的几何要素 5衬砌几何尺寸内轮廓线半径=5.43m，。内径、所画曲线的终点截面与竖直轴的夹角，，；拱顶截面厚度：墙底截面厚度：因为此处因为断面尺寸不变，所以外轮廓断面尺寸可以直接计算出来。外轮廓线半径：拱轴线半径： 拱轴线各段圆弧中心角：6半拱轴线长度及分段轴长分段轴线长度：半轴线长度为：将半拱轴线等分为8段，每段长度：8各分块接缝（截面）中心几何要素（1）与竖直轴夹角另一方面，角度闭合差：（注：因墙底面水平，计算衬砌内力时用）（2）接缝中心点坐标计 当然，也可以在附图2上直接量出、。以后计算中只取四位小数。五计算位移1、单位位移用辛普生法近似计算。按计算列表进行。单位位移的计算见表4.1。（说明本设计计算一律保留四位小数，表格采用保留三位有效数字）表4.1单位位移计算表截面asin(a)cos(a)xydI1/Iy/Iy2/I(1+y)2/I系数1/300.0000.0001.0000.0000.0000.50.01960.0000.00096.0001113.8800.2400.9711.3630.1660.50.019615.9172.639130.4734227.7590.4660.8852.6460.6540.50.019662.75541.023262.5332341.6390.6640.7473.7741.4350.50.0196137.770197.713569.2524455.5190.8240.5664.6822.4640.50.0196236.573582.9861152.1322569.3990.9360.3525.3173.6810.50.0196353.4141301.0602103.8894 683.2780.9930.1175.6415.0150.50.0196481.4592414.6143473.5332794.9700.996-0.0875.6506.3890.50.0196613.3153918.2875240.9174890.0001.0000.0005.4167.7430.50.0196743.3285755.5897338.2451Σ7682262.18911170.54416462.921单位位移值计算如下计算精度校核为：闭合差：2、载位移——主动荷载在基本结构中引起的位移（1）每一楔块上的作用力竖向力：式中：——衬砌外缘相邻两截面之间的水平投影长度，又附图2量得：水平压力：式中：——衬砌外缘相邻两截面之间的竖直投影长度，由附图2量得：自重力：式中：——接缝的衬砌截面厚度 注：计算时，应该第8个楔块的面积乘以。作用在各楔块上的力均列入表4.2，各集中力均通过相应图形的形心截面集中力力臂Q(KN)G(KN)E(KN)aqagae00.0000.0000.0000.0000.0000.0001102.23215.8161.4930.6510.6800.346296.26015.8164.3920.5530.6270.471384.66815.8167.0350.4230.5410.595468.13815.8169.2670.2680.4220.679547.62015.81610.9580.0970.2790.723624.32015.81612.007-0.0790.1200.72572.93215.81612.286-0.260-0.0310.69180.00015.81612.0370.000-0.1450.671（2）外荷载在基本结构中产生的内力楔块上各集中力对下一接缝的力臂由图4.1中量得，分别记为、、。内力图按下式计算。弯矩：轴力：式中：、——相邻两接缝中心点的坐标增值，按下式计算：（4.9）的计算见下表4.3。表4.3载位移计算表截面-Qaq-Gag-EaeΣ(i-1)(Q+G)ΣE(i-1)△x△y-△xΣ(Q+G)-△yΣEMp000.0000.0000.000000.0000.0000.0000.0000.0001001.3600.0000.000-77.822 -66.553-10.752-0.5170.1662-53.232-9.912-2.069118.0481.4931.2830.488-151.456-0.729-295.2183-35.815-8.549-4.186230.1245.8851.1290.781-259.810-4.596-608.1744-18.261-6.677-6.292330.60812.920.9081.029-300.192-13.295-952.8915-4.619-4.413-7.923414.56222.1870.6351.217-263.247-27.002-1260.09461.921-1.901-8.705477.99833.1450.3241.334-154.871-44.215-1467.86670.7620.486-8.490518.13445.1520.0081.374-4.145-62.039-1541.29180.0002.298-8.077536.88257.438-0.2341.354125.630-77.771-1499.210表4.4载位移计算表截面sinacosaΣ(Q+G)ΣEsinaΣ(Q+G)cosaΣENP00100000.00000.240.971118.0481.49328.3321.45026.8820.240.4660.885230.1245.885107.2385.208102.0300.4660.6640.747330.60812.92219.5249.651209.8720.6640.8240.566414.56222.187341.59912.558329.0410.8240.9360.352477.99833.145447.40611.667435.7390.9360.9930.117518.13445.152514.5075.283509.2240.9930.996-0.087536.88257.438534.734-4.997539.7320.99610552.69869.475552.6980.000552.6981基本结构中，主动荷载产生弯矩的校核为：1045.835kN/m-8.624/2×7.98562=-274.975kN/m -179.1953kN/m另外，由上可知，因此得出闭合差（3）主动荷载位移计算过程见表4.5。表4.5主动荷载位移计算表截面MP01/Iy/I(1+y)MP0/IMp0y/IMP0(1+y)/I系数1/30.000960.0001.0000.0000.0000.0001.0000.000-77.8229615.9171.166-7470.875-1238.687-8711.0404.000-77.822-295.2189662.7551.654-28340.946-18526.418-46875.9252.000-295.218-608.17496137.7702.435-58384.681-83788.099-142166.6984.000-608.174-952.89196236.5733.464-91477.515-225428.231-316878.1122.000-952.891-1260.09496353.4144.681-120969.024-445334.862-566256.0034.000-1260.094-1467.86696481.4596.015-140915.096-706717.095-847604.3012.000-1467.866-1541.29196613.3157.389-147963.917-945296.771-1093305.3864.000-1541.291-1499.21096743.3288.743-143924.189-1114404.992-1258329.1811.000-1499.210　　　Σ-668181.764-2972794.052-3640934.122　　 主动荷载位移：-3544.245×10-6-1.3753/(2.6×10-6)×2972794.052=-157249.372×10-6-192591.412×10-610-6闭合差3、载位移——单位弹性抗力及相应的摩擦力引起的位移（1）各接缝处的抗力强度抗力上零点假定在接缝3与4的中线处，最大抗力值假定在接缝5与6的中线处，最大抗力值以上各截面抗力强度按下式计算：查表4-1，算得：最大抗力值以下各截面抗力强度按下式计算：(4.14)式中：——所考察截面外缘点到点的垂直距离；——墙脚外缘点到点的垂直距离。由图4-1中量得： 则按比例将所求得的抗力绘于图4-1上。（2）各楔块上抗力集中力按下式近似计算：(4.15)式中：——楔块外缘长度，可通过量取夹角，用弧长公式求得，的方向垂直于衬砌外缘，并通过楔块上抗力圆形的形心。（3）抗力集中力与摩擦力的合力按下式计算：(4.16)式中：——围岩与衬砌间的摩擦系数，此处取。则：(4.17)其作用方向与抗力集中力的夹角。由于摩擦阻力的方向与衬砌位移的方向相反，其方向向上。画图时，也可取切向：径向=1：5的比例求出合力的方向。的作用点即为与衬砌外缘的交点。将的方向线延长，使之交于竖直轴，量取夹角，将分解为水平与竖直两个分力：{(4.18)以上计算列入表4.6。表4.6弹性抗力及摩擦力计算表截面σ（σnσ（σn)0.5(σi-1+σi)(σn)△S外R(σn)ψk?7sinψkcosψkRH(σn)RV(σn)30.0000.0000.0000.0000.0000.0000.0000.0000.00040.3260.1630.7180.11964.5570.9030.4300.1080.05150.8240.5751.4370.84374.7960.9650.2620.8130.221 60.9610.9461.4371.38687.8170.9990.0381.3850.05370.6360.7991.4271.162101.0410.981-0.1921.141-0.22380.0000.3181.4180.460109.4270.943-0.3330.434-0.153（4）计算单位抗力及其相应的摩擦力在基本结构中产生的内力弯矩：(4.19)轴力：(4.20)式中：——力至接缝中心点的力臂，由图4.1量得。计算见下表4.7。表4.7计算表截面R4=0.1193σhR5=0.8426σhR6=1.3863σhR7=1.1621σhR8=0.4600σhMσ0(σh)r4iR4r4i(σh)r5iR5r5i(σh)r6iR6r6i(σh)r7iR7r7i(σh)r8iR8r8i(σh)40.2330.028-0.02851.6460.1960.6330.533-0.72962.9880.3562.0041.6890.7130.989-3.03474.2290.5043.3322.8082.0872.8930.7770.902-7.10885.3470.6384.5783.8573.4314.7562.1512.4990.9690.446-12.196计算见下表4.8。表4.8计算表截面asinacosaΣRV(σh)sinaΣRV(σh)ΣRH(σh)cosaΣRH(σh)Nσ0(σh)455.5190.8240.5660.0510.0420.1080.061-0.019 569.3990.9360.3520.2720.2550.9210.324-0.069683.2780.9930.1170.3250.3232.3060.2700.053794.9700.996-0.0870.1030.1023.447-0.2990.401890.0001.0000.000-0.050-0.0503.8810.000-0.050（5）单位抗力及相应摩擦力产生的载位移计算见表4.9。表4.9单位抗力及摩擦力产生的载位移计算表截面Mσ0(σh)1/Iy/I(1+y)Mσ0/IMσ0y/IMσ(1+y)/I系数1/34-0.02896236.5733.464-2.665-6.568-9.23325-0.72996353.4144.681-70.011-257.737-327.74746-3.03496481.4596.015-291.295-1460.904-1752.20027-7.10896613.3157.389-682.372-4359.469-5041.84148-12.19696743.3288.743-1170.824-9065.692-10236.5161　　　　Σ-1589.425-10156.486-11745.911　校核为：闭合差4、墙底（弹性地基上的刚性梁）位移单位弯矩作用下的转角：单位弯矩作用下的转角：主动荷载作用下的转角：单位抗力及相应摩擦力作用下的转角： 5、解力法方程衬砌矢高计算力法方程的系数为：以上将单位抗力产生的位移乘以即为弹性抗力引起的位移。求解方程：显然可知： ，可将上述结果代入原方程，进行校核。6、计算主动荷载和被动荷载（）分别产生的衬砌内力计算公式：{(4.28){(4.29)计算过程列表4.10与表4.11。表4.10主、被动荷载作用下衬砌弯矩计算表截面MPOX1PX2P*y[MP]Mσ0(σh)X1σ(σh)X2σ*y(σh)[Mσ](σh)00.000329.4070.000329.4070.000-2.6360.000-2.6361-77.822329.40725.827277.4120.000-2.6360.311-2.3252-295.218329.407101.751135.9400.000-2.6361.224-1.4123-608.174329.407223.262-55.5050.000-2.6362.6850.0494-952.891329.407383.357-240.127-0.028-2.6364.6101.9465-1260.094329.407572.701-357.986-0.729-2.6366.8873.5226-1467.866329.407780.249-358.210-3.034-2.6369.3833.7137-1541.291329.407994.020-217.864-7.108-2.63611.9542.2108-1499.210329.4071204.67934.876-12.196-2.63614.487-0.345表4.11主、被动荷载作用下衬砌轴力计算表截面NP0X2Pcosa[NP]Nσ0(σh)X2σcosaNσ(σh)00.000155.583155.58301.8711.871 126.882151.071177.95301.8171.8172102.030137.691239.72101.6561.6563209.872116.221326.09301.3981.3984329.04188.060417.101-0.0191.0591.0405435.73954.765490.504-0.0690.6590.5906509.22418.203527.4270.0530.2190.2727539.732-13.536526.1960.401-0.1630.2388552.6980.000552.698-0.050.000-0.0507、最大抗力值的求解首先求出最大抗力方向内的位移。考虑到接缝5的径向位移与水平方向有一定的偏移，因此修正后有：{(4.30)(4.32)表4.12最大抗力位移修正计算表截面MP/IMσ/I(σh)(y5-yi)MP(y5-yi)/IMσ(y5-yi)/I系数1/3031623.072-253.0563.681116404.528-931.4991126631.568-223.2403.51693636.594-784.9114213050.249-135.5873.02839516.153-410.55823-5328.4954.6932.246-11967.80010.54044-23052.218186.8301.217-28054.549227.37225-34366.654338.12600.0000.0004　　　Σ155334.304-1465.118　把计算过程列入表4.12，位移值为最大抗力值为： 8、计算衬砌总内力按下式计算衬砌总内力：{(4.34)计算过程列入表4.13表4.13衬砌总内力计算表截面MPMσ[M]NPNσ[N]eM/IMy/I系数1/30329.407-2.63653.734155.5831.871351.2520.0875158.4760.00011277.412-2.32534.220177.9531.817367.9480.0933285.156545.33642135.940-1.412-11.765239.7211.656412.888-0.028-1129.454-728.49823-55.5050.049-50.393326.0931.398472.258-0.089-4837.705-6942.10744-240.1271.946-36.600417.1011.040525.863-0.070-3513.555-6867.39925-357.9863.52210.361490.5040.590552.1640.019994.6153598.51646-358.2103.71330.103527.4270.272555.8640.0542889.84014492.54827-217.8642.21013.239526.1960.238551.1090.0241270.9308119.9704834.876-0.345-0.845552.698-0.050547.469-0.002-81.120-628.1121　　　　　　　Σ1474.33311484.017　计算精度的校核为以下内容。根据拱顶切开点的相对转角和相对水平位移应为零的条件来检查：式中：相对误差可按此式计算。 相对误差可按此式计算。显然闭合差满足要求。9、衬砌截面强度检算检算几个控制截面：1、拱顶（截面0）（可满足要求），可得：（可）式中：-混凝土极限抗压强度，取2截面1（可满足要求），可得：（可）式中：-混凝土极限抗压强度，取3截面5（可满足要求），可得： （可）式中：-混凝土极限抗压强度，取4截面8满足要求其它各截面偏心均小于0.45d。综上，验算满足强度要求。3.3.1配筋计算经过计算，可知中墙顶部为最不利位置，沿隧道纵向取1m的计算单元，弯矩最大为53.734kN.m，轴力为351.252kN，以此截面为控制截面进行配筋，为简便计算，可以对称配筋。弯矩设计值，轴力设计值截面长度：L=1.0m高度：计算长度：偏心距：附加偏心矩：（20mm和1/30偏心方向截面尺寸中较大值）初始偏心矩：=20+153=173mm偏心距增大系数：，所以取所以构件长细比对截面曲率影响的系则偏心矩增大系数： 1.268×153>0.3×450按大偏心受压构件进行计算153×1.268+500/2－50=394mm取则受压区钢筋面积：采用20Φ20，=6248，非超筋，满足要求。