最新天津大学船舶与海洋工程8结构力学课件第二课件1教学课件

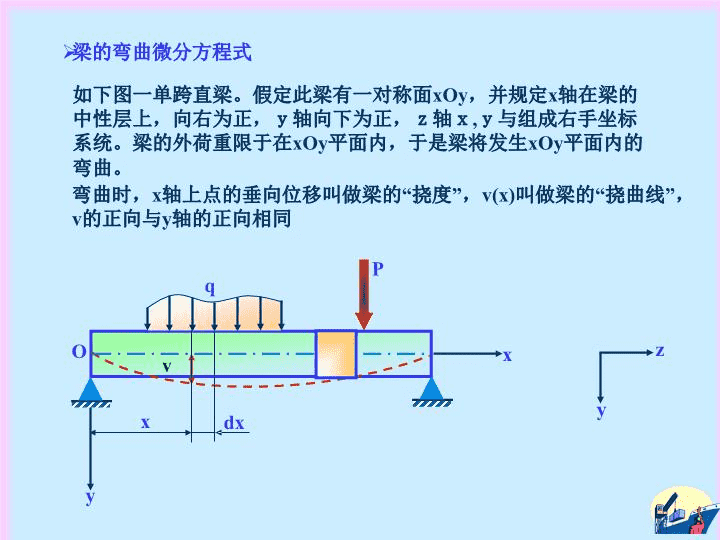
天津大学船舶与海洋工程8结构力学课件第二课件1 §2-1梁的弯曲微分方程式及其积分基本概念：梁：单跨梁：基本假设：平断面假设。（在纯弯曲条件下严格满足）符号法则：梁的挠度v——向下为正。梁的断面转角dv/dx——顺时针方向为正。梁断面的弯矩M——在左断面逆时针方向为正，右断面顺时方向为正。梁端面的剪力N——在左断面向下为正，在右断面向上为正。本节寻求梁挠度曲线方程式的基本方法：初参数法仅在两端有支座支持的梁，称之为“单跨梁”。受横向外载荷作用而发生弯曲变形的杆件。 分析Oblxy q(x)POblxyacxd现应用这个概念于在跨度中受集中力作用的梁。m POxbcyad综上所述，如图对于一般荷重作用下的挠曲线方程式可表示如下：q(x)m由 §2-2梁的支座及边界条件自由支持在刚性支座上如图：刚性固定在刚性支座上如图: RR弹性支座vvAA左端断面：右端断面：弹性支座边界条件为：自由支持在弹性支座上的边界条件为：刚性固定在弹性支座上的边界条件为： 弹性固定端MM等价于节点受到的力梁受到的力大小相等方向相反MM柔度系数：单位弯矩引起的转动角度。刚度系数：单位位移引起的力矩 左端断面：右端断面：弹性固定端边界条件为：梁端弹性固定在刚性支座上：弹性固定在弹性支座上：如果，表示是完全自由端 qOylx例1如图，求两端自由支持在刚性支座上，受均布荷重作用的梁的挠曲线解：边界条件：该题特点：静定结构，可直接得到节点上的约束反力： 讨论：本梁约束的特点、位移的特点、内力分布的特点若梁两端为自由支持在弹性支座的边界，挠曲线及内力分布如何？若改变梁两端弹性支座的刚度系数或柔度系数，挠曲线及内力分布如何？ PAxy例2如图，求受集中力作用的单跨梁的挠曲线方程式。梁的左端为弹性固定端，柔性系数为；梁的右端为弹性支座，柔性系数为解：x=0处的边界条件为:x=l处的边界条件为:=0 讨论：梁为超静定结构，弹性固定端及弹性支座的柔度系数变化对位移及梁内力分布会产生什么影响？ xyl例3如图，两端刚性固定的梁，不受外荷重，当其由支座发生位移时，求其挠曲线与断面弯矩与剪力。因左端为刚性固定，故所以：当x=L时，故 解得：挠曲线方程式为：梁两端剪力均为：梁两端弯矩均为：讨论弯矩图与剪力图的分布特点 §2-3梁的弯曲要素表及应力计算单跨梁的弯曲要素表由于目前梁的弯曲公式是在小变形与材料符合胡克定律的前提下导得的，所以梁的弯曲要素与梁上的外载荷成正比，或梁的弯曲要素与外力成线性关系。这样，如果梁上受到几种不同的外力作用时，就可以用“叠加原理”（Principleofsuperposition)来进行计算。PvM例1如图，求梁中点挠度、端点转角并画出梁的弯矩图、剪力图。梁上所受的外力为集中外弯矩m及集中力P,并已知m=0.2Pl。解：将此梁分为一个仅受外弯矩m的梁及一个仅受集中力P的梁，叠加起来得： Pvmv1v2m0.15Pl0.2Pl0.2Pl0.25Pl0.7P0.3P0.2P0.5P0.5PP Q例2如图，计算一端刚性固定另一端自由支持梁的中点挠度，右端转角并画出梁的弯矩、剪力图。解：PPQM PQPQM弯矩图剪力图 m例3计算如图两端刚性固定梁的弯曲要素解：mM1M2 AP例4计算如图一端弹性固定，另一端弹性支座梁的中点挠度、端点转角并画出弯矩、剪力图。v1Pm已知解：先求出弹性固定段弯矩：梁化为： v1APPm 梁的应力断面距中性轴y处的正应力为如下图梁的剪应力产生的原因矩形断面：式中： 圆断面：矩形断面：的薄壁断面：(a)剪流(b)S图从而中性轴处剪应力最大：yyzzs (a)剪流(b)S图工字形断面最大剪应力为：具有对称轴的闭口薄壁盒形断面Aw为腹板面积 结束语谢谢大家聆听！！！32