最新天津大学船舶与海洋工程8结构力学课件第九放映教学课件

天津大学船舶与海洋工程8结构力学课件第九放映 §9-1概述本章主要讨论的对象为承受各种垂直于板面载荷的、具有不同边界条件的矩形平板弯曲时的应力与变形问题；板为四周支持在纵骨架上的矩形平板；通常不考虑连续板；船体结构中的板属于薄板的范畴，其厚度t与板短边b比值在以下范围内： 板面的最大正应力：板条梁断面的弯曲正应力沿断面高度线性分布位于板的上下表面 yxqlTT筒形板的复杂弯曲（a）此时，板除受横载荷外，还在长边受到中面应力，据前分析可得：其中求得板条梁的断面弯矩，可求得总应力如图： 例设有一两端自由支持的板条梁，,受均布荷重，并有中面应力，计算此板条梁的最大应力。材料的弹性模数解：先假设中面力为拉力，计算参数u:故板条梁中点的最大弯矩为最大弯曲应力为：最大总应力为：如果此板不受中面力，则最大弯矩为：最大弯曲应力为：板条梁筒形刚度：中点挠度：此值已大大超过一般钢材的屈服极限，此板没有中面拉力不能承受横载荷。亦不能承受中面拉力 此例说明：中面拉力对板的承载其了很大的作用：如果没有中面力，板在横荷重下会发生很大的应力与应变;板似乎不能承受中面压力。但对于船体板后两结论不正确，由于实际船体板的支持骨架相当强，板在弯曲时其支持骨架总是阻止板边（板条梁）的两端自由趋近，因此板本身就会因弯曲而拉长，从而发生中面拉伸力。这种中面力不容忽视，否则会低估办得承载能力。因此我们将在下节研究办的大挠度弯曲问题. qxdxdxdwxzdsl筒形板的大挠度弯曲为研究板弯曲时因支座阻碍板边趋近而产生的中面力，先考虑板边完全不可趋紧的情况。在板条梁中取出一长度为地dx微段他在变形后的长度为ds，如图：微段变形后长为：整个板条梁伸长为（9-14）所以： 板条长度方向的应变为：将（9-14）代入：上式联系了板条梁中面力T与挠度w之间的关系，但若要求出T还要利用板条梁的复杂弯曲微分方程式。（9-15）①将（9-15）式中的T代入复杂弯曲微分方程式的解中求出挠曲线；实际上我们可利用复杂弯曲梁的解的方式获得。（查表、初参数方法）两个未知数两个方程完全可以求解具体方法是：②再把求的W(x,y)代回（9-15）,销去W，解出T。 (1)板条梁两端自由支持受均布荷重：①求出挠曲线将w带入（9-16）（9-17）举例：由§2-5（2-64），将其中EI用D代换得：得：该方程为超非线性方程，无法直接解方程，可采用数值解法。 （2）板条梁两端刚性固定受均布荷重：同样由第二章公式：代入（9-15)式中，可得：由所得公式（9-17）及（9-19），当板的尺寸，材料及荷重已知时可解出u,从而得板的中面力为为了实际应用，已将公式（9-17）及（9-19）的关系画成曲线（见下页），并令（9-18）（9-19）（9-20）（9-21） C1.31.21.11.00.90.80.71.31.21.11.00.90.80.72.22.12.01.91.81.51.71.61.41.31.24.03.53.02.52.02.01.51.03.02.52.00.90.93.50123489101112456780123445678(b)板条梁两端自由支持板条梁两端刚性固定ABCCBA曲线A-u由0到4曲线B-u由4到8曲线C-u由8到12(a) 例设有一两端自由支持的板条梁，,受均布荷重，计算此板条梁的最大应力。材料的弹性模数。解：先按公式（9-21）算出U：查图(a)得u=2.60，故：当u=2.60时，由附录B，得板条梁中点最大挠度与弯矩分别为板最大弯曲应力为：最大总应力为：考虑了板自身弯曲而产生的中面力影响后，此板可承受的外载荷重，，，，，结论 由公式（9-21）及图（a),(b)知当板的柔性大且外力大时：U就小，这时u就小，表明中面拉力T大；反之，如板的柔性小且外力小：则U大，u小，表明中面拉力小 据此，在板的弯曲问题中长把板分为以下几类：（1）刚性板——中面力对弯曲要素可以忽略不计的板；（2）柔性板——中面力对弯曲要素不可略不计的板；（3）薄膜——板的中面力远较弯曲力为大，板主要靠中面拉力承载。以上推导是在板边完全不能靠近时得到的，但实际的板条梁两端不会绝对不能趋近，亦不会完全可以自由趋近。因此实际中的中面拉力比以上的结果要小。反映在公式中，将（9-17）菏（9-19）等号左边乘一个影响系数：当时，中面应力对板条梁弯曲要素的影响可以忽略不计由得，，最终推得：表明当板条梁受载荷时的最大挠度小与板厚的1/5时，可不计弯曲产生的中面力。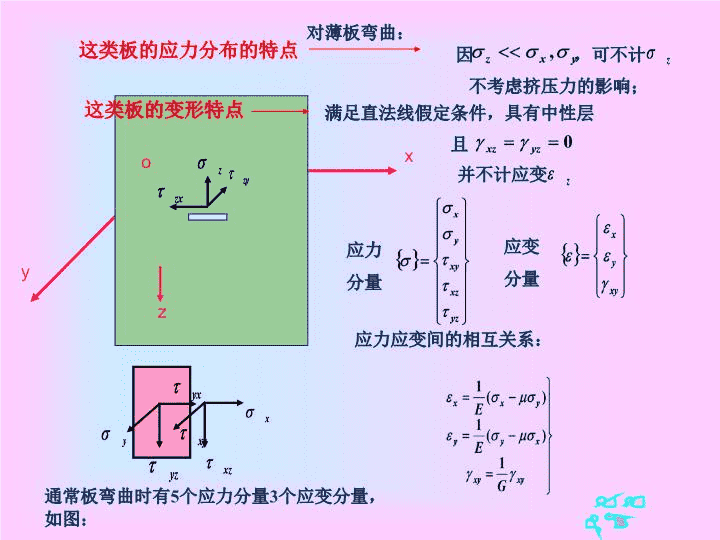对两端刚性固定的情况亦可导得类似的结论：（9-22） §9-3刚性板的弯曲微分方程式本节开始研究矩形板的一般弯曲，板只有横载荷，没有中面载荷，亦不考虑板变形而产生的中面。如图:建立坐标系yoxztab基本假定：直法线假定据此板z方向的正应力与其他应力相比可忽略不计不计板中面的变形 1、根据变形的假定条件及几何关系式求出应变与挠度w之间的相互关系；2、根据物理方程与挠度w之间的相互关系；3、一dxdy微块上断面的合力及合力矩，与挠度w之间的相互关系；4、微块上力的平衡条件得到进而得到外力q(xy)与挠度之间的关系。即弯曲板微分方程式求解刚性板弯矩微分方程的基本过程 zox弯曲微分方程式刚性板的弯曲微分方程式可以用梁的弯曲微分方程式相同方式建立：（1）应变与位移间的关系：取微块dxdy,如图因此：同理：（9-24）（9-23）目的：通过几何变形分析找出应变与挠度之间的关系剪应变的求解思路：通过上两式求出位移u（x，y）、v（x，y）根据求出 同理板剪应变为：（9-26）根据刚性板弯曲中性面不发生面内位移及变形的假定：带入上式得： 弯曲时应变与位移间的关系，可用矩阵写为：或式中： （2）应力与应变间关系：应用方程式（9-2)得：将（9-28）代入上式，得分析应力分布的特点：沿板厚线性分布，在中性层处应力为零 （3）板单位宽度断面上的力和力矩：板中取一微块，微块断面上分别有应力，及 板边dx上单位宽度上断面上力和力矩由剪力互等定理得：板边dy上单位宽度上断面上力和力矩其中通过力的平衡条件求得。 将应力代入得：式中为板的刚度矩阵，所以上式可表达为： 式中：[D]为薄板弯曲问题中的“弹性矩阵” （4）静力平衡条件建立板中面微块的平衡方程式，使所有力对Oy轴的合力矩为零，得：如图： 从上式可以看到，在列平衡是不能忽略，因为它们直接构成域外荷重相平衡略去三阶微量，并同除以dxdy得： 所有的力在Oz轴上的投影力为0，得：此处表示算子刚性板一般弯曲的平衡微分方程式，也可写成： 这样，一旦求得板的挠曲函数w(x,y),得板弯曲时的应力为上式可简写为求解w是关键：边界条件的引入 边界条件刚性板一般弯曲的微分方程式是两个变数的四阶线性偏微分方程式。解时要有八个任意常数。因此必须有八个边界条件。看一下四种情况：板自由支持在刚性周界上（如图）：板刚性固定在刚性周界上（如图）：此时板边缘挠度和弯矩均为零，因此在x=0和x=a处有因边缘处板没有挠度，所以从而：同理： ybzox在dx范围内所有的剪力单位宽度上的合成力=向下为正b在中间dx上的扭矩的等效合力弹性支座边（弹性支座支持在刚性支座上）： ybzox单位长度上等效合力在边缘y=b处有：弹性支座边（弹性支座支持在刚性支座上）：在边缘x=a处有：在边缘y=0处有：单位长度上等效合力 ybzoxb一边为自由支持在刚性周边或弹性周边上时，边的两角会出现集中力四边均为自由支持在刚性周边或弹性周边上时，四角会出现集中力 板的边缘为自由边：若y=b边为自由边，则该边应满足：这样有三个边界条件，但在解弯曲微分时，只允许有两个边界条件，因此，把剪力与扭矩都为零的条件化为等效剪力为零的条件：ybzox若x=a边也为自由边，则该边应满足：x=a，y=b角点处应满足： §9-4刚性板弯曲的解满足两个基本条件条件应用双三角级数解四边自由支持板的弯曲对于四周自由支持的板，板的挠曲线在支持周边上必须适合下列条件为求解微分方程式（9-43），将w(x,y)写成下面的形式（9-51）（9-52）yx将该函数带入力的平衡条件求解可见该函数自然满足边界条件 （9-53）（9-54）将外载荷用三角级数展开：其中： （1）若板上有均布载荷,这样： (2)若板受集中力P,作用点坐标为，如图：oyxab在集中力作用处，取边长为的矩形微块，并认为此微块作用着强度为：分布荷重。用公式（9-58），得：当趋于零时，其极限为于是：说明当P作用在处，则在板任意点（x,y)处引起的挠度就等于P作用在板上任意点(x,y)处在处所产生的挠度，这就是位移互等定理。应用双三角级数对板弯曲问题的解称为“纳维叶解”。P yx应力单三角级数解一对边自由支持的弯曲一对边(x=0,x=a的边)为自由支持，另一对边为任意固定的板可将弯曲微分程式的解取单三角级数形式：为y的任意函数此时设定的函数自然满足x边的边界条件，计算求解需利用力的平衡条件及y的边界条件满足x=0,x=a的边界条件其中： 把荷重q(x,y)展开成相应的单三角函数：式中：得：求解上式的通解和它的特解组成。（9-66）解：（1）代入弯曲微分方程式得：（2）利用公式特点是y的单值函数 通解可将代入方程（9-66）得特征方程式：求解上式的通解和它的特解组成。通解齐次方程：（3）特解方程依具体外载形式而定本解特点（1）y的单值函数；（2）4个待定参数。 此特征方程式有成对的重根：于是齐次方程的通解可以写成下面的形式：或用双曲线函数表示成：从而微分方程式（9-65）的一般解为：式中为特解（9-67）（9-68）（9-69） oxya例试决定自由支持在边缘x=0与x=a处及刚性固定在边缘y=+b/2的挠曲线（如图）。板上受均布荷重q0解：由于板的挠曲面对称于OX轴，因而函数中的奇函数项的系数应等于零，及于是其中特解可以这样求得。因为（9-70） 积分常数可以由处的边界条件来决定。所以从此方程中看到，只要取特解为常数就能成为方程的解当时，即：将式（9-70）代入此边界条件得： 式中。由此解得：将求得之常数代入(9-70),得：于是板挠曲函数为：（9-71） ayobx四边刚性固定的板的解如图：板中点挠度板中点，与短边平行的断面（垂直于x轴的断面）中的弯矩：板中点，与长边平行的断面（垂直于y轴的断面）中的弯矩：板短边中点的弯矩：板短边中点的弯矩：以上公式中的系数k1、k2、k3、k4及k随板的边长变化，见下页(a)图。有板上下表面的弯曲正应力的按下式计算：由(a)图可知k5最大，因此板总是在长边中点的弯矩最大，因此该处应力以最大。当a/b相当大时，k5=0.0833,由此得长边中点断面的最大弯曲应力为：（9-72）（9-73）（9-74）（9-75）（9-76）（9-77） 由(a)图可知k5最大，因此板总是在长边中点的弯矩最大，因此该处应力以最大。当a/b相当大时，k5=0.0833,由此得长边中点断面的最大弯曲应力为：2.82.41.80.080.070.060.050.040.030.020.011.00.091.21.42.21.62.02.63.0k5k4k3k1k2以上公式中的系数k1、k2、k3、k4及k随板的边长变化，见图。板上下表面的弯曲正应力的按下式计算： oyxs(b)纵骨架式船体板（a>b)，当边长比相当大时，取k2=0.0125,k4=0.0571,分别得沿船长方向跨度中点和支座断面中的应力（9-77）为：横骨架式船体板（如图），设短边长度为s,当边长比相当大时，取k3=0.0417,k5=0.0833,分别得沿船长方向跨度中点和支座断面中的应力为：从此例题获得的结论： 习题1矩形水平薄板OABC的OA边和OC边为简支边，AB边和CB为自由边,在B点上受集中铅直力P作用。试证w=mxy满足一切条件，并求出挠度、弯矩和角点反力。xyoABCabP习题2xyoABCab简支边受到均布弯矩M、两个自由边受到均布弯矩μM作用。试证:w=f(x,y)满足一切条件并求出挠度。MMμMμM习题32一椭圆形薄板，边界方程为试取挠度的表达式为其中m为任意常数，求挠度表达式。abxy 习题1解满足条件1）力的平衡条件2）边界条件①②③④⑤习题2解满足条件1）力的平衡条件2）边界条件①②③④求出参数后代入y=0及y=b的边界条件进行验证。 习题3解满足条件1）边界条件当时：①②2）力的平衡条件求得m 李兹法求解板弯曲问题势函数板弯曲应变能 对Z积分 格林函数积分：设C为域D的边界曲线，P（x,y）,Q(x,y),及其偏导数在简单闭域D以及边界上C单值连续，那么有公式： 矩形板四周支持在刚性支座上，板的四边的挠度等于0时，上式积分=0板弯曲应变能 结束语谢谢大家聆听！！！62