中南大学结构力学课件--5静定平面桁架.ppt

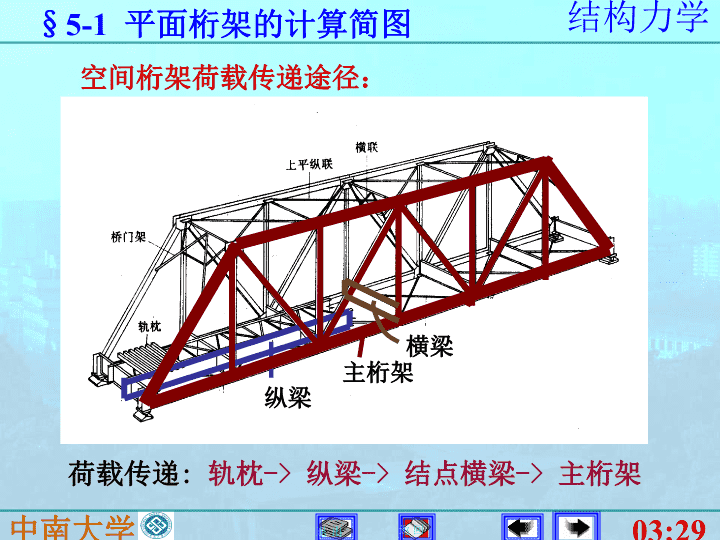
第五章静定平面桁架§5-1平面桁架的计算简图§5-2结点法§5-3截面法§5-4截面法与结点法的联合应用§5-5各式桁架比较§5-6组合结构的计算 桁架是由杆件相互连接组成的格构状体系，它的结点均为完全铰结的结点，它受力合理用料省，在建筑工程中得到广泛的应用。1、桁架的计算简图(trussstructure)武汉长江大桥所采用的桁架型式屋架计算简图§5-1平面桁架的计算简图 纵梁主桁架横梁空间桁架荷载传递途径：荷载传递:轨枕->纵梁->结点横梁->主桁架§5-1平面桁架的计算简图 上弦杆Topchard下弦杆Bottomchard竖杆Verticalchard斜杆Diagonalchard跨度桁高弦杆腹杆节间d经抽象简化后，杆轴交于一点，且“只受结点荷载作用的直杆、铰结体系”的工程结构—桁架桁架各部分名称：§5-1平面桁架的计算简图 桁架计算简图假定：(1)各杆在两端用绝对光滑而无摩擦的铰（理想铰）相互联结。(2)各杆的轴线都是直线,而且处在同一平面内，并且通过铰的几何中心。(3)荷载和支座反力都作用在结点上,其作用线都在桁架平面内。思考:实际桁架是否完全符合上述假定?主内力:按理想桁架算出的内力，各杆只有轴力。实际桁架不完全符合上述假定,但次内力的影响是次要的。§5-1平面桁架的计算简图次内力：实际桁架与理想桁架之间的差异引起的杆件弯曲，由此引起的内力。 2、桁架的分类一、根据维数分类1）.平面（二维）桁架（planetruss）——所有组成桁架的杆件以及荷载的作用线都在同一平面内§5-1平面桁架的计算简图 2）.空间（三维）桁架（spacetruss）——组成桁架的杆件不都在同一平面内§5-1平面桁架的计算简图 二、按外型分类1.平行弦桁架2.三角形桁架3.抛物线桁架§5-1平面桁架的计算简图 三、按几何组成分类2.联合桁架（combinedtruss）3.复杂桁架（complicatedtruss）§5-1平面桁架的计算简图1.简单桁架（simpletruss） 四、按受力特点分类2.拱式桁架竖向荷载下将产生水平反力1.梁式桁架§5-1平面桁架的计算简图 二、桁架的内力计算1.结点法和截面法结点法—最适用于计算简单桁架。取结点为隔离体，建立（汇交力系）平衡方程求解。原则上应使每一结点只有两根未知内力的杆件。通常假定未知的轴力为拉力，计算结果得负值表示轴力为压力。§5-2结点法 例5-1试用结点法求三角形桁架各杆轴力。解:(1)求支座反力。(↑)(↑)(2)依次截取结点A，G，E，C，画出受力图，由平衡条件求其未知轴力。§5-2结点法 取A点为隔离体，由（拉）所以（压）有§5-2结点法 取G点为隔离体§5-2结点法 取E点为隔离体，由联立解出，§5-2结点法 取C点为隔离体，由得，，§5-2结点法 可以看出，桁架在对称轴右边各杆的内力与左边是对称相等的。结论：对称结构，荷载也对称，则内力也是对称的。§5-2结点法 以结点作为平衡对象，结点承受汇交力系作用。按与“组成顺序相反”的原则，逐次建立各结点的平衡方程，则桁架各结点未知内力数目一定不超过独立平衡方程数。由结点平衡方程可求得桁架各杆内力。小结:§5-2结点法 1.对于一些特殊的结点，可以应用平衡条件直接判断该结点的某些杆件的内力为零。零杆(1)两杆交于一点，若结点无荷载，则两杆的内力都为零。§5-2结点法结点法计算简化的途径： (2)三杆交于一点，其中两杆共线，若结点无荷载，则第三杆是零杆，而在直线上的两杆内力大小相等，且性质相同（同为拉力或压力）。§5-2结点法 (3)四杆交于一点，其中两两共线，若结点无荷载，则在同一直线上的两杆内力大小相等，且性质相同。推论，若将其中一杆换成外力F，则与F在同一直线上的杆的内力大小为F，性质与F相同。§5-2结点法 (4)四杆交于一点，其中两两共线，若结点无荷载，则在同一直线上的两杆内力大小相等，且性质相同。§5-2结点法 值得注意：若事先把零杆剔出后再进行计算，可使计算大为简化。§5-2结点法FP/2FP/2FPFPFP 零杆:轴力为零的杆练习:试指出零杆受力分析时可以去掉零杆,是否说该杆在结构中是可有可无的?§5-2结点法 §5-2结点法练习:试指出零杆 §5-2结点法练习:试指出零杆 下图示对称结构在正对称荷载作用下，若A点无外荷载，则位于对称轴上的杆1、2都是零杆。练习:试指出零杆§5-2结点法为什么? FAyFBy结点法计算简化的途径：2.对称结构受对称荷载作用,内力和反力均为对称:受反对称荷载作用,内力和反力均为反对称。E点无荷载,红色杆不受力FAyFBy垂直对称轴的杆不受力对称轴处的杆不受力§5-2结点法 应用范围1、求指定杆件的内力；2、计算联合桁架。截面法定义:作一截面将桁架分成两部分，然后任取一部分为隔离体(隔离体包含一个以上的结点)，根据平衡条件来计算所截杆件的内力。联合桁架(联合杆件)指定杆件(如斜杆)§5-3截面法 截面法计算步骤2.作截面(用平截面，也可用曲截面)截断桁架，取隔离体；3.(1)选取矩心，列力矩平衡方程(力矩法)(2)列投影方程(投影法)；4.解方程。1.求反力(同静定梁)；注意事项1、尽量使所截断的杆件不超过三根(隔离体上未知力不超过三个)，可一次性求出全部内力；2、选择适宜的平衡方程，最好使每个方程中只包含一个未知力，避免求解联立方程。3、若所作截面截断了三根以上的杆件，但只要在被截各杆中，除一杆外，其余均汇交于一点(力矩法)或均平行(投影法)，则该杆内力仍可首先求得。分类力矩法和投影法§5-3截面法 示例1：试求图示桁架中杆EF、ED，CD，DG的内力。截面如何选择？§5-3截面法 解:(1)求出支座反力FA和FB。(2)求下弦杆CD内力，利用I-I截面，力矩法FAd-F1d-F2×0-FNCDh=0FNCD=(FAd-F1d-F2×0)/h与等代梁比较，得出：FNCD=M0E/h（自己总结）当荷载向下时，M0E为正，FNCD为拉力，即简支桁架下弦杆受拉。取EF和ED杆的交点E为矩心，CD杆内力臂为竖杆高h，由力矩平衡方程∑ME=0，可求CD杆内力。§5-3截面法 (3)求上弦杆EF内力FA×2d-F1×2d-F2d+FxEFH=0FxEF=-(FA×2d-F1×2d-F2d)/H与等代梁比较，得出：FxEF=-M0D/H，再由比例关系求FNEF。当荷载向下时，M0D为正，FNEF为压力，即简支桁架上弦杆受压。取ED和CD杆的交点D为矩心，由力矩平衡方程∑MD=0，先求EF杆的水平分力FxEF，此时力臂即为桁高H。§5-3截面法 (4)斜杆ED-FAa+F1a+F2(a+d)+FyED(a+2d)=0FyED=(FAa-F1a-F2(a+d))/(a+2d)再由比例关系求FNED，其拉或压需视上式右端分子为正或为负而定。取EF和CD杆的延长线交点O为矩心，并将FNED在D点分解为水平和竖向分力FxED和FyED，由力矩平衡方程∑MO=0，先求ED杆的竖向分力FyED，此时力臂即为a+2d。(5)DG杆如何求？利用II-II截面，投影法§5-3截面法 示例2：试求图示桁架a杆的内力。解(1)求支座反力。(2)直接求出a杆的位置困难。首先作截面Ⅰ-Ⅰ，求出FNEC，然后取结点E就可求出a杆的轴力。作截面Ⅰ-Ⅰ，取截面左侧部份为隔离体，由故§5-3截面法 (3)取结点E为隔离体，由思考：是否还有不同的途径可以求出FNα？§5-3截面法 截面单杆:用截面切开后，通过一个方程可求出内力的杆.截面上被切断的未知轴力的杆件只有三个,三杆均为单杆.截面上被切断的未知轴力的杆件除一个外交于一点,该杆为单杆.截面上被切断的未知轴力的杆件除一个均平行,该杆为单杆.截面法技巧：§5-3截面法 相交情况FPFPFPFPFPFPa为截面单杆§5-3截面法 平行情况FPFPb为截面单杆§5-3截面法 练习:求图示桁架指定杆件内力(只需指出所选截面即可)§5-3截面法 §5-3截面法 §5-3截面法 §5-3截面法 在桁架的计算中，结点法和截面法一般结合起来使用。尤其当（１）只求某几个杆力时；（２）联合桁架或复杂桁架的计算。例5-1试求图示K式桁架中a杆和b杆的内力。如何合理选择截面？杆件数大于3§5.4截面法与结点法的联合应用 截取结点K为隔离体，由K形结点的特性可知(结点法)FNa=-FNc或Fya=-Fyc由截面I-I(截面法)根据∑Fy=0有3F-F/2-F-F+Fya-Fyc=0即F/2+2Fya=0得Fya=-F/4由比例关系得FNa=-F/4×5/3=-F/12截面法不能直接求解§5.4截面法与结点法的联合应用 由截面I-I(截面法)根据∑MC=0即可求得FNb，FNb=-(3F×8-F/2×8-F×4)/6=-8F/3也可作截面II-II(曲截面)并取左半边为隔离体，(更简捷)由∑MD=0FNb×6+3F×8-F/2×8-F×4=0§5.4截面法与结点法的联合应用 例5-2试求图示桁架HC杆的内力。支座反力如图。取截面I-I以左为隔离体，由∑MF=0可得FNDE=90×5/4=112.5kN(拉)(截面法-力矩法)由结点E的平衡得FNEC=FNED=112.5kN(拉)§5.4截面法与结点法的联合应用 再取截面II-II以右为隔离体，由∑MG=0并将FNHC在C点分解为水平和竖向分力，可得FxHC=(30×15-112.5×6)/6=-37.5kN(拉)FyHC过铰G，不产生力矩，先求FxHC(截面法-力矩法)由几何关系FNHC=-40.4kN§5.4截面法与结点法的联合应用 对称结构:几何形状和支座对某轴对称的结构.对称荷载:作用在对称结构对称轴两侧,大小相等,方向和作用点对称的荷载反对称荷载:作用在对称结构对称轴两侧,大小相等,作用点对称,方向反对称的荷载对称荷载反对称荷载对称性的利用 对称结构的受力特点:在对称荷载作用下内力是对称的,在反对称荷载作用下内力是反对称的.对称平衡反对称平衡对称性的利用 例:试求图示桁架A支座反力.对称荷载反对称荷载000BC0对称性的利用 例:试求图示桁架各杆内力.对称性的利用 (a)例3:试对图(a)所示桁架，1)分析并确定求解整个桁架内力的路径；2)寻找只计算杆a轴力时的简捷方法，并求出杆a轴力§5.4截面法与结点法的联合应用(b)解：先求出支座反力，见图(b) (c)由图(c)所示截面左侧隔离体求出截面截断的三根杆的轴力后，即可依次按结点法求出所有杆的轴力。利用截面I—I截开两简单桁架的连接处，取截面任一侧为隔离体，见图(c)§5.4截面法与结点法的联合应用 见图(d)，由结点H的结点单杆EH上的轴力，再由结点E（当杆EH轴力已知时，杆a既是结点E上的结点单杆）可求出杆a的轴力。方法1：§5.4截面法与结点法的联合应用(d) 取截面II—II下为隔离体，见图(e)(e)方法2：§5.4截面法与结点法的联合应用该隔离体上有5根被截断的杆件，但有4根是交于一点A的，因此利用以铰A为矩心的力矩方程，可直接求出杆a的轴力。 将杆a轴力在B点分解，由§5.4截面法与结点法的联合应用 (a)例4§5.4截面法与结点法的联合应用解：由上部结构的整体平衡条件，求的支座反力如图(b)所示。(b) 取截面I—I右，可求该截面上的单杆AK的轴力（当不利用结构的对称性时，这一步是解题的关键）。计算如下：§5.4截面法与结点法的联合应用 一、桁架的外形对内力的影响桁架的外形对桁架内力的分布有比较大的影响，在设计时应根据这些影响来选择合适的桁架外型。平行弦桁架三角形桁架梯形桁架抛物线形桁架§5.5各式桁架比较 1.桁架的外形对弦杆内力的影响等代梁平行弦桁架，由截面Ⅰ-Ⅰ截断桁架，取左侧部份为隔离体,对结点7取力矩求得§5.5各式桁架比较 FN68的分子相当于此桁架的等代梁上与结点7对应处截面的弯矩M70，分母h则为FN68对矩心的力臂。上式可写为:M0为等代梁上对应截面的弯矩。下弦杆受拉，取正号；上弦受压，取负号。同理，其他弦杆的力可以表示成类似的公式§5.5各式桁架比较 等代梁平行弦桁架,h为常数，弦杆的内力与M0成比例变化。弦杆内力分的规律是：中间弦杆的内力较大而靠近支座处的弦杆内力较小。结论：§5.5各式桁架比较 三角形桁架，力臂h值由两端向中间按直线规律递增，而各结点对应的M0值按抛物线规律变化。力臂的增长比弯矩的增大来得快。弦杆内力变化的是：靠近支座处弦杆的内力较大而逐渐向跨中递减。梯形桁架，其形状介于平行弦桁架和三角形桁架之间，其内力相对比较均匀。抛物线桁架，当计算下弦杆的内力时，M0和h均按抛物线变化。下弦杆的内力为一常数。上弦杆内力的水平分力也相等。整个桁架的上下弦杆的内力分布比较均匀。§5.5各式桁架比较 2.桁架的外形对腹杆（竖杆或斜杆）内力的影响竖杆6-5(或斜杆6-7)的内力可由截面Ⅱ-Ⅱ(或Ⅰ-Ⅰ)以左部份平衡条件∑Y=0求得。竖杆的内力和斜杆内力的竖向分力,分别等于代梁对应结间处的剪力FS0，即§5.5各式桁架比较 由可见：腹杆的内力可正可负，其数值与代梁的剪力有关。靠近支座外腹杆的内力较大，跨中的腹杆内力较小。桁架的弦杆主要是承担弯矩而腹杆则主要承担剪力。问：抛物线形桁架其腹杆的内力为零吗？对于抛物线形桁架由于各结间的下弦杆内力均相等，故可判断其腹杆的内力均为零。上述几种类型的桁架中，抛物线形桁架的内力最为均匀，但构造复杂。在大跨度的结构中采用抛物线型桁架是一种比较合理的选择。§5.5各式桁架比较 二、桁架的应用（1）平行弦桁架有利于标准化，便于制作和施工拼装；适用于轻型桁架，采用一致截面的弦杆而不至于有很大的浪费。（2）三角形桁架符合屋顶构造需要，常在屋架中采用，其端结点构造布置较为困难。（3）抛物线形桁架内力分布均匀，材料使用较为经济，但结点构造复杂，适合于跨度较大的桥梁和屋架。§5.5各式桁架比较 FP如何计算？ 比较内力 组合结构定义：链杆只受轴力，受弯杆件同时受有弯矩和剪力。受力特点：组合结构是指由链杆和受弯杆件混合组成的结构。§5.6组合结构的计算 分析步骤：先求反力，然后计算各链杆轴力，最后分析受弯杆件。选择恰当方法解决关键杆内力计算选择截面时，必须注意区分两类杆求解的关键点:求解此类结构的方法应与求解梁的方法和求解桁架的方法结合应用。§5.6组合结构的计算 例5-3试分析图示组合结构的内力。1）首先求出反力8kN2m2m2m4m4m4mABCDEGF5kNII3kN2）一般情况下应先计算链杆的轴力取隔离体时宜尽量避免截断受弯杆件56-612-656M图(kN.m)FN图(kN)§5.6组合结构的计算 作截面I-I拆开铰C并截断拉杆DE，取右边为隔离体，由∑MC=0有3kN×8m-FNDE×2=0得FNDE=12kN(拉力)分别取结点D、E=>FNFD、FNAD、FNEG、FNEB3）分析受弯杆件取AC杆为隔离体，考虑其平衡可得FCH=12kN(←)，FCV=3kN(↑)绘制内力图§5.6组合结构的计算 例5-4组合结构如图示，试求AC杆的内力图。解:AC杆、CB杆是承受弯曲的杆件。(1)求支座反力,,§5.6组合结构的计算 (2)作截面Ⅰ-Ⅰ，考虑左半部分平衡。由，，得由得由，，得§5.6组合结构的计算 由，，得(3)取铰E为隔离体由，，得§5.6组合结构的计算 (4)作AC杆的内力图。考虑截面Ⅰ-Ⅰ右侧部分平衡，可以作用类似方法和步骤求得CB杆的内力图。§5.6组合结构的计算 思考：取隔离体时,可否用截面Ⅱ-Ⅱ将结构截断？注意：准确判断哪些杆件是梁式杆，哪些杆件是链杆，是计算的关键。§5.6组合结构的计算 例可不求出反力，直接作出受弯杆M图，再由此M图及对称性、结点法求出所有二力杆轴力。§5.6组合结构的计算 5-65-95-115-145-175-19本章课后作业：